физ вопросы. Магнитное поле. Источники магнитного поля. Вектор магнитной индукции. Силовые линии магнитного поля. Поток вектора магнитной индукции. Теорема Гаусса для вектора
 Скачать 3.06 Mb. Скачать 3.06 Mb.
|
|
Магнитное поле. Источники магнитного поля. Вектор магнитной индукции. Силовые линии магнитного поля. Поток вектора магнитной индукции. Теорема Гаусса для вектора 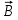 . .Магнитное поле – форма материи, посредством которой в пространстве и времени взаимодействуют движущиеся заряды Магнитное поле порождается движущимися зарядами и действует только на движущиеся заряды 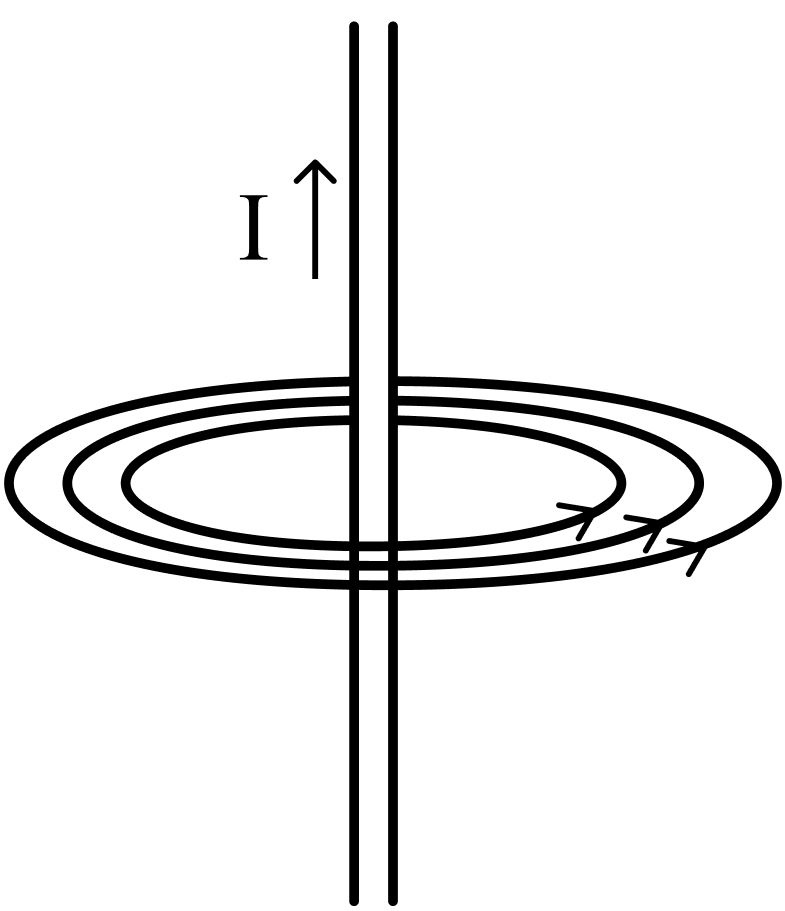 Источники магнитного поля: Движущиеся заряды Проводник с током Переменное во времени электрическое поле Постоянный магнит Вектор магнитной индукции поле в данной точке – векторная величина численно равная силе действующей на 1 метр длины прямолинейного проводника, по которому течет ток 1 ампер если этот проводник расположен перпендикулярно силовым линиям однородного поля 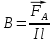 Где B – модуль магнитной индукции[тл] F – сила с которой магнитное поле действует на проводник расположенный перпендикулярно линиям магнитной индукции[н] I – сила тока в проводнике[А] l– длина проводника[м] Вектор магнитной индукции зависит от: Конфигурации проводника с током Величины тока Расположения точки относительно проводника Магнитных свойств среды Магнитное поле является силовыми линиями Свойства линий магнитной индукции: Направление задается правилом винта Всегда замкнуты и охватывают проводник с током Линии не пересекаются Густота линий характеризует вектор 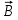 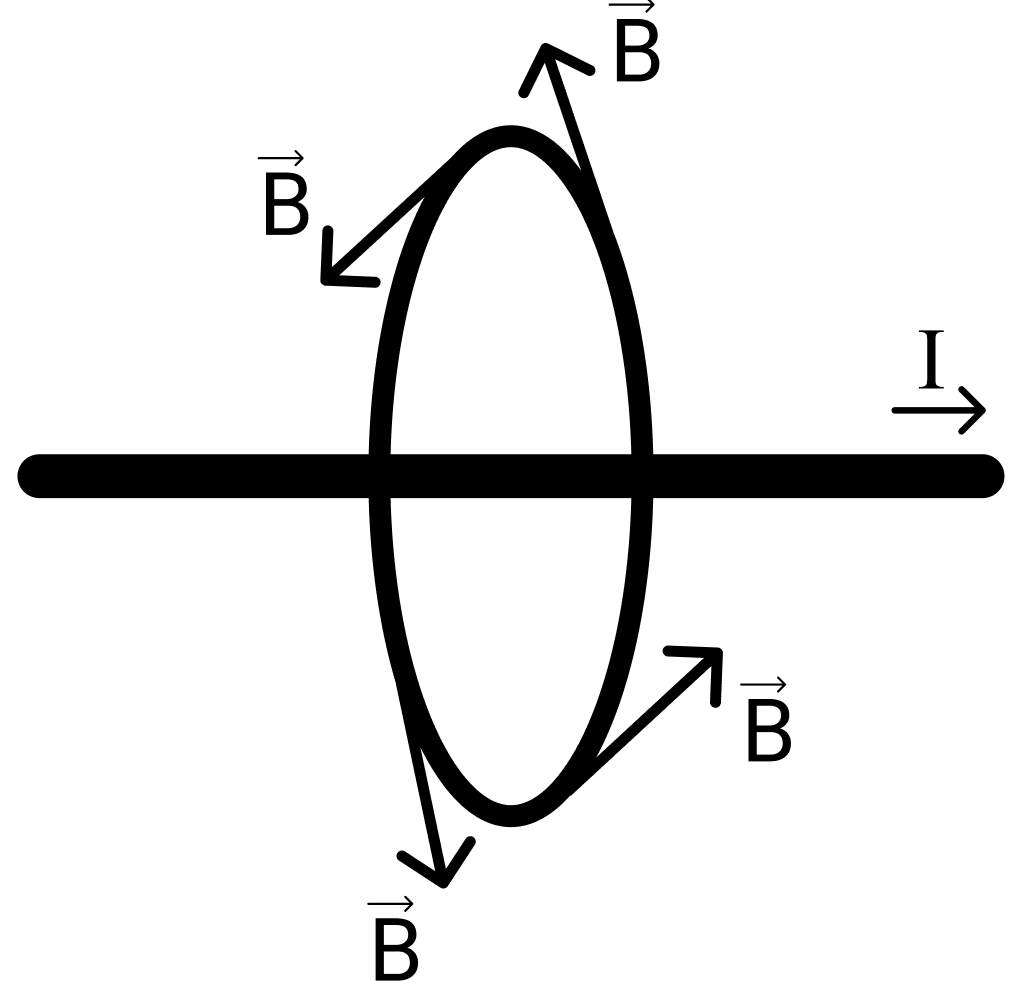 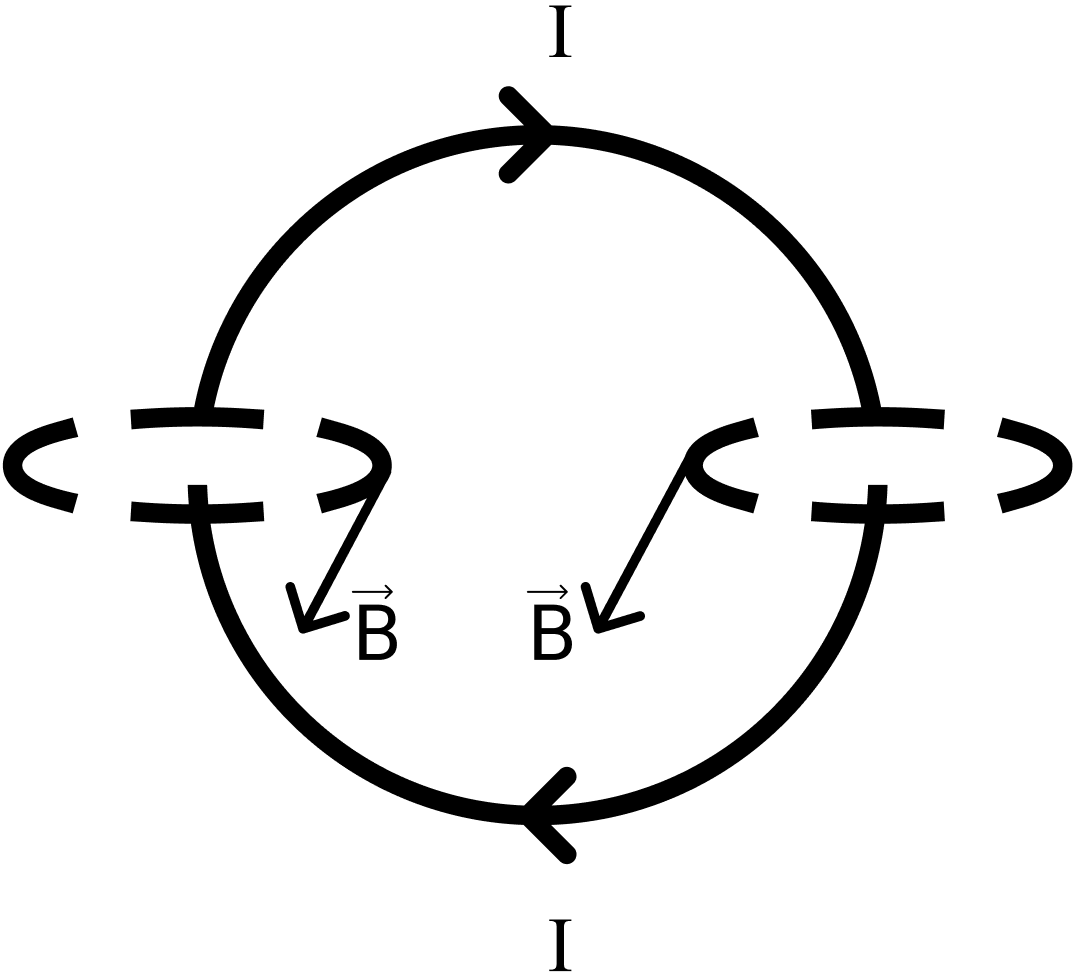 Поток вектора магнитной индукции через площадь dS – скалярная физическая величина числено равная 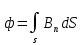 где 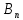 = Bcosα – проекция вектора B на направление нормали к площади dS (α – угол между векторами = Bcosα – проекция вектора B на направление нормали к площади dS (α – угол между векторами 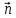 и и 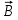 ) ) Силовые линии замкнуты → поток вектора 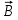 через замкнутую поверхность должен быть равен 0 через замкнутую поверхность должен быть равен 0 Для любого магнитного поля и произвольной замкнутой поверхности S выполняется 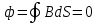 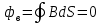 Теорема Гаусса для 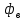 Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю Это математическое выражение говорит, что в природе нет магнитных зарядов источников магнитного поля, на которых начинались и заканчивались линии магнитной индукции Принцип суперпозиции для вектора магнитной индукции. Закон Био-Савара-Лапласа и применение его к расчету магнитных полей: магнитное поле в центре кругового тока (вывод формулы), магнитное поле на оси кругового витка (вывод формулы); магнитное поле отрезка прямого тока (вывод формулы) и бесконечно длинного прямого тока (вывод формулы). Для магнитного поля справедлив принцип суперпозиции. В каждой точке пространства вектор магнитной индукции созданных в этой точке всеми источниками магнитных полей равен векторной сумме векторов магнитных индукций, созданных в этой точке всеми источниками магнитных полей: 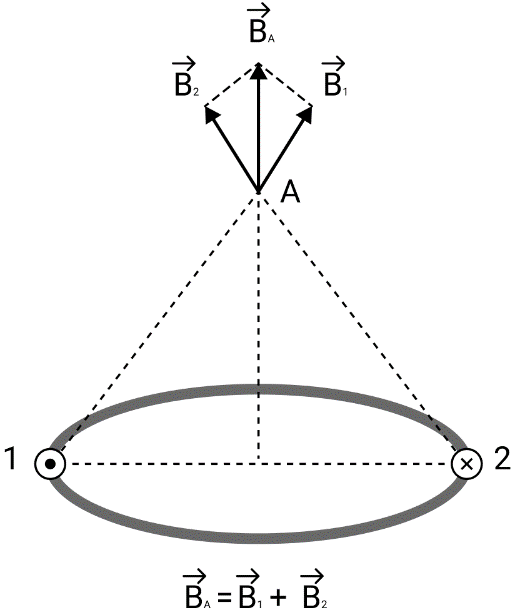 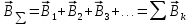 Закон Био – Савара – Лапласа М 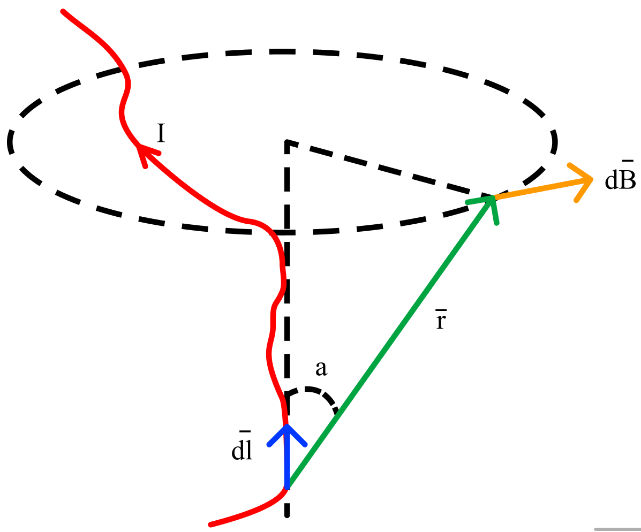 агнитное поле от любого тока можно определить как векторную сумму полей, которые создаются отдельными элементарными участками тока. агнитное поле от любого тока можно определить как векторную сумму полей, которые создаются отдельными элементарными участками тока. 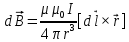 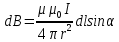 Закон Био – Савара – Лапласа в центре кругового тока В 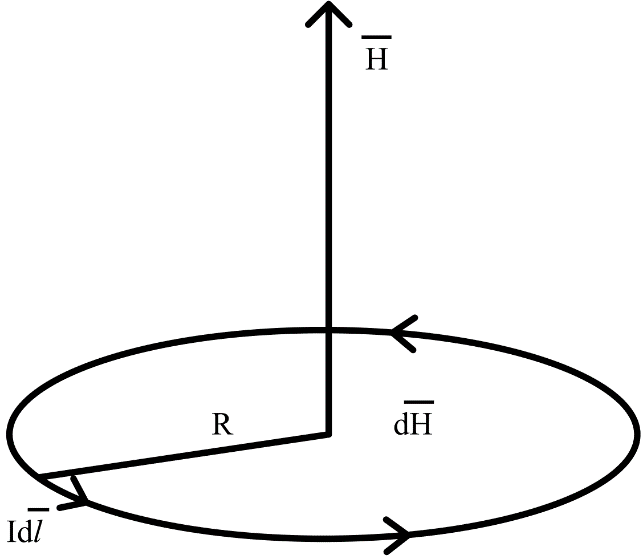 данном случае имеем согласно закону данном случае имеем согласно закону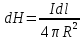 Откуда находим после интегрирование по всей длине витка – окружности радиуса 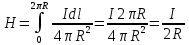 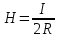 Закон Био – Савара – Лапласа на оси кругового витка 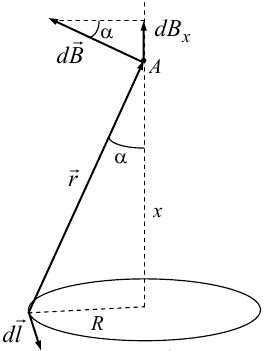 Пусть электрический ток силой I течет по проводнику радиусом R. Пусть электрический ток силой I течет по проводнику радиусом R.Возьмем на оси кругового витка точку А, отстоящую от плоскости витка на расстоянии х. Выберем ось х вдоль оси витка. Выделим на витке с током элемент тока dl. Очевидно, что при суммировании векторов dB от всех элементов витка горизонтальные составляющие векторов dB взаимно компенсируются, а вертикальные составляющие (dBx) складываются скалярно. Тогда индукция магнитного поля в точке А будет 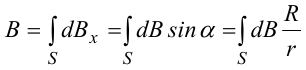 здесь S − длина витка, R − его радиус. Согласно закону Био-Савара-Лапласа 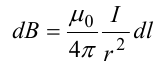 (угол между векторами r и dl равен π/2). Окончательно 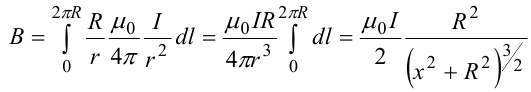 Закон Био – Савара – Лапласа магнитное поле прямого тока и бесконечного проводника с током Р 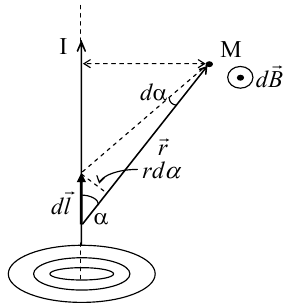 ассчитаем, используя закон Био-Савара-Лапласа, магнитное поле, создаваемое бесконечным прямым проводником с током, в точке М, отстоящей на расстоянии а от проводника. ассчитаем, используя закон Био-Савара-Лапласа, магнитное поле, создаваемое бесконечным прямым проводником с током, в точке М, отстоящей на расстоянии а от проводника.Выделим элемент проводника dl. Пусть элемент dl виден из точки М под малым углом dα. Положение точки М относительно элемента dl определяется вектором r. Из рис. видно, что выполняются следующие соотношения 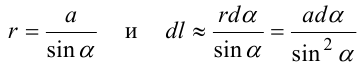 Используя закон Био-Савара-Лапласа, запишем индукцию магнитного поля, создаваемого элементом тока dl в точке М 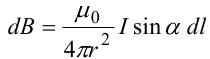 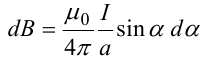 Для того, чтобы найти индукцию магнитного поля, создаваемого всем проводом, нужно, используя принцип суперпозиции, найти сумму векторов dBi от всех элементов dli. 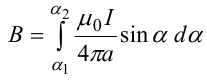 В случае бесконечного прямого тока α1=0 и α2=π, тогда 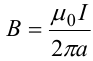 В общем случае индукция магнитного поля, создаваемого прямым проводником с ток конечной длины равна 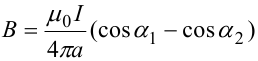 Теорема о циркуляции вектора магнитной индукции. Магнитное поле соленоида (вывод формулы). Магнитное поле внутри и снаружи проводника с током (вывод формулы). Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур. ток берется со знаком + если направление линии этого тока совпадает с направлением обхода. в противном случае берется со знаком - Расчет магнитного поля соленоида 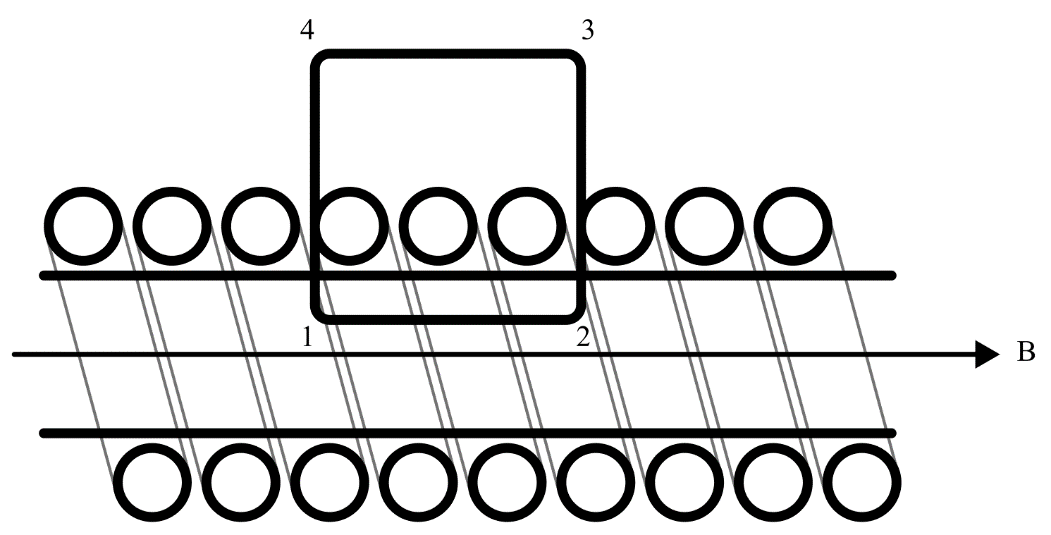 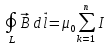 Веток магнитной индукции имеет отличную от нуля проекции только на стороне обхода 1-2 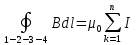 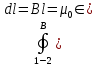 ⇓ 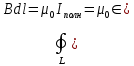 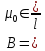 Магнитное поле внутри и снаружи проводника 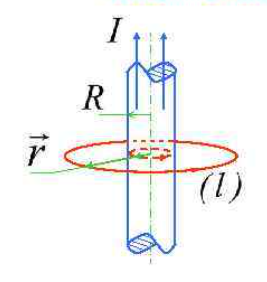 В равноудаленных точках от оси поле одинаково В равноудаленных точках от оси поле одинаково 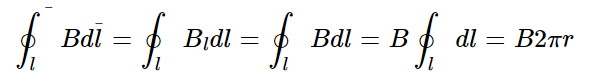 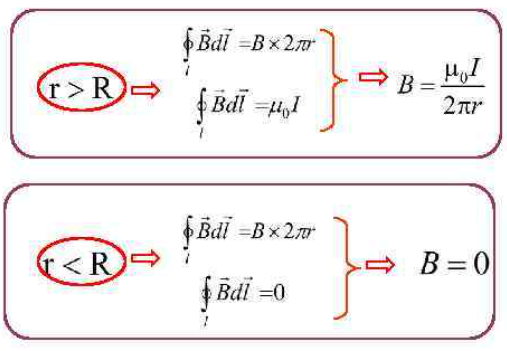 Сила Ампера. Сила Лоренца. Движение заряженной частицы в однородном магнитном поле. Вычисление параметров винтовой траектории. Эффект Холла. Сила ампера модуль силы, с которой магнитное поле действует на находящийся в нем прямолинейный проводник с током, равен произведению индукции. В этом поле, силы тока I, длины участка проводника l и синуса угла между направлениями тока и индукции магнитного поля. Сила Ампера если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора индукции магнитного поля входила в ладонь, а четыре вытянутых пальца указывали направление тока, то отогнутый на 90° большой палец укажет направление силы Ампера. Магнитное взаимодействие проводников с током используется для определения в СИ одной из основных единиц — единицы силы тока — ампера. Один ампер есть сила постоянного тока, поддерживаемого в каждом из двух прямолинейных параллельных проводниках бесконечной длины и ничтожно малого кругового сечения, расположенных на расстоянии 1 м один от другого в вакууме, который вызывает между этими проводниками силу взаимодействия, равную Сила Ампера пропорциональна силе тока в проводнике. Сила Ампера пропорциональна длине активной части проводника. Сила Лоренца Силой действующая в магнитном поле на движущийся заряд называется силой Лоренца 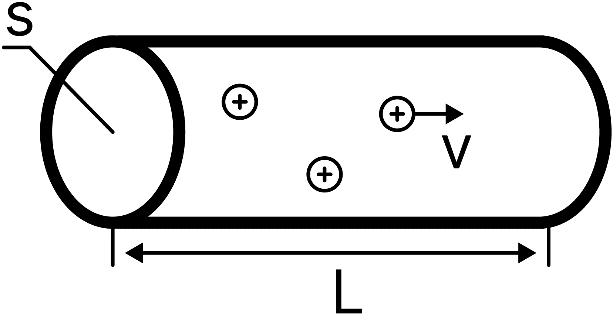 L – длина L – длинаS – площадь сечения проводника I – const N – число электронов проводимости 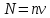 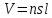 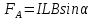 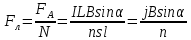 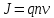 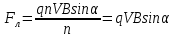 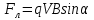 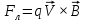 Где 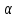 угол между угол между 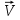 и и 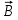 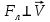 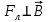 Направление силы Лоренца определяется по правилу левой руки если левую руку расположить так, чтобы перпендикулярная к скорости 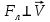 следовательно сила Лоренца не совершает работу и не изменяет кинетическую энергию, а изменяет только направление движения заряженной частицы. следовательно сила Лоренца не совершает работу и не изменяет кинетическую энергию, а изменяет только направление движения заряженной частицы. 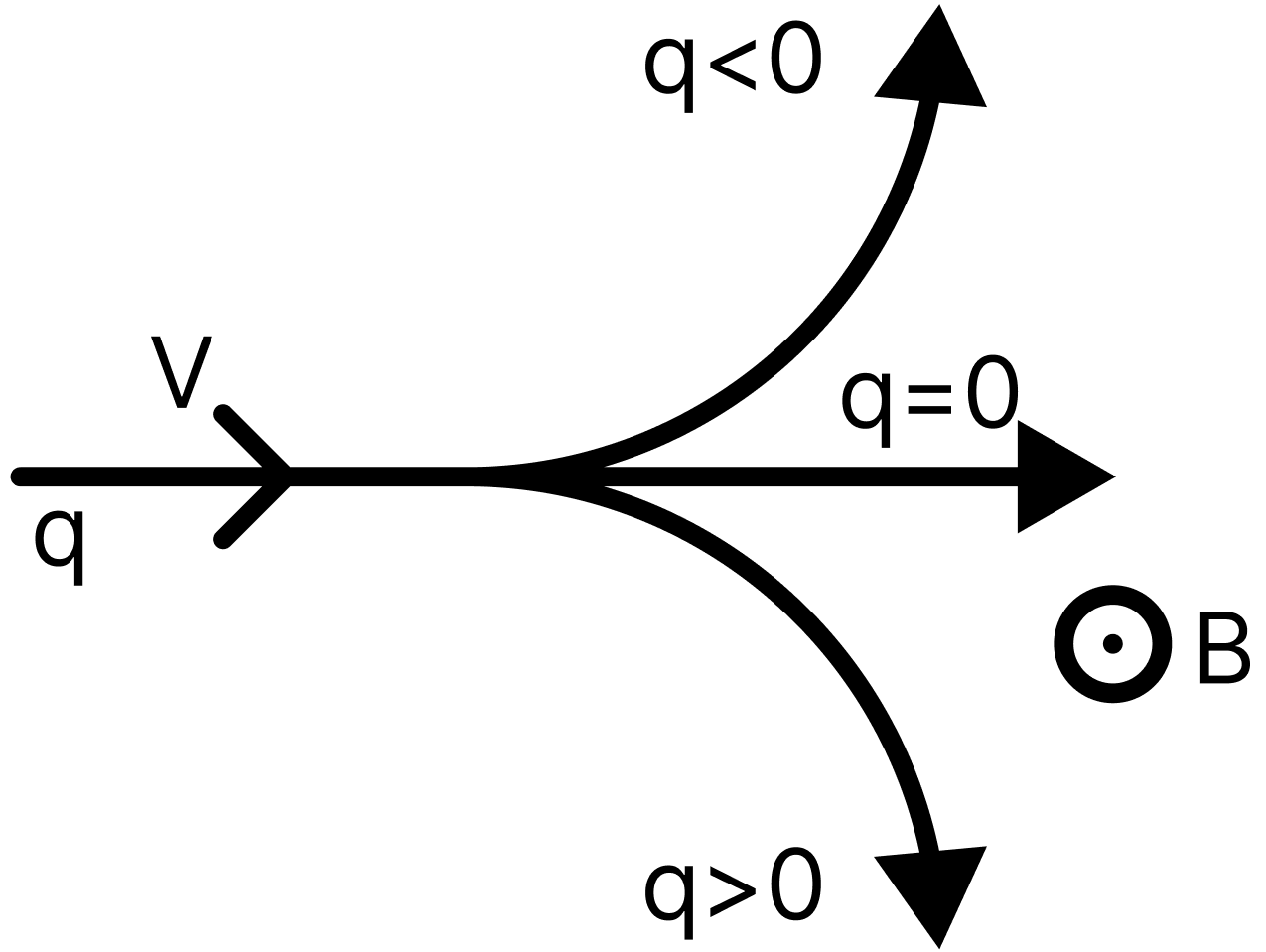 Вычисление параметров винтовой траектории Ускорение частицы и радиус окружности описываемой частицей в магнитном поле. 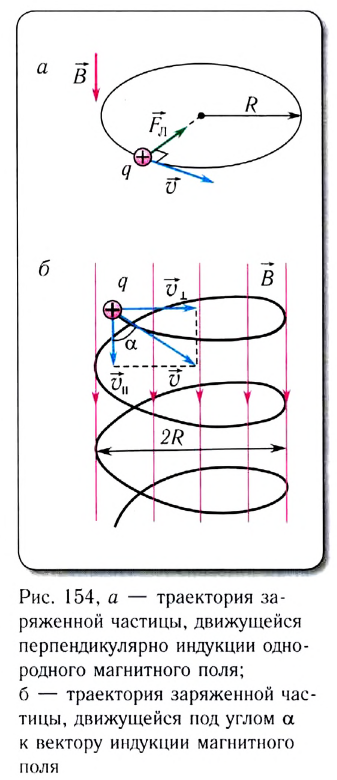 Если скорость направлена под углом к индукции магнитного поля, движение заряда можно представить в виде двух независимых движений равномерного вдоль поля со скоростью по окружности радиусом R в плоскости, перпендикулярной к вектору В результате сложения обоих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю Период этого движения определяется по формуле Шаг спирали 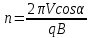 |
