контрольна. Магнитное поле. Закон БиоСавараЛапласа
 Скачать 259.98 Kb. Скачать 259.98 Kb.
|
|
Контрольная работа №3 Сорокин Виталий Сергеевич, учебный шифр: 67п-38 Тема: магнитное поле. Закон Био-Савара-Лапласа. 8. По проводнику, согнутому в виде квадратной рамки со стороной a = 10 см, течёт ток силой 5 A. Определить магнитную индукцию поля в точке, равноудалённой от вершины квадрата на расстояние, равное длине его стороны. Дано: 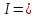 5 А, 5 А, 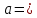 10 см = 0,1 м, 10 см = 0,1 м, 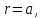 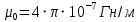 Найти: 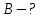 Решение: Условно разбиваем проводник на четыре проводника, каждый из которых создает магнитное поле. Результирующая магнитная индукция 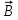 в точке в точке 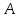 является векторной суммой индукций является векторной суммой индукций 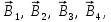 создаваемых в этой точке токами, текущими в каждом из четырех проводов, являющихся сторонами квадрата, т.е. создаваемых в этой точке токами, текущими в каждом из четырех проводов, являющихся сторонами квадрата, т.е. 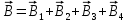 . .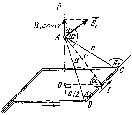 На рисунке изображен только один из четырех векторов 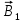 , соответствующий полю, создаваемому током в проводе DС. Направления векторов индукции, определенны по правилу правой руки. Вектор , соответствующий полю, создаваемому током в проводе DС. Направления векторов индукции, определенны по правилу правой руки. Вектор 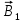 перпендикулярен плоскости треугольника АДС. перпендикулярен плоскости треугольника АДС.Все вектора 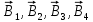 расположены на одном расстоянии от точки O, по ним протекает один и тот же ток, и у них одинаковая длинна. расположены на одном расстоянии от точки O, по ним протекает один и тот же ток, и у них одинаковая длинна.Результирующий вектор 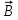 будет направлен вдоль оси ОО и равен сумме проекций всех векторов на направление этой оси: будет направлен вдоль оси ОО и равен сумме проекций всех векторов на направление этой оси: 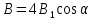 . . Из рисунка следует, что 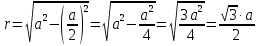 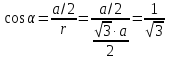 Тогда 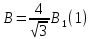 Магнитная индукция поля, создаваемого отрезком проводника, выражается формулой 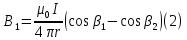 где I – сила тока в проводнике; r – расстояние от проводника до точки поля, в которой надо определить магнитную индукцию; 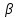 1 и 1 и 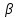 2 – углы, образованные направлением тока в проводнике и радиус – векторами, проведенными от концов проводника к точке А. 2 – углы, образованные направлением тока в проводнике и радиус – векторами, проведенными от концов проводника к точке А.Из рисунка 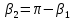 , следовательно, , следовательно, 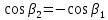 и выражение (2) приобретает вид и выражение (2) приобретает вид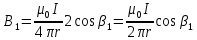 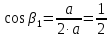 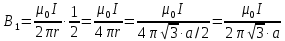 Подставляем это выражение В1 в формулу (1) и заменяем r: 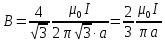 Подставим значения и вычислим 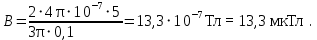 Ответ: 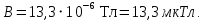 Тема: сила Ампера 18. Определить вращающий момент плоского контура площадью 0,08 м2, помещенного в однородное магнитное поле с индукцией 20 Тл, если по контуру течет ток 10 А, а плоскость контура составляет с линиями индукции угол 30°. Дано: 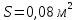 , В = 20 Тл, , В = 20 Тл, 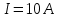 , , 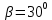 Найти: 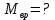 Решение: На контур, ось которой составляет угол β с линиями поля и по которому идет ток I, действует момент сил 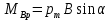 , где , где pm – магнитный момент плоского контура с током, 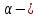 угол между линиями магнитной индукции однородного поля и нормалью угол между линиями магнитной индукции однородного поля и нормалью 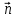 к площади квадрата: к площади квадрата: 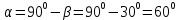 . . Магнитный момент контура равен по определению 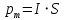 , где , где 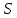 – площадь рамки. – площадь рамки.Тогда магнитный момент силы, действующей на круглую рамку 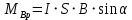 . .Подставим значения и вычислим 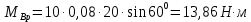 Ответ: 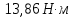 Тема: работа в магнитном поле. 28. Круговой виток с током 0.2 А свободно установился в магнитном поле с индукцией 0.4 Тл и затем его повернули на 45о, совершив работу 0.2 Дж. Чему равен радиус витка? Дано: I = 0,2А, 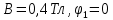 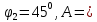 0,2 Дж 0,2 ДжНайти: R -? Решение: 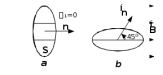 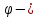 угол между угол между 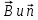 . .a) плоскость рамки перпендикулярна силовым линиям поля: 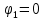 b) виток, повернули: 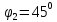 Работа внешних сил, по перемещению контура с током в магнитном поле, равна произведению силы тока в контуре на изменение магнитного потока, пронизывающего контур, взятого со знаком минус: 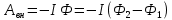 Работа отрицательная т.к. ее совершают над контуром. где 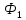 - магнитный поток, пронизывающий контур до поворота; - магнитный поток, пронизывающий контур до поворота; 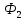 - магнитный поток, пронизывающий контур, после поворота. - магнитный поток, пронизывающий контур, после поворота.Работа внешних сил поля 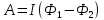 Магнитный поток, пронизывающий контур 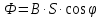 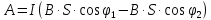 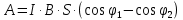 Площадь витка 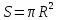 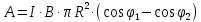 Радиус витка 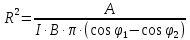 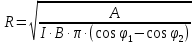 Подставим значения и вычислим 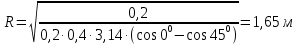 Ответ: 1,65 м Тема: заряженная частица в магнитном поле, сила Лоренца. 38. Протон со скоростью 2 · 106 м/с влетает в область, где включены и магнитное и электрическое поле. Магнитное поле с индукцией В = 0.4 Тл перпендикулярно скорости частицы. Чему равно и куда направлена напряженность электрического поля, если протон продолжает двигаться прямолинейно и равномерно? Дано: 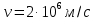 , В = 0,4 , В = 0,4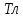 Найти: Е-? Решение. В скрещенных электрическом и магнитных полях на частицу действует две силы: сила Лоренца, направленная перпендикулярно скорости 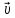 и вектору магнитной индукции и вектору магнитной индукции 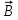 : : 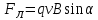 Кулоновская сила с боку электрического поля совпадает с вектором напряженности, т. к. заряд 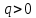 . . 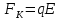 Так как протон продолжает двигаться прямолинейно и равномерно, то согласно второму закона Ньютона, он движется без ускорения и 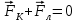 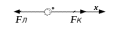 Спроектируем полученное уравнение на ось х, получим 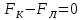 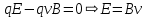 Подставим значения и вычислим: 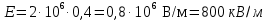 Ответ: 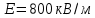 Тема: закон полного тока. 48. Соленоид длиной 1 м и сечением S= 16 см2 содержит N=2000 витков. Вычислить потокосцепление 𝜓 при силе тока в обмотке 10 А, используя закон полного тока. Дано: l = 1 м, S = 16 см2 = 16 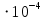 см2, N=2000, I = 10 А см2, N=2000, I = 10 АНайти: 𝜓 - ? Решение: Катушка представляет собой систему одинаковых круговых токов с общей прямой осью. Магнитное поле, созданное каждым витком в отдельности, складывается. 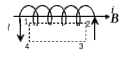 Направление вектора магнитной индукции, по правилу буравчика, может быть только параллельным оси катушки как вне, так и внутри неё. Выберем контур для применения теоремы о циркуляции в виде прямоугольника, две стороны которого располагаются вдоль оси катушки, а две другие – перпендикулярно. Одна из сторон при этом расположена внутри катушки, а противоположная – вне. Циркуляция вектора В складывается из интегралов: 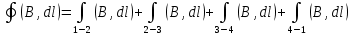 . .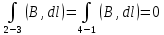 Так как на любом участке сторон контура 23 и 41 векторы 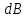 и и 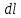 взаимно-перпендикулярны. взаимно-перпендикулярны. Участок 34 может быть выбран на любом расстоянии от оси соленоида, в частности на очень большом, где магнитное поле пренебрежимо. Поэтому выражение для циркуляции практически полностью определяется индукцией поля внутри соленоида. Применим теорему о циркуляции: циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром: 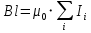 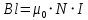 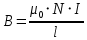 Потокосцепление контура: 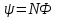 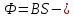 магнитный поток, где S – площадь поперечного сечения катушки магнитный поток, где S – площадь поперечного сечения катушки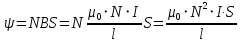 Подставим значения и вычислим: 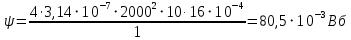 Ответ: 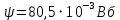 Тема: закон Фарадея, электромагнитная индукция. 58. Проводящий круговой виток радиусом a=10 см вращается в однородном магнитном поле, индукция которого В=0,02Тл, так, что угол между нормалью к его плоскости и вектором В изменяется по закону α=πt (t – время в секундах). Какое количество теплоты выделяется в витке за промежуток времени от 0 до 5 с, если его сопротивление R=5Ом. Дано: a=10 см = 0,1 м, В=0,02Тл, α=πt, R=5Ом Найти: Q -? Решение: При вращении витка в магнитном поле изменяется магнитный поток, а значит, возникает индукционный ток. Величину индукционного тока I, текущего в контуре, найдем по закону Ома для полной цепи.  где εi - ЭДС индукции, R - сопротивление витка. Количество теплоты, выделившуюся на витке, определим по закону Джоуля – Ленца. Закон Джоуля – Ленца в виде  – справедлив только для постоянного тока (I = const). Если же сила тока меняется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде – справедлив только для постоянного тока (I = const). Если же сила тока меняется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде Для определения теплоты, выделившейся за конечный промежуток времени, выражение надо проинтегрировать в пределах от t1 до t2:  Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в контуре при изменении магнитного потока, пересекающего этот контур, равна по модулю скорости изменения магнитного потока. 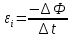 Магнитный поток 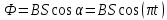 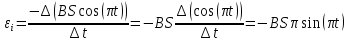 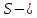 площадь сечения: площадь сечения: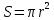 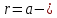 радиус витка соленоида. радиус витка соленоида.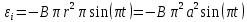 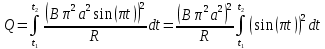    Подставим значения и вычислим:  Ответ:1,95 мкДж Тема: электромагнитные колебания и волны. 68. Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите: сколько раз энергия конденсатора достигает максимального значения в период от нуля до 2мкс? Сколько раз энергия катушки достигает наибольшего значения от нуля до 2 мкс? По графику определите амплитуду колебаний напряжений, период колебаний, циклическую частоту, линейную частоту. Напишите уравнение зависимости напряжения от времени.  Найти:  Решение: 1) На графике изображена косинусоида. Уравнение зависимости напряжения от времени:   – мгновенное значение напряжения; – мгновенное значение напряжения; 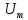 - амплитуда колебаний (модуль максимального значения напряжения); - амплитуда колебаний (модуль максимального значения напряжения);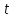 – время; – время; 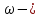 циклическая частота. циклическая частота. По графику определяем: 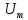 = 2 мВ = = 2 мВ = 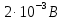 , Т = 2мкс= , Т = 2мкс=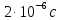 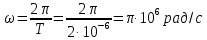 Частота: 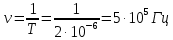 Уравнение зависимости напряжения от времени 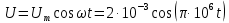 2) Энергия на конденсаторе в колебательном контуре максимальна в те моменты времени, когда напряжение на конденсаторе максимально. По графику напряжение максимально и принимает значения 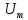 = 2 мВ в моменты времени 0мкс и 2мкс. = 2 мВ в моменты времени 0мкс и 2мкс. Значит, энергия конденсатора максимальная 2 раза за 2мкс. 3) Энергия катушки достигает максимального значения в те моменты времени, когда сила тока принимает максимальное значение, напряжение на конденсаторе при этом равно нулю. По графику напряжение минимально и принимает значения 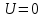 в моменты времени: 0,5мкс и 1,5мкс. в моменты времени: 0,5мкс и 1,5мкс. Значит, энергия катушки максимальная 2 раза за 2мкс. Ответ: 2; 2; 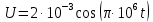 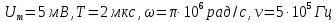 |
