Информатика 11 класс, задача на оптимизацию. ЗАДАЧА на оптимизацию. Максимальный спрос
 Скачать 383.16 Kb. Скачать 383.16 Kb.
|
|
ЗАДАЧА №2 Вариант № 7 Завод может производить четыре вида изделий А, В, С и D. По технологии каждое изделие обрабатывается четырьмя машинами (время обработки в минутах в пересчете на один килограмм готовой продукции показано в таблице). Каждая машина может работать 60 часов в неделю. Изделия могут продаваться по следующим ценам: А–9$, B–7$, C–6$, D–5$ за кг. Переменные затраты на оплату труда составляют 2$ в час для машин 1 и 2 и 3$ для машин 3 и 4. Материальные затраты составляют 4$ на каждый кг. продукции А и 1$ на каждый кг. продукции В, С и D. Определить оптимальный план производства, максимизирующий прибыль при заданном максимальном спросе для каждого вида продукции. Решение. ПОСТАНОВКА ЗАДАЧИ Завод производит изделия n (4) видов при этом используя машины m (4) типов. Расход времени каждого типа машин на производство изделий представлен таблицей 1:
Рыночная цена изделий составляет 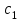 (9) д.е., (9) д.е., 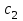 (7) д.е., (7) д.е., 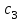 (6) д.е., (6) д.е., 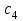 (5) д.е.. (ячейки G7:G10) (5) д.е.. (ячейки G7:G10)Ai -материальные затраты на кг продукции (ячейкиH7:H10) Определить оптимальный план производства, максимизирующий прибыль при заданном максимальном спросе для каждого вида продукции. Экономико-математическая модель. Исходя из условия, делается вывод о том, что эта задача является задачей линейного программирования. Обозначим за неизвестные переменные 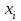 (i =1….4) – ячейки A17:D17 - объем производства соответствующих изделий. (i =1….4) – ячейки A17:D17 - объем производства соответствующих изделий.Значения таблицы 1 представляют собой матрицу с коэффициентами (bij). Где i – номер строки, j – номер столбца С 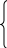 истема ограничений по времени (в минутах) имеет вид: истема ограничений по времени (в минутах) имеет вид:5  х1+3х2+4х3+4х4<=3600 x1<=400 х1+3х2+4х3+4х4<=3600 x1<=40010x1+6x2+5x3+2x4<=3600 x2<=100 6x1+4x2+3x3+x4 <=3600 x3<=150 3x1+8x2+3x3+2x4<= 3600, x4<=500 Дополнительные ограничения xi>=0, где i=1,2,3,4 ; F- выручка от реализации, F= cixi , где i=1,2,3,4 G – затраты, G= AiXi + BijXi P  – прибыль, P=F-G max – прибыль, P=F-G maxРешение задачи в EXCEL: Формулы экранной формы задачи
Ограничения и граничные условия задачи 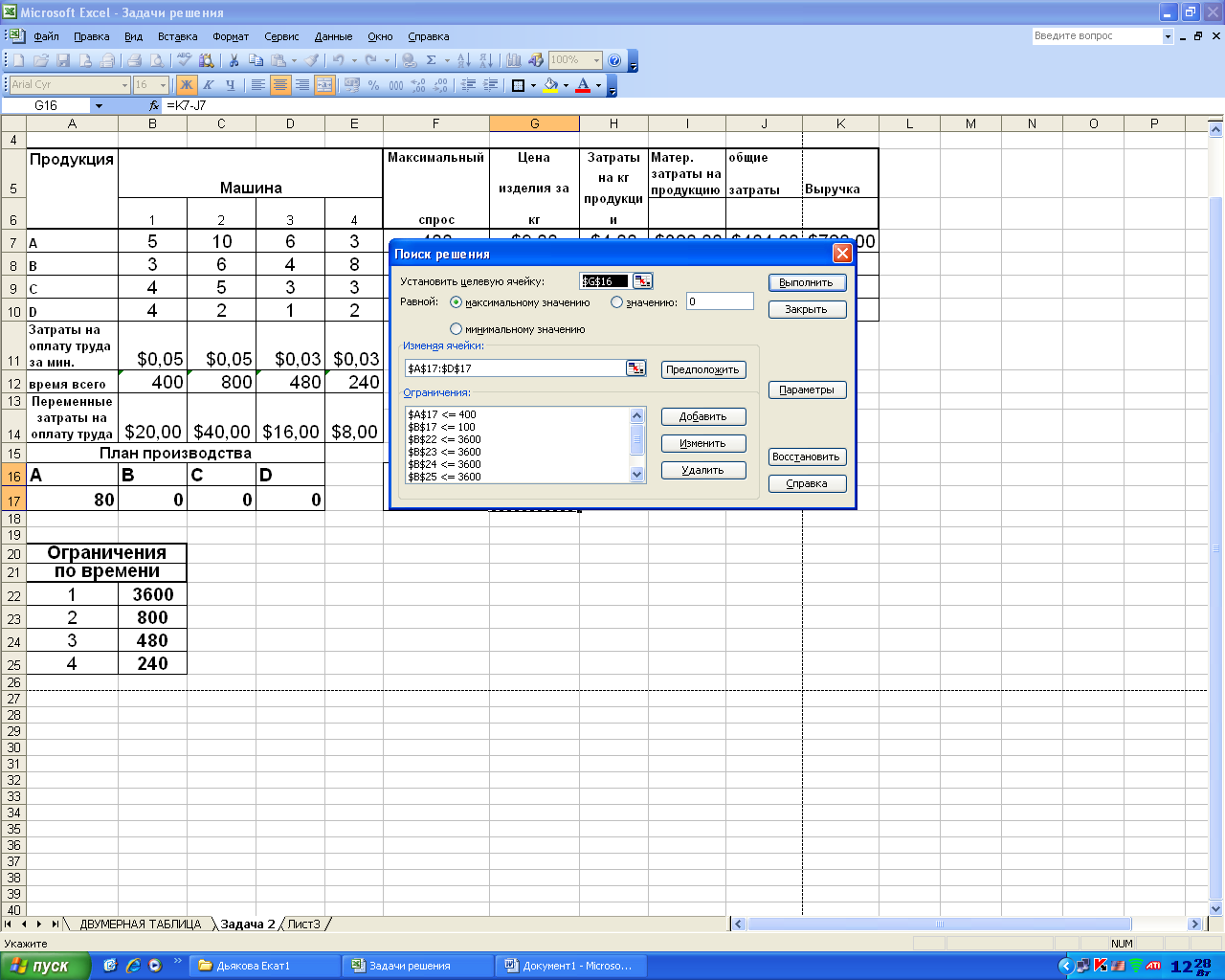 В окне «Параметры» установить«Линейная модель» Результаты решения задачи: 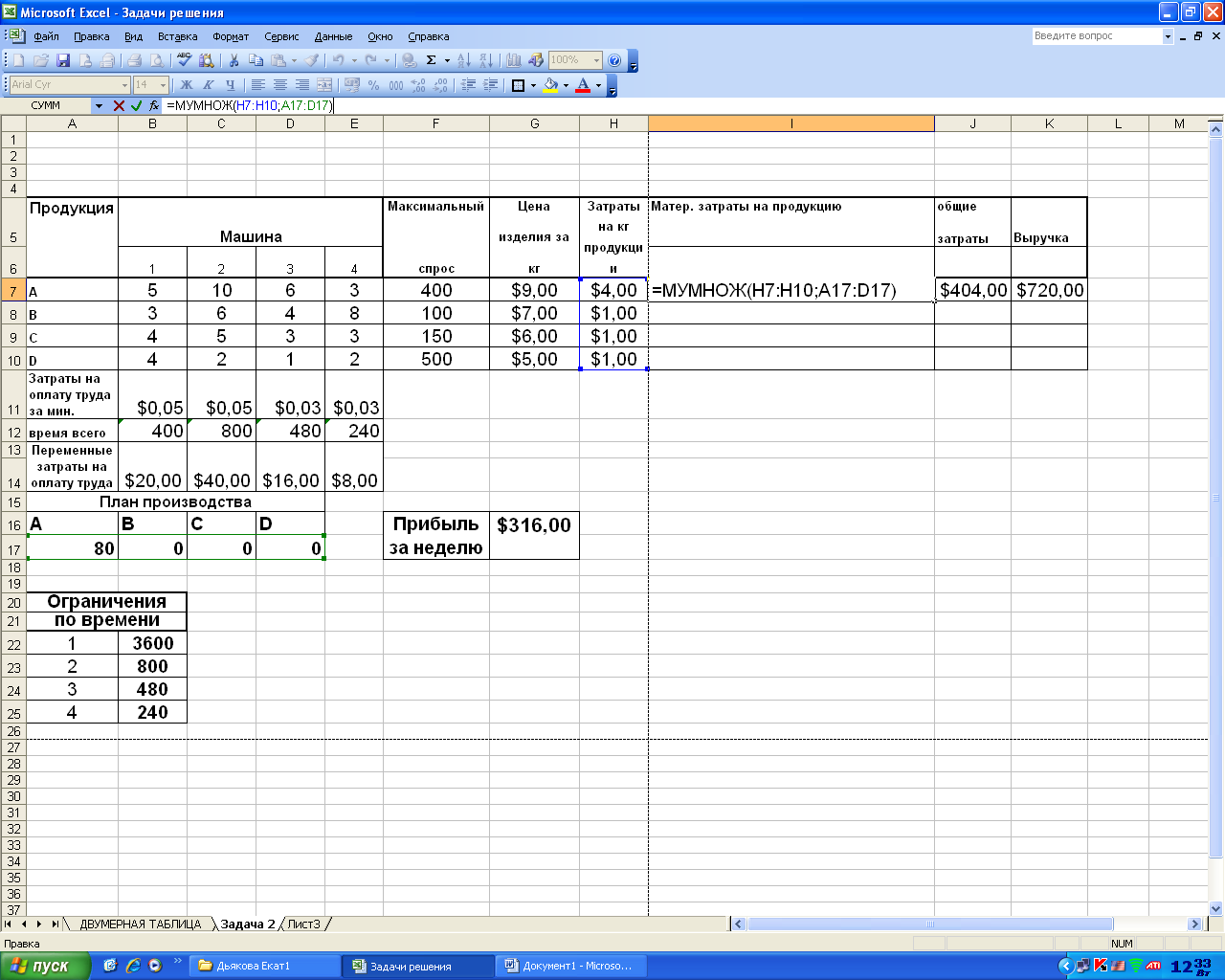 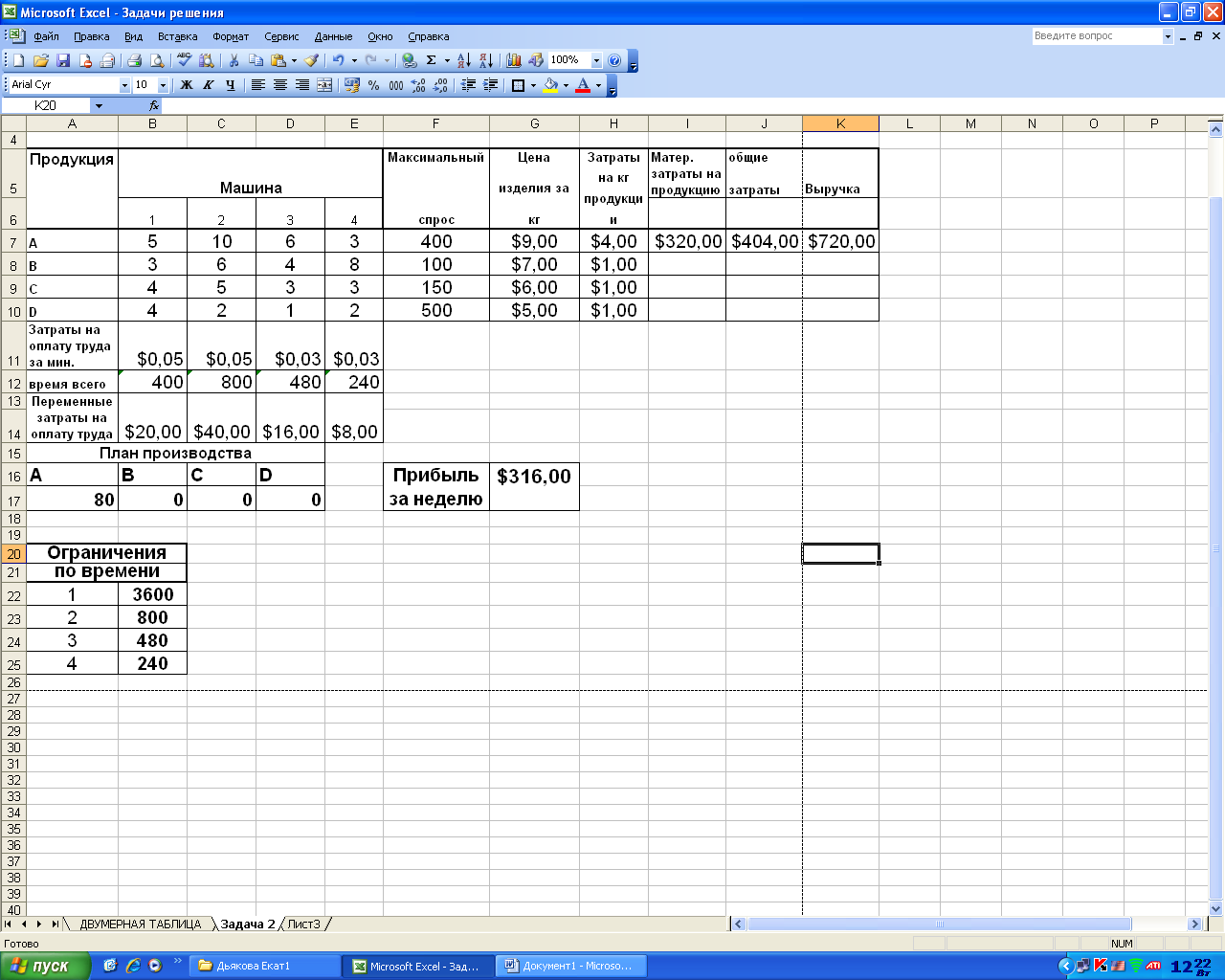 ВЫВОД: | |||||||||||||||||||||||||||||||||||||||||||||||
