анализ. Маннобоева Гулхае 10. Сглаживание методом простой скользящей средней
 Скачать 140.59 Kb. Скачать 140.59 Kb.
|
|
Маннобоева Гулхае 10.Сглаживание методом простой скользящей средней Сглаживание – это способ, обеспечивающий быстрое реагирование прогноза на все события, происходящие в течение периода протяженности базовой линии. Простая скользящая средняя – пример расчета по трем точкам: Простая скользящая средняя Скользящая средняя взвешенная – пример расчета по трем точкам: Скользящая средняя взвешенная Алгоритм сглаживания методом скользящей средней Для временного ряда y1,y2,...,yn определяется интервал сглаживания m (m < n). Если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания берут по возможности большим; интервал сглаживания уменьшают, если нужно сохранить более мелкие колебания. При прочих равны условиях интервал сглаживания рекомендуют брать нечетным. Для первых m уровней временного ряда вычисляется их средняя арифметическая; это будет сглаженное значение уровня ряда, находящегося в середине интервала сглаживания. Затем интервал сглаживания сдвигается на один уровень вправо, повторяется вычисление средней арифметической и т.д. Для вычисления сглаженных уровней ряда у применяется формула: В результате такой процедуры получаются n - m + 1 сглаженных значений уровня ряда. Недостатки метода Первые и последние уровни ряда теряются (не сглаживаются). Метод применим лишь для рядов, имеющих линейную тенденцию. ПРИМЕР. Произвести сглаживание ряда динамики трехквартальной скользящей средней. Решение.
ПРИМЕР №2. Произвести сглаживание ряда динамики трехлетней скользящей средней. Изобразить фактический и выровненный ряды графически. Сделать выводы. Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
Решение было получено и оформлено с помощью сервиса: Сглаживание методом скользящей средней Вместе с этой задачей решают также: Аналитическое выравнивание Уравнение парной линейной регрессии Уравнение множественной регрессии Показатели вариации Показатели динамики Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
16.Применение кривых роста Применение моделей кривых роста в прогнозировании. Удобным средством описания одномерных временных рядов является их выравнивание с помощью тех или иных функций времени (кривых роста). Кривая роста позволяет получить выравненные или теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае полного совпадения динамики явления с кривой. Процедура разработки прогноза с использованием кривых роста включает в себя следующие этапы: 1.Выбор одного или нескольких кривых, форма которых соответствует характеру изменения временных рядов. 2.Оценка параметров выбранных кривых. 3.Проверка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой роста 4. Расчет точечного и интервального прогнозов. 5.Оценка прогноза. Кривые роста могут быть разделены на 3 класса. К первому классу относятся функции, используемые для описания процессов с монотонным характером развития и отсутствием пределов роста. Ко 2 классу относятся кривые, описывающие процесс, который имеет предел роста в исследуемом периоде. Эти функции называются кривыми насыщения. Если кривые насыщения имеют точку перегиба, то они относятся к 3 классу - к S-образным кривым. Эти кривые описывают как бы два последовательных процесса, когда прирост зависит уже от достигнутого уровня. Причем один развивается с ускорением, другой - с замедлением. Среди кривых роста 1-го класса выделяют класс полиномов: Yt=a0+a1t+a2t+…aptp ao…p – параметры (коэффициенты) полинома. t – время. Параметры полиномов невысоких степеней могут иметь конкретную интерпретацию в зависимости от содержания временного ряда. Например, параметр а0 - это начальный уровень ряда при t=0. Параметр а1 можно трактовать как скорость роста, а2 как ускорение роста. Полином первой степени - это прямая: Yt=a0+a1t Основные свойства тренда в форме прямой: 1) равные изменения за равные промежутки времени (цепные приросты = изменению); 2)если средний абсолютный прирост – положительная величина, то относительные приросты (темпы прироста) постепенно уменьшаются; 3)если средние абсолютные изменения – отрицательная величина, то относительные изменения постепенно увеличиваются по абсолютной величине снижения к предыдущему уровню; 4) если имеется тенденция к сокращению уровней, а изучаемая величина является по определению положительной, то среднее значение параметра а1 не может быть больше среднего уровня (т.е. «а0»); 5) при линейном тренде ускорение (т.е. разность абсолютных значений за последовательные периоды)=0 Полином 2-ой степени: Yt=a0+a1t+a2t2 Парабола применяется в тех случаях, когда процесс развивается равноускоренно. Параболический тренд обладает следующими свойствами: 1)неравные, но равномерно возрастающие или убывающие абсолютные изменения за равные промежутки времени; 2)поскольку а0 как правило величина положительная, то характер тренда определяется знаками параметров а1 и а2. При а1>0 и а2>0 имеем восходящую ветвь, т.е. тенденцию с ускоренному росту уровней. При а1<0 и а2<0 имеем нисходящую ветвь, т.е. тенденцию к ускоренному сокращению уровней. При а1>0 и а2<0 имеем либо восходящую ветвь с замедляющимся ростом уровней, либо обе ветви параболы, если их по существу можно считать единым процессом. При а1<0 и а2>0 имеем либо нисходящую ветвь с замедляющимся сокращением уровней, либо обе ветви, если их можно считать единым процессом. 3) В зависимости от соотношения между параметрами, цепные темпы изменений могут либо уменьшаться, либо некоторое время увеличиваться. Но при достаточно длительном периоде темпы роста начинают изменяться, а темпы сокращения уровней начинают возрастать. Полином 3-й степени: Yt=a0+a1t+a2t2+a3t3 У этого полинома знак прироста ординат может изменяться 1 или 2 раза. Отличительная черта полиномов – отсутствие в явном виде зависимости приростов от значений ординат. Нахождение параметров полиномов определяется методом наименьших квадратов. С учетом переноса начала координат в середину ряда параметры для уравнения прямой определяются по следующему алгоритму: 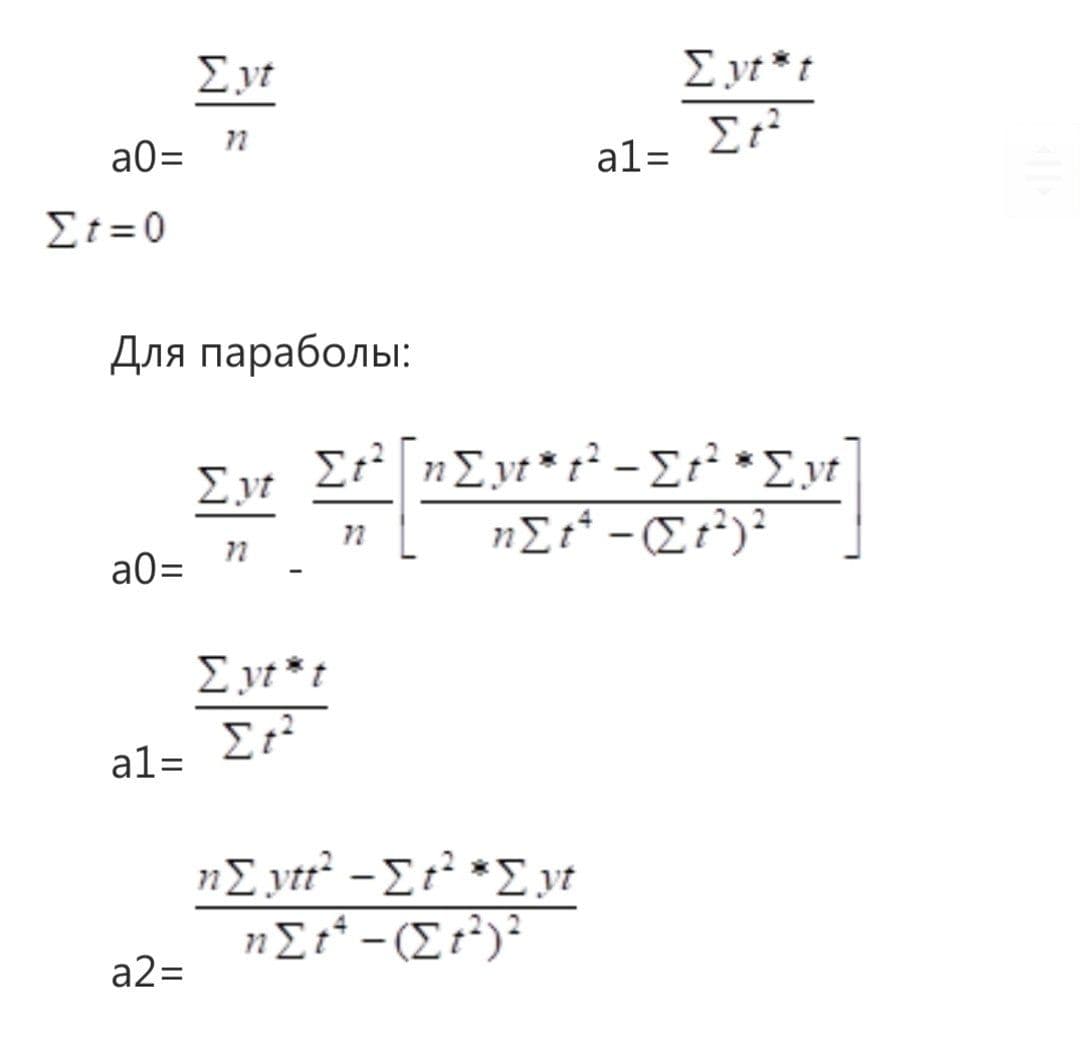 К первому классу кривых роста относятся также экспоненциальные кривые. Для них характерным является зависимость приростов от величины самой функции.. Наиболее часто применяется простая экспоненциальная кривая, которая имеет вид yt=abt Если b>1, то кривая растет вместе с ростом t. Если b<1, то тренд отражает замедляющиеся неравномерно уменьшение уровней. Для нахождения параметров экспоненты данное выражение логарифмируют. Существует другая разновидность экспоненциальных кривых – логарифмическая парабола: Yt= abtct Ко второму классу кривых относят модифицированную экспоненту: yt=к+abt Она описывает процесс, на развитие которого воздействует ограничивающий фактор (асимптота). При решении экономических задач значение асимптоты можно определить исходя из свойств прогнозируемого явления. Иногда значение асимптоты задается экспертным путем. Наиболее часто применяемыми кривыми 3-го класса является кривая Гомперца: yt=к+abt Логистическая кривая:  Пример. Определить параметры параболического тренда  Методы выбора кривых роста Наиболее простой метод – визуальный, опирающийся на графическое изображение временных рядов. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если тенденция на графике просматривается недостаточно четко, то проводят преобразование исходного ряда. В литературе описан также метод последовательных разностей (помогает в выборе кривых параболического типа). Этот метод применяют при выполнении следующих предположений: 1) уровни ряда могут быть представлены в виде суммы трендовой составляющей и случайной компоненты, подчиненной закону нормального распределения с математическим ожиданием, равным нулю и постоянной дисперсией; метод последующих разностей предполагает вычисление первых, вторых и т.д. разностей уровней ряда: Расчет ведется до тех пор, пока разности не будут примерно равными. Порядок разностей принимается за степень выравнивающего полинома. Этот прием можно использовать для преобразования временного ряда. При равных или равных первых разностях можно рассчитать теоретические значения уровней ряда: Утеор =у+ В отдельных случаях используют метод характеристик прироста. Процедура выбора кривых роста с использованием этого метода включает: 1) выравнивание ряда по скользящей средней; 2) определение средних приростов; 3) вычисление производных характеристик прироста Для многих видов кривых были найдены такие преобразования приростов, которые линейно изменялись относительно t или были постоянны. В связи с этим исследование рядов характеристик приростов часто оказывает существенную помощь при определении законов развития исходных временных рядов. Данный метод является более универсальным по сравнению с методом последовательных разностей. Однако, чаще всего на практике к выбору формы кривой подходят исходя из значений критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровня от расчетных, получаемых выравниванием. Из рассматриваемых кривых предпочтение будет отдано той, которой соответствует минимальное значение критерия, т.к. чем меньше значение критерия, тем ближе к кривой ложатся данные наблюдений. Используя этот подход, следует иметь в виду ряд моментов. Во-первых, к ряду, состоящему из m точек можно подобрать многочлен степени (m-1), проходящий через все m точек. Кроме того, существует множество многочленов более высоких степеней, также проходящих через все эти точки. Для этих многочленов значение критерия будет равно 0, однако, очевидно, что такая кривая не слишком пригодна как для выделения тенденции, так и для целей прогнозирования. Также следует учитывать, что за счет роста сложности кривой можно увеличить точность описания тренда в прошлом, однако доверительные интервалы при прогнозировании будут существенно шире, чем у более простых кривых при одинаковом периоде упреждения, например, за счет большего числа параметров. Таким образом, использование этого подхода должно проходить в два этапа. На первом происходит ограничение приемлемых функций, исходя из содержательного анализа задачи. На втором - осуществляется расчет значений критерия и выбор на его основе наиболее подходящей кривой роста. В современных пакетах статистической обработки данных и анализа временных рядов представлен широкий спектр кривых роста. Можно среди этих кривых выбрать отдельную функцию, и получить подробный протокол, включающий оценки параметров, характеристики остатков, прогнозы, интервальные и точечные. Можно выделить на экране несколько функций, тогда протокол будет содержать оценки параметров всех заказанных функций и значения критерия для каждой из них. В качестве критерия выбирается средняя квадратическая ошибка:  Подробный протокол, а также прогнозные значения, на заданное пользователем число временных интервалов, приводятся для функции, отвечающей минимуму указанного критерия. Представляется целесообразным для пользователя на основе выше рассмотренных подходов заранее отвергнуть заведомо непригодные варианты, ограничить поле выбора. В заключение отметим, что нет “жестких” рекомендаций для выбора кривых роста. Особенно осторожно следует подходить к решению этой задачи при использовании полученной функции для экстраполирования найденных закономерностей в будущее. Применение кривых роста должно базироваться на предположении о сохранении выявленной тенденции в прогнозируемом периоде. |
