ответы. Масса м механической системы

• Название: Масса м механической системы
• Дата: 01.04.2022
• Размер: 65.39 Kb.
• Имя файла: ответы.docx
• Тип: Документы; #433610

2. Масса М механической системы равна арифметической сумме масс всех точек или тел, образующих систему: 

масса является мерой инертности тела при поступательном движении.

Центром масс механической системы называют геометрическую точку С, радиус-вектор которой г_с (рис. 16.3) определяется



где r_k — радиус-вектор точек, образующих систему.

Проецируя равенство (16.4) на координатные оси, получаем формулы для координат центра масс системы: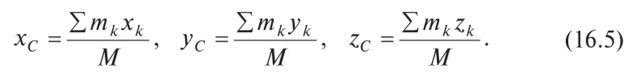



При непрерывном распределении масс суммы, стоящие в правых частях формул (16.4), (16.5), переходят в соответствующие интегралы.

В однородном поле тяжести вес любой частицы тела пропорционален ее массе и центр масс системы совпадает с ее центром тяжести.

В динамике следует говорить о центре масс материальной системы, а не о центре тяжести. При определении центра масс системы можно пользоваться методами, установленными в статике для определения центра тяжести (расчленения, отрицательных масс, симметрии и т. п.).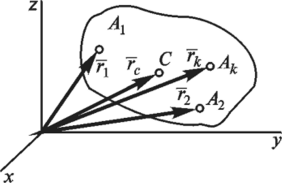



Необходимо отметить, что положение центра масс твердого тела относительно точек этого тела не меняется. Если же система состоит из перемещающихся друг относительно друга материальных точек, то положение центра масс системы относительно ее точек может изменяться.

что центр масс системы является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.

Векторная величина S₀='Em_kr_kназывается статическим моментом масс системы относительно точки О. Скалярная величина S — "Lm^с_А называется статическим моментом масс системы относительно координатной плоскости yz- Величины s_xz — Sm_ky_k и S_x = ^rn_kz_kявляются соответственно статическими моментами масс системы относительно координатных плоскостей и ху.

Радиус-вектор и координаты центра масс системы через статические моменты масс можно выразить формулами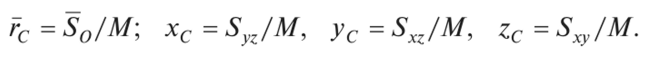



Если в качестве точки О (начала координатных осей) выбрать центр масс С, то S₀= М ? ОС = 0, так как ОС = 0. Следовательно, центром масс системы является точка С, относительно которой статический момент масс системы равен нулю (5_С =0).

1. 
   Ускорение точки в неинерциальной системе отсчета можно в соответствии с (2) представить в виде:
   

Подставим выражение (3) в уравнение (1) и получим:



Это и есть уравнение движения материальной точки относительно неинерциальной системы отсчета. Если в неинерциальной системе отсчета определять силу как вектор, равный произведению массы материальной точки на ее ускорение в этой системе отсчета, то правая часть уравнения (6.4) и является силой, действующей на материальную точку, движущуюся ускоренно в неинерциальной системе отсчета. Эта сила слагается из двух существенно различных составляющих. Первая оставляющая   является результатом взаимодействия тел и проявляется в инерциальной системе отсчета.

Совсем иной характер имеет составляющая –  . Она возникает не из-за взаимодействия тел, а из-за ускоренного движения системы отсчета. Она называется поступательной силой инерции. При переходе к другой ускоренно движущейся системе отсчета меняются и силы инерции. Эти силы инерции отличаются от настоящих сил, возникающих при взаимодействии тел. Второе отличие состоит в том, что силы инерции не подчиняются закону действия и противодействия (третьему закону Ньютона).

При описании движения тел относительно ускоренно движущейся поступательно системы отсчета наряду с силами, обусловленными взаимодействием тел друг с другом, необходимо учитывать так называемые силы инерции  . Эти силы следует полагать равными произведению массы тела на взятое с обратным знаком ускорение движущейся неинерциальной системы отсчета относительно инерциальной системы:



Соответственно, уравнение движения в неинерциальной системе отсчета будет иметь вид



Существует много явлений, которые могут быть интерпретированы как проявление силы инерции. Когда поезд набирает скорость, пассажиры в вагоне испытывают действие силы, направленной против движения поезда. Это и есть сила инерции. Силы инерции вызывают перегрузки, действующие на летчика при больших ускорениях самолета. Если в ускоренно движущемся вагоне висит шарик массы m, то сила инерции отклоняет его в сторону, противоположную ускорению (рис.1).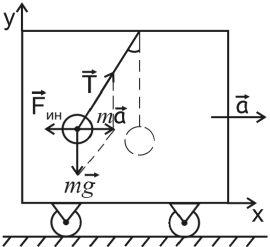



Рис.1

 

Нить отклоняется на такой угол, чтобы результирующая двух сил ( ) сообщала шарику ускорение  , с которым движется вагон. Относительно системы отсчета, связанной с вагоном, шарик покоится. Это можно объяснить, если ввести силу инерции  , уравновешивающую результирующую двух сил   и  .

Введение сил инерции дает возможность описывать движение тел в любых системах отсчета с помощью одних и тех же уравнений движения.

Силы инерции имеют характерные особенности: они не отражают взаимодействие тел, а обусловлены характером неинерциальных систем отсчета, поэтому для сил инерции неприменим третий закон Ньютона. Характерным свойством сил инерции является их пропорциональность массе тела. Благодаря этому свойству силы инерции оказываются аналогичными силам тяготения. Движение тел под действием сил инерции сходно с движением в гравитационном поле. В качестве примера можно привести невесомость, возникающую в свободно падающем лифте. В свободно падающем лифте вес   тела массой m всегда равен нулю:  .

Действительно:





Рассмотрим силы инерции, возникающие во вращающихся системах отсчета.

1.