Комова моя математическая грамотость. Математическая грамотность Комова Инна Петровна

• Название: Математическая грамотность Комова Инна Петровна
• Дата: 18.02.2023
• Размер: 0.8 Mb.
• Имя файла: Комова моя математическая грамотость.doc
• Тип: Документы; #942951

Математическая грамотность

Комова Инна Петровна,

учитель математики МБОУ СОШ №1
Эта разработка является итогом обучения на курсах «Цифровая экосистема». В ходе занятий необходимо было выполнить практические задания по разным темам. Ситуация была предложена разработчиками курсов, а задания к ситуации нужно было составить обучающимся. В этой статье приводятся задания, разработанные мной в ходе обучения.

1. 
   Основные понятия
   

Математическая грамотность—это способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира.

Контексты — это особенности и элементы окружающей обстановки, представленные в задании в рамках описанной ситуации

(личный, общественный, профессиональный и научный).

Математическое содержание разделяется на блоки:

-изменение и зависимости – задания, связанные с математическим описанием зависимости между переменными в различных процессах, т.е. с алгебраическим материалом;

-пространство и форма – задания, относящиеся к пространственным и плоским геометрическим формам и отношениям, т.е. к геометрическому материалу;

-количество – задания, связанные с числами и отношениями между ними, в программах по математике этот материал чаще всего относится к курсу арифметики;

-неопределённость и данные – задания охватывают вероятностные и статистические явления и зависимости, которые являются предметом изучения разделов статистики и вероятности.
Задания по направлениям
1. Распознавание математических понятий, объектов и закономерностей в реальных жизненных ситуациях

1. 
   Задача про гаджеты.
   

Трудно представить жизнь современного школьника без гаджетов, которые они используют для общения, обучения и развлечений. Однако, по мнению специалистов, гаджеты приносят школьникам не только пользу, но и вред здоровью – ухудшают зрение, портят осанку, влияют на нервную систему и др. Поэтому специалисты рекомендуют детям до 12 лет проводить за компьютером не более 1,5 часа в день.

Егору 11 лет, он учится в шестом классе и как все его сверстники очень любит гаджеты. Мама Егора решила посчитать, сколько времени он проводит с гаджетами. Один день она записывала все время, проведенное Егора с гаджетами, а затем занесла полученные данные в таблицу.

Использование гаджета	Количество времени
Общение с друзьями в социальных сетях	15.00-16.00, 21.00-21.30
Подготовка к зачетной работе по математике с помощью ресурсов Интернет	17.00-17-30
Игры на телефоне	19.00-20.00
Просмотр видеороликов на различных ресурсах Интернет	20.00-21.00

Задание 1.1 Соответствует ли время, которое проводит Егор с гаджетами, рекомендациям специалистов? Ответ: не соответствует

Задание 1.2 Специалисты советуют целесообразно перераспределить время использования гаджетов:

-на помощь в обучении - 25% времени;

-на общение с друзьями — 20% времени;

-на развитие навыков работы с программами-приложениями — 2/5 времени;

-на развлечения- остальное время.
Сколько времени в минутах максимально может составить просмотр Егором видеороликов на сервисе ТикТок согласно этому распределению?

Выберите один из ответов:

1. 
   15 мин;
   
2. 
   13,5 мин;
   
3. 
   10,5 мин;
   
4. 
   60 мин.
   

Решение: 2\5 это 40%, значит на полезные дела уходит 25%+20%+40%=85%

на развлечения 15%, т. е. 90 мин х 0,15=13,5 мин. Верный ответ 2)

Задание 1.3 В 12 лет время использования гаджетов по рекомендациям специалистов может увеличиться на 2/3. Сколько минут в день сможет просматривать Егор видеоролики на сервисе ТикТок после исполнения 12 лет?

Решение: 2\3 от 90 мин это 60 минут, значит общее время составит 150 минут.

150 х 0,15 =22,5 минуты.

Задание выполнено верно, если приведены все рассуждения и дан верный ответ.



Задание 2. Проблемы загрязнения окружающей среды
20 декабря 2013 года Генеральная Ассамблея ООН провозгласила 3 марта Всемирным днем дикой природы с целью повысить уровень осведомленности широкой общественности в вопросах дикой фауны и флоры. В школе ежегодно проводятся акции в защиту животных. Учащиеся принимают участие в конкурсах плакатов и проектов, посвященных сохранению природной среды.

В школе всего учится 540 учащихся, из них – 35% учащихся начальной школы, 30% учащихся 5-6 классов и 25% учащихся 7-9 классов, остальные – учащиеся 10-11 классов.

Задание 2.1 Учащиеся старших классов вышли на уборку берега реки от различного бытового мусора. Каждый ученик 10-11 классов собрал до 10 кг мусора. Сколько контейнеров потребуется для вывоза собранного мусора, если в каждый контейнер входит до 100 кг?

Решение: 35%+30%+25%=85%, значит ученики 10-11 классов составляют 10%. 540 х 0,1= 54 ученика. 54 х 10= 540 (кг) мусора всего убрано. 540:100=5(40 остаток). Значит потребуется 6 контейнеров.
Задание выполнено верно, если приведены все рассуждения и дан верный ответ

Задание 2.2 Пятиклассники провели опрос в своей школе и выяснили, что ребята считают основными причинами, по которым животные лишаются еды и крова:

• 
  осушение болот — 45 % опрошенных;
  
• 
  вырубку лесов — 50% опрошенных;
  
• 
  охоту браконьеров -10 человек.
  

Можно ли утверждать, что более 210 человек из опрошенных считают основными причинами голода в животом мире экологические проблемы?Решение: 45%+50%=95%, значит 10 человек это 5%. Значит всего опрошено 10 х 20=200 человек. 210>200, и больше 190, значит это невозможно.

Задание выполнено верно, если приведены все рассуждения, обоснован выбор экологических проблем и дан верный ответ


Задание 3
На рисунке изображено 5 фигур, составленных из четырех окружностей.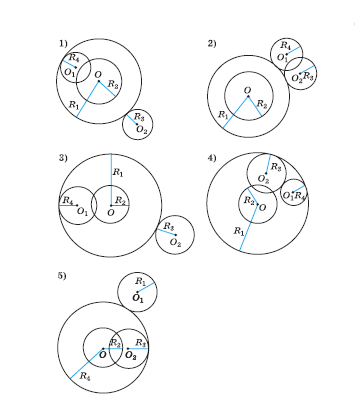


Выберите фигуру, которая удовлетворяет каждому из приведенных условий:

а) Две окружности касаются третьей ;

б) Расстояние от центра окружности О до центров окружностей О1 и О2 больше радиуса R1;

в) ОО1=ОО2;

г) окружности О1 и О2 пересекаются в двух точках;

д) Треугольник с вершинами О, О1 и О2 равнобедренный.

2. Построение математических моделей и обоснованный выбор математического аппарата для решения реальных проблем

З адание 1. Клумба

Для создания клумбы площадью 10 кв.м в городском парке необходимы луковицы тюльпанов и нарциссов. Плотность посадки луковичных растений на 1 кв.м следующая: тюльпаны – 15-18 шт., нарциссы – 12-15 шт.

Озеленители решили разбить клумбу, ⁴ 4/5 площади которой занимают нарциссы, а остальную часть – тюльпаны.

1.1 Пусть площадь, занятая тюльпанами — х кв.м, а нарциссами у кв. м. Общее количество растений, удовлетворяющее условиям задания, обозначим Р. Какое наименьшее количество Р растений понадобится для озеленения клумбы?

Выберите математическую модель для решения задачи.

а) Р = 15х+12у;

б) Р = 18х+15у;

в) Р = 15х+15у;

г) Р = 18х+15у.

1.2 Дайте ответ на вопрос: какое минимальное количество растений понадобится для посадки? ________________

1.3 Изменится ли математическая модель решения задачи, если площадь, занятая тюльпанами, будет составлять 3\10 площади клумбы?

1. 
   да;
   
2. 
   нет.
   

1.4 Дайте ответ на вопрос: какое минимальное количество растений понадобится при таком распределении площади, отведенной под нарциссы и тюльпаны?

Оценивание: верный выбор варианта ответа в заданиях 1.1 и 1.3 и верный ответ на вопрос 1.2 и 1.4.

Решение: х=10*(1/5); у=10*(4/5)

вариант а) Р=15*2+12*8=126 растений всего.

В вопросе 1.3 верный ответ 2). Формула не изменится, изменятся значения х=3 и у=7. В задании 1.4 Р=3*15+7*12=129

З адание 2. Помощь

Учащиеся школы узнали, что брату одного из учеников требуется дорогостоящая операция, и решили оказать посильную помощь в сборе средств. На Ученическом совете было принято решение собрать макулатуру и провести благотворительную ярмарку и вырученные деньги отдать в фонд помощи больному ребенку. В сборе макулатуры принимали участие ученики начальной, основной и старшей школы. Учащиеся начальной школы собрали 20% всего объема собранной макулатуры, учащиеся основной школы – 50% , остальную макулатуру собрали учащиеся старшей школы. Килограмм макулатуры можно сдать в приемный пункт по цене 18 рублей за 1 кг.

1. 
   Какая диаграмма точнее соответствует распределению собранной макулатуры по ступеням обучения? Выберите один из вариантов ответа.
   

а)

б)






в)

2. 
   Операция стоит 5000 рублей. Каким может быть минимальное значение А (целое количество собранной макулатуры, в кг) в формуле, дающей общую сумму, собранную школьниками, чтобы денег на оплату операции хватило:
   

а) А х 18 >= 5000;

б) А х 18 < =5000.

Выберите вариант, который считаете верным и запишите ответ в поле ___________.

Как изменится математическая модель, если нужно определить сумму денег, собранных учащимися старшей школы, при условии, что набрана нужная сумма.

Запишите в ответе математическую модель __________________. Вычислите эту сумму в рублях.______________

Решение: В задании 2.1 верно показано распределение на диаграмме б).

В задании 2.2 верная формула а). А= 5000/18 ≈ 278 кг. Старшая школа должна собрать 278*0,3≈84 кг. В рублях 84 кг*18=1512 р.

3. 
   
   

З адание 3. Марафон

Понятие марафонский бег появилось в 490 году до нашей эры, когда состоялась битва у древнегреческого города Марафон, после чего воин Фидиппид помчался в Афины, чтобы объявить о долгожданной победе. Он был так измучен бегом на длительную дистанцию, что умер сразу же после выполнения своей миссии. В 1896 году в мире состоялись первые Олимпийские игры, в которые был включен и марафон. С 1970 года непрофессиональные марафоны приобрели в США огромную популярность, в них стали активно принимать участие даже старики. Сегодня марафоны проводятся по всему миру и в них участвуют люди разных возрастных категорий.

Московский марафон — крупнейшее соревнование по бегу в г. Москве, проводимое ежегодно с 2013 года в конце сентября. В таблице представлены данные количества участников Московского марафона с 2013 по 2019 гг.

Дата	Дистанция	Финишировало
22.09.2019	42,195 км	10452
	10 км	12701
23.09.2018	42,195 км	8761
	10 км	12696
24.09.2017	42,195 км	7680
	10 км	12972
25.09.2016	42,195 км	7813
	10 км	10944
20.09.2015	42,195 км	5566
	10 км	8105
21.09.2014	42,195 км	4031
	10 км	5267
15.09.2013	42,195 км	2366
	10 км	2412

1. 
   Проанализируйте изменение количества участников забега на дистанции 10 км. В каком году году был самый большой прирост числа участников и на сколько процентов?
   

Ответ: год ___________; прирост в процентах ____________

2. 
   Марафон на дистанции 42,195 км тяжелое испытание для организма спортсмена и не все стартовавшие доходят до финишной черты. Часть участников сходит с дистанции, (примерно 15%). Определите возможное число стартовавших участников в 2019 году?
   

Ответ округлить до целого. __________
Решение: для наглядности нужно составить новую таблицу участников марафона на 10 км и найти прирост числа участников за каждый год и вычислить в процентах от предыдущего года. Далее выбрать самый большой прирост и выразить а сколько в процентах. В задаче 3.2 10452 участника составляют 85% от стартовавших. 10452/0,85≈ 12296 человек
3. Развитие оценки и аргументации выводов

на основе математических знаний
Завершающим этапом математического моделирования, обеспечивающим адекватное использование его результатов, является этап интерпретации и оценки. Результатом этого этапа является получение оценочных суждений и их аргументация. Умение высказывать собственные оценочные суждения и их корректно аргументировать лежат в основе формирования таких навыков, как критическое мышление, саморегуляция деятельности, рефлексия и коммуникация. От наличия этих умений зависит становление личности, способной к самостоятельному принятию ответственных решений.

Задача1. Пирамида населения

Познакомьтесь с возможностями ресурса «Возрастно-половая пирамида населения».

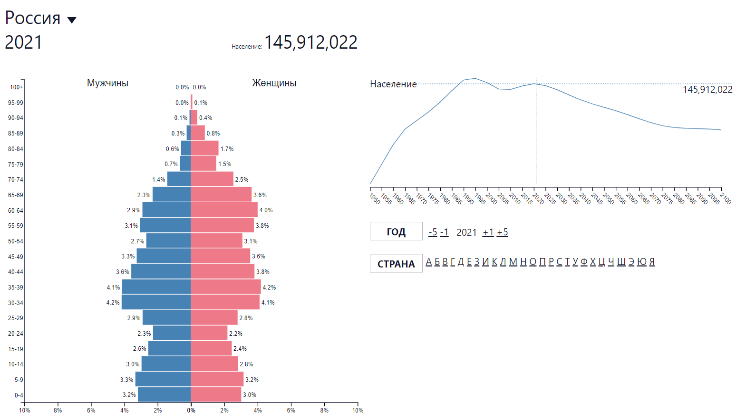
Используйте знания математики и ее возможности, чтобы оценить утверждения в представленных ниже категориях. Для ответа поставьте знак «+» в соответствующей ячейке таблицы.

Утверждения	Истина	Ложь	Невозможно установить
1. По результатам переписи 2021 года в России нет ни одного жителя, относящегося к категории 100 +.		+
2. Количество мужчин и женщин становится примерно одинаковым в возрасте около 30-40 лет. Можно установить возраст установления равновесия числа мужчин и женщин с точностью до одного года			+
3.Численность населения в возрасте 19-23 лет в 2021 году существенно меньше, чем в других трудоспособных возрастах	+
4.По международным критериям население считается старым, если доля людей в возраст старше 65 лет составляет больше 7% населения страны. Население России в 2021 году не является старым		+

Задача 2. «Решение о покупке» недостающими данными: вид товара, замечание о связи множества отзывов и множества оценок, отзывы покупателей, утверждения.

Примечание: Утверждения формулируйте так, чтобы поставленные в таблице оценки были верны.

Решение о покупке

Иван решил приобрести ___телефон марки Айфон 12-PRO__(корпус красного цвета)_______через интернет-магазин. Он оценивает риски покупки товара, ориентируясь на отзывы покупателей (проценты отображаются на диаграмме с точностью до целых).



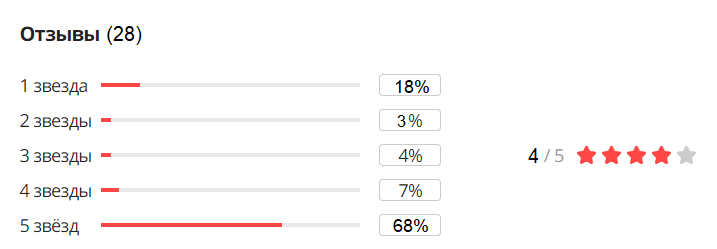
Иван проанализировал все отзывы покупателей интернет-магазина, заметил__каждая претензия содержала только одну позицию_ и составил таблицу высказываний покупателей.

Высказывания	Кол-во
Товар доставили позже указанного срока	5
Телефон оказался модели Айфон12, т. е. не соответствовал заказу	3
Телефон оказался подделкой	2
Доставленный телефон оказался другого цвета	7

Используйте эти данные, чтобы определить, какие из следующих ниже утверждений являются истинными всегда, иногда или никогда. Поставьте в каждой строке только одну метку (в таблице представлено возможное заполнение).

Утверждение	Всегда	Иногда	Никогда	Невозможно установить
1. По крайней мере 19 покупателей интернет-магазина поставили 5 звезд наушникам	+
2. Рейтинг телефонов может повыситься до 5				+
3.Претензия покупателя связана с проблемой доставки		+
4.Претензии связаны с неисправностью телефона			+
5.Все претензии связаны с нарушением содержания заказа	+
6.Интернет-магазин отказался от заказа			+

При выполнении таких заданий учащимся потребуется продемонстрировать, как они умеют размышлять над аргументами, обоснованиями и выводами, над различными способами представления ситуации на языке математики, над рациональностью применяемого математического аппарата, над возможностями оценки и интерпретации полученных результатов с учетом особенностей предлагаемой ситуации. Составление таких заданий требует от учителя большой эрудиции, поскольку задания не должны повторять стандартные математические формулировки.