математическая круговерть. Математическая круговерть
 Скачать 23.77 Kb. Скачать 23.77 Kb.
|
|
Математическая круговерть. Горлатова М. В., учитель математики МБОУ «СОШ с. Натальин Яр Перелюбского муниципального района Саратовской области» Перед изучением круга и окружности предложите ребятам загадки. Они наверняка их отгадают. Мой циркач, циркач лихой, Чертит круг одной ногой, А другой проткнул бумагу, Уцепился и ни шагу. (Циркуль) А для чего нужен циркуль? (Чтобы чертить круги и окружности). У круга есть одна подруга, Знакома всем её наружность, Она идёт по краю круга И называется … (окружность). С кругом и окружностью на уроках приходится встречаться довольно часто. И при каждой встрече хорошо бы узнавать о них что-то новое, неизвестное, интересное. Все умеют с помощью циркуля начертить окружность и круг. А все ли знают, что означает слово «циркуль»? Не пожалейте времени и доведите до сведения учеников (или попросите их найти значение этого слова в словаре), но пусть школьники узнают, что «циркуль» и «цирк» - это слова родственники. Ведь оба слова происходят от латинского «циркус», что означает «круг». Многие ли дети были в цирке? Устройте им хотя бы виртуальное путешествие в цирк. А потом можно и задачу предложить. Задача. Цирковая арена имеет форму круга. Её диаметр равен 13,5 м. Какова её площадь?( Решение. S 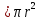 ; S=3,14·13,52=3,14·182,25 =572,265 м2). Ну уж если мы попали в цирк, то как пройти мимо затейливых фокусов и трюков? ; S=3,14·13,52=3,14·182,25 =572,265 м2). Ну уж если мы попали в цирк, то как пройти мимо затейливых фокусов и трюков?Цифра девять иль девятка - цифровая акробатка, Если на голову встанет, цифрой шесть девятка станет. Загадка. Что не поместится даже в самой большой кастрюле? (Крышка от этой кастрюли) Проблемный вопрос. Почему крышки уличных люков делают не квадратными, а круглыми? (Если квадратную крышку люка поставить на ребро, то она может проскользнуть в люк и упасть на рабочего. Этого не произойдёт с круглой крышкой). В формулах площади круга и длины окружности есть число 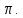 Означает оно отношение длины окружности к длине её диаметра. И ученики быстро запоминают его числовое значение 3,14. И этому числу уделите немного внимания. И ради интереса можно запомнить и большее количество десятичных знаков этого числа. Для этого есть мнемонические правила, где количество букв в слове равно цифре числа Означает оно отношение длины окружности к длине её диаметра. И ученики быстро запоминают его числовое значение 3,14. И этому числу уделите немного внимания. И ради интереса можно запомнить и большее количество десятичных знаков этого числа. Для этого есть мнемонические правила, где количество букв в слове равно цифре числа 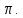 Это я знаю и помню прекрасно, Пи – лишние знаки тут чужды, напрасны (3, 14159265358). Тут и Миша и Анюта прибежали пи узнать число они желали (3, 1415926536). А можно, например, в виде стихотворения. Нужно только постараться И запомнить всё как есть: 3, 14, 15, 92 и 6. Задача (практико-ориентированная) Отец Вали и Веры предложил девочкам сделать две клумбы. Он дал им верёвку длиной 6 м, чтобы с её помощью наметить границу каждой клумбы. Валя решила сделать клумбу квадратной, а Вера – круглой. Чья клумба будет иметь большую площадь? Радиус круглой клумбы вычислите с точностью до сотых. Во сколько раз площадь одной клумбы больше площади другой? Решение. Для квадратной клумбы длина 6м является периметром, тогда длина стороны квадрата равна 6:4 = 1, 5(м), а площадь квадрата S = 1,5·1,5 = 2, 25(м2). Для круглой клумбы длина верёвки является длиной окружности. C = 2 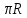 . 6=2·3,14R, откуда . 6=2·3,14R, откуда R =6:6,28 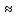 0,96(м). Площадь круглой клумбы 0,96(м). Площадь круглой клумбы S= 3, 14·0,962 =3,14·0,9216 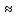 2,9(м2). 2,9(м2).Площадь круглой клумбы оказывается в 2,9:2,25 = 1,2 раза больше площади квадратной клумбы. Решая эту задачу (а ещё лучше, если выполнить практическую работу непосредственно на земле), ребята получают практический опыт или знания, которые могут им пригодиться в реальной жизни. Немного истории. Столько купили земли и дали ей имя Бирса, Сколько могли окружить бычьей шкурой. Вергилий «Энеада» В жизни постоянно приходится сталкиваться с необходимостью принять наилучшее возможное (оптимальное) решение. Огромное число таких задач возникает в экономике и технике. В математике исследование задач на максимум и минимум началось очень давно – 25 веков назад. Примерно 300 лет назад – в эпоху формирования математического анализа – были созданы общие методы решения задач на экстремум. Приведенные в эпиграфе строки относятся к событию, произошедшему, если верить преданию, в IXвеке до нашей эры. Финикийская царевна Дидона, спасаясь от преследований своего брата, отправилась на запад вдоль берегов Средиземного моря искать себе прибежище. Ей приглянулось одно место на берегу нынешнего Тунисского залива. Дидона повела переговоры с местным предводителем Ярбом о продаже земли. Запросила она совсем немного – столько, сколько можно «окружить бычьей шкурой». Дидоне удалось уговорить Ярба. Сделка состоялась, и тогда Дидона изрезала бычью шкуру на мелкие тесемки, связала их воедино и окружила большую территорию, на которой основала крепость, а вблизи от нее – город Карфаген. Во время изучения темы «Окружность и круг» можно предложить ребятам сочинить самим или найти в интернете и выучить стихи об этих фигурах. Любят Круг все поголовно, всяк признать его готов За его характер ровный – не имеет он углов. Круг есть всюду - каждый знает. Парадокс, но это так: В жизни круглыми бывают и отличник, и дурак. В нашей сложной круговерти, оглянитесь-ка вокруг, Вот уж несколько столетий крутится гончарный круг. А возьмите круг вопросов, тех, кто с техникой знаком, Только круглые колеса нас прокатят с ветерком. Формы у плодов природных в большинстве своем круглы, И для встреч международных ставят круглые столы. Наша круглая планета, совершая свой полет, Кружит и зимой и летом вокруг Солнца круглый год. Честно служит Круг всем людям, без него нам не прожить. Не напрасно Круг мы любим, есть за что его любить! Н. К. Шабалина Хорошо, когда ребята могут приводить примеры предметов быта и предметов из окружающей обстановки, имеющих форму круга, форму окружности. Покажите им, как эти фигуры изображаются на плоскости. Предложите нарисовать предметы, где ребятам пригодится это умение: стакан, ваза, чайная чашка и т.п. Считаю, что и творческие задания удачно впишутся в урок или во внеклассное занятие. Можно предложить ребятам придумать и изобразить с помощью циркуля узоры или рисунки (цветы, орнамент, снеговик, медвежонок и т. п.) А можно и поиграть в слова. Кто больше составит за одну минуту слов из букв, с помощью которых записано слово ОКРУЖНОСТЬ. И, конечно же, очень важен набор задач, которые будут предложены для решения дома, на занятиях кружка, в качестве индивидуальных заданий. Причём подготовить подборку задач вам могут помочь сами обучающиеся. Задача. Хозяйка, приведя козу на пастбище, вбила 2 колышка А и В на расстоянии 4 м друг от друга и натянула между ними верёвку с кольцом, которое свободно перемещалось по ней. К кольцу привязала верёвку с козой. Нарисуйте образовавшееся пастбище, если длина верёвки 2 м. Вычислите площадь образовавшегося пастбища и длину ограничивающей его линии. Решение. Образовавшееся пастбище будет представлять из себя квадрат со стороной 4м , с двух противоположных сторон которого добавлены два полукруга радиусом 2 м. Тогда площадь будет равна сумме их площадей, т.е. 42 + 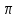 ·22 = 16 +4 ·22 = 16 +4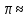 16+4·3, 14 16+4·3, 14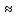 28,56(м2) 28,56(м2)Набор задач прикладного характера. Зрачок человеческого глаза в зависимости от степени яркости света изменяется в размере от 2 мм до 6 мм. Во сколько раз площадь расширенного зрачка больше площади суженного? Сколько материи потребуется, чтобы сшить юбку-солнце (обрезки будут использованы для другого изделия)? R1= 100 см, R2 = 10 см? Вагонное колесо имеет диаметр 1,15м. Сколько оборотов оно делает на протяжении 1 км? На сколько удлинился бы экватор глобуса, если бы его радиус был на 1 см больше? На сколько удлинился бы при таком же увеличении радиуса земной экватор? Если бы мы могли обойти земной шар по экватору, то макушка бы нашей головы описала бы более длинный путь, чем каждая точка ступней. Как велика эта разница, если рост человека равен 1,75 м? Сколько пленки потребуется, чтобы накрыть сверху бассейн радиусом 3 м? Рассчитайте количество плиток со стороной 10 см, необходимых для огораживания круглой клумбы радиусом 3 м. Рассчитайте длину металлической полоски, чтобы обить колесо для телеги радиусом 30 см. Решая задачи про колёса, можно предложить ученикам найти материал об изобретении колеса. А можно поработать с такими устойчивыми словосочетаниями как «белка в колесе», «круговая порука», «круглый отличник» или «круглая дата», выяснить, откуда пошли такие выражения. Эту благодатную тему можно изучать всесторонне. Главное, привлечь внимание учеников. И, конечно же, не надо преподносить им готовые знания и факты, а нужно мотивировать ребят на самостоятельные открытия. Список использованных источников: Гарднер М., «Крестики – нолики». –М., «Мир», 1988 г. Киселёв А. П. Элементарная геометрия. Кн. для учителя. М., «Просвещение», АО «Учебная литература», 1996. Смирнова Е. С. Курс наглядной геометрии. М., «Просвещение», 2002 г. Шеврин Л. Н., Гейн А. Г., Коряков И. О., Волков М. В. Математика 5-6. Учебник-собеседник. М., «Просвещение», 1989 г. http://школапифагора.рф/blog/stikhotvorenija_k_urokam_matematiki_na_temu_quot_okruzhnost_i_krug_quot/2013-07-30-40 http://festival.1september.ru/articles/585531/ |
