МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Ульяновский государственный университет»
Факультет математики, информационных и авиационных технологий
Кафедра прикладной математики
КУРСОВАЯ РАБОТА
на тему «Математическая модель Броуновского моста »
(Тема курсовой работы)
Выполнила:
Студентка группы___ПМ-О-19/1_____
Багаутдинова А.Н./_______________
(Фамилия И.О. / подпись)
«_____» _________________20_____г.
Научный руководитель:
Помощник ректора, Профессор,
Заведующий кафедрой
доктор физико-математических наук
(Степень, должность)
Бутов А.А/_______________
(Фамилия И.О. / подпись)
Оценка ______________________________
«_____» _________________20_____г.
Ульяновск, 2021 г.
Содержание:
Стр.
Введение ………………………………………………………...………….………3
1.Основные понятия и определения из теории вероятности …………………..5
2.Связь с другими случайными процессами ………………………………….9
2.1 Свойства связи с другими случайными процессами …………………….9
2.2 Вспомогательные связи и определении….….….….….…..….….…..…. 12
Заключение…… …………….……………….………………….……….....…..13
Список использованной литературы…………………..……...…..………….14
ВВЕДЕНИЕ
Математическая модель броуновского движения была впервые построена Н.Винером. Броуновское движение рассматривается как винеровский процесс – непрерывный случайный процесс с независимыми приращениями, которые подчиняются нормальному (Гауссову) распределению с математическим ожиданием, равным нулю. Дисперсия в этом распределении имеет значение, полученное в теории Эйнштейна. Это означает, что на каждом выбранном временном интервале частица совершает перемещение, значение которого не зависит от движения в более ранние моменты времени. Временные интервалы не перекрываются. Среднее значение всех перемещений за достаточно долгий промежуток времени равно нулю. А среднее значение квадрата отклонения в соответствии с формулой Эйнштейна равно : < S2 > = 6Dt
Дан случайный процесс “Броуновский мост” на интервале [0,1]. Броуновский мост— это частный случай случайного блуждания с непрерывным временем (винеровского процесса)B(t) , когда начальная и конечная точки совпадают: B(0)= B(1) = 0 .
Стандартный винеровский процесс "привязан" в начальной точке W(0) = 0 , но имеет свободный конец. Броуновский мост зафиксирован и в начале B(0) = 0 , и в конце B(1) = 0 .
Броуновский мост имеет среднее E[Bt] = 0 и дисперсию D[Bt] = t(1 - t) , что подразумевает наибольшую неопределенность в середине моста и полную определенность на концах. Ковариация COV[ Bs , Bt ] = s(1 - t ) , где s < t. Приращения не являются независимыми.
В общем случае B( t1 ) = a и B( t2 ) = b . Тогда
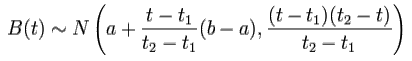
При t ∈( t1, t2 ) .
В нашем случае B( t ) N( 0, t( l - t )
ГЛАВА 1. Основные понятия и определения
Отметим, что в книге Седжвика, Уэйна и Дондеро под броуновским мостом понимается некоторая кривая. В общепринятом же смысле, броуновский мост — это случайный процесс, удовлетворяющий некоторым требованиям. А упомянутая кривая — это лишь график одной из реализаций этого процесса.
Но нас сейчас не будут интересовать случайные процессы. Мы собираемся лишь рисовать кривые и поэтому примем то определение броуновского моста, которое можно сконструировать, руководствуясь книгой "Программирование на языке Python: учебный курс".
Итак, будем считать, что броуновский мост — это кривая, которая строится по следующему принципу.
Рассмотрим на координатной плоскости две точки с координатами (x1; y1) и (x2; y2), где x1 < x2.
На первом шаге построим точку (x3; y3), где
x3 = (x1 + x2) / 2,
y3 = (y1 + y2) / 2 + δ1.
Таким образом, построенная точка — это середина отрезка, соединяющего точки (x1; y1) и (x2; y2), смещённая вверх или вниз (в зависимости от знака δ1) по оси ординат.
На втором шаге по тому же принципу строим точки (x4; y4) и (x5; y5), где
x4 = (x1 + x3) / 2,
y4 = (y1 + y3) / 2 + δ2,
x5 = (x3 + x2) / 2,
y5 = (y3 + y2) / 2 + δ2.
Точно таким же образом действуем и на последующих шагах. На каждом i-м шаге строим 2i точек, абсциссы которых есть средние арифметические абсцисс двух соседних, уже построенных до этого шага точек, а ординаты отличаются от средних арифметических ординат соседних точек на δi. В результате n шагов таким образом оказываются построенными 2n − 1 точек (назовём их "внутренними").
Поговорим теперь более подробно о числах δi. Эти числа выбираются случайным образом. Каждое такое число представляет собой значение случайной величины, распределённой по нормальному закону, с математическим ожиданием, равным 0, и среднеквадратическим отклонением, равным σ / αi − 1.
Здесь σ — это начальное среднеквадратическое отклонение, применяющееся на первом шаге. А на каждом последующем шаге среднеквадратическое отклонение, как мы видим, получается из предыдущего делением на α. Так что среднеквадратичное отклонение на i-м шаге можно рассматривать как начальное отклонение, умноженное на "масштабирующий коэффициент", равный α1 − i.
Параметр α находится по формуле α = 2H. Здесь H — это так называемый показатель Херста.
Нужно иметь в виду, что для каждого фиксированного i все числа δi (в количестве 2i) — вообще говоря, разные. Я не использовал второй индекс в обозначениях этих чисел лишь для упрощения обозначений.
Итак, в результате выполнения n шагов мы имеем 2 исходные точки и 2n − 1 внутренних точек. Упорядочиваем эти 2n + 1 точек в порядке возрастания их абсцисс, после чего соединяем их последовательно отрезками, двигаясь от первой к последней. В результате получаем ломаную, состоящую из 2n звеньев и 2n + 1 вершин. Эта кривая и есть броуновский мост.
Если начало и конец ломаной фиксированы, то форма её определяется двумя параметрами: σ и H (разумеется, определяется не полностью, поскольку на неё также влияют случайные факторы).
От первого из них зависит, насколько сильно в среднем будет отклоняться каждая вершина ломаной от отрезка, соединяющего две соседние по отношению к ней вершины. Можно сказать, что σ влияет на "амплитуды колебаний".
Второй параметр влияет на "плавность" кривой. Чем больше H, тем более плавной выглядит кривая.
Ясно, что броуновский мост состоит из двух броуновских мостов, конец первого из которых совпадает с началом второго. В свою очередь, каждый из этих двух мостов также состоит из двух мостов и т. д. Таким образом, явно прослеживается рекурсивная природа нашей кривой. Становится понятным, что наиболее простой способ построения такой кривой — использование рекурсивной функции. Именно такую функцию мы и построим.
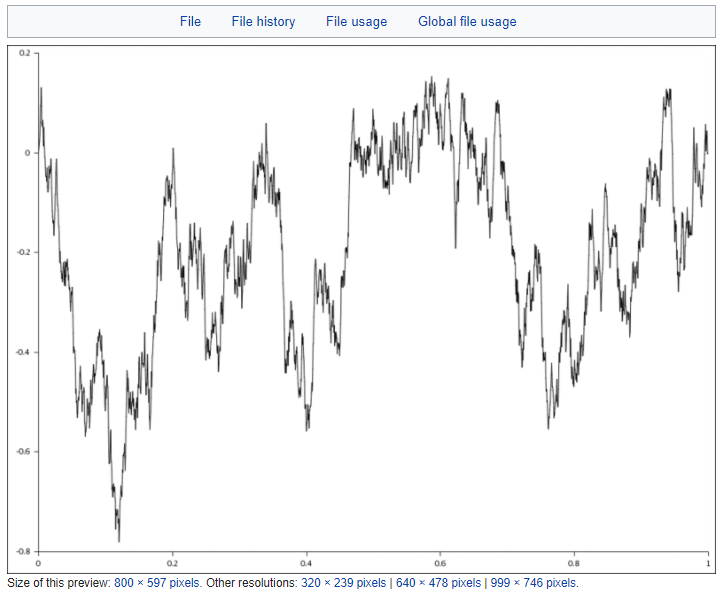
Рис. 1.Броуновское движение, закрепленное с обоих концов. Здесь используется броуновский мост.
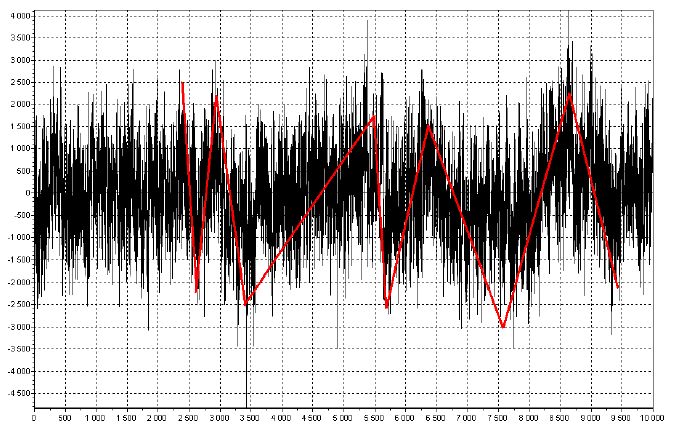
Рис. 1. Броуновский мост (показатель Херста 0,9).
ГЛАВА 2.Связь с другими случайными процессами
2.1 Свойства связи с другими процессами
Если W(t) — стандартный винеровский процесс (т.е. для t ≥ 0, W(t) нормально распределено со средним 0 и дисперсией t, а приращения являются независимыми), то имеем броуновский мост B(t)=W(t)−t⋅W(1)B(t)=W(t)−t⋅W(1) В свою очередь, если взять броуновский мост B(t) и стандартную нормально распределенную случайную величину Z, то процесс W(t)=B(t)+tZW(t)=B(t)+tZ будет винеровский процессом для t ∈ [0, 1]. В общем, при t ∈ [0, T] имеем W(t)=B(tT)+tT√ZW(t)=B(tT)+tTZ Броуновский мост является следствием применительно к эмпирическим процессам . Также он используется в критерии согласия Колмогорова-Смирнова для статистического вывода.
Свойство 1:
Если это винеровский процесс (или броуновское движение), то процесс, определяемый посредством, является стандартным броуновскиммостом.
(Wt,t ≥ 0)(Bt,0 ≤ t ≤ 1)Bt, = Wt - tW1
Взаимный:
Если это стандартный броуновский мост и Z является нормальной случайной величиной , то процессы и определяются по формуле:
( Bt , 0 ≤ t ≤ 1 )( Wt1 , 0 ≤ t ≤ 1)( Wt2 , 2 ≤ t ≤ T)
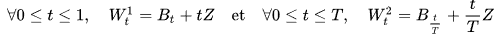
Винеровские процессы.
Свойство 2:
Если это винеровский процесс, то процесс, определенный с помощью, является стандартным броуновским мостом.
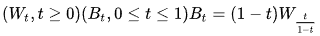
Взаимный:
Если - стандартный броуновский мост, то процесс, определяемый с помощью, является винеровским.
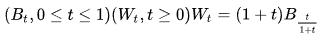
Свойство 3:
Предположим, что это обозначает стандартный броуновский мост и случайное (почти наверняка уникальное) время, когда оно достигает своего минимума. Затем процесс, определяемый законом нормированной экскурсии броуновского движения. Кроме того , не зависит от и имеет единообразный закон .
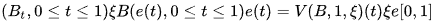
Интуитивно понятно, что нормализованная броуновская экскурсия строится из броуновского моста, разрезая его до минимума и инвертируя две полученные части.
Взаимный:
Предположим, что это обозначает нормированный ход броуновского движения и независимую случайную величину от и единого закона о . Тогда процесс, определенный с помощью закона, имеет силу броуновского моста. Кроме того, это уникальное время, когда он достигает своего минимума.
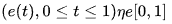 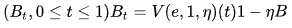
Свойство 4 (время обращения):
Пусть будет действительное число, тогда b 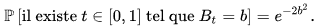
Свойство 5 (закон супремума):
Пусть - строго положительное действительное число, тогда b
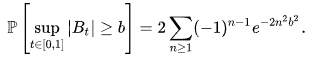
Именно это свойство лежит в основе теста Колмогорова-Смирнова .
Свойство 6:
Позвольте быть два строго положительных действительных числа, тогда a,b
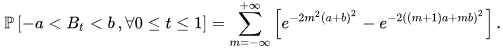
Свойство 7:
Пусть - строго положительное действительное число, тогда x
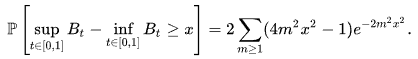
2.2 Вспомогательные связи и определения
Отношения:
Броуновский мост и броуновская экскурсия - два разных математических объекта, но один может быть построен из другого.
Определим преобразование Вервата непрерывной функции следующим образом V (ƒ, T ,ơ)ƒ: [0, T ]→ ℝ
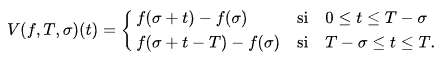
Наглядно, траектория является то , что на , но сокращение времени и где две части перепутаны. V (ƒ, T ,ơ)ƒ [0, T ]ơ
Выражение в форме диффузии:
Броуновский мост можно описать как диффузионный процесс. Действительно, если - стандартное броуновское движение, решение стохастического дифференциального уравнения : W
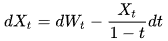
наделенный начальным условием имеет тот же закон, что и броуновский мост. В частности, процесс является марковским , что не ясно из определения как броуновское движение, обусловленное его конечным значением.
X0 = 0 XX
Связь с эмпирическим процессом:
Согласно теореме Донскера , если переменные независимы, одинаково распределены с единым законом о , эмпирический процесс
(X1 , …, Xn) [0, 1]
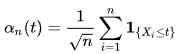
сходится по закону к Броуновскому мосту.
Заключение
Можно обобщить определение броуновского моста так, чтобы оно индексировалось классами функций. Позвольте быть классом измеримых функций, определенных на реальных значениях, и случайной величиной распределения, определенной на пространстве вероятностей со значениями в . Обозначим в броуновское -bridge индексированную этим классом функций, то есть уникальный центрированный гауссовский процесс которого корреляционная функция задается
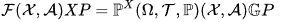 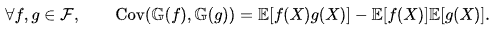
Таким образом, стандартный броуновский мост - это броуновский мост, индексируемый классом индикаторных функций.
F = { x→ 1{x≤t} : t ∈ℝ }
Если эмпирический процесс, индексированный классом функций, сходится по закону к броуновскому мосту, индексированному этим же классом функций, то этот класс называется классом Донскера. F
Список литературы
Филипп Биан, Связь между мостом и экскурсией реального броуновского движения , Анналы Анри Пуанкаре , раздел B, том 22, № 1 (1986), стр. 1-7
Р. М. Дадли , Реальный анализ и вероятность , Издательство Кембриджского университета ,2002 г.( ISBN 0-511-02958-6 )
Аспекты броуновского движения, Springer, 2008, R. Mansuy, M. Yor, стр. 2
Глассерман, Пол (2004). Методы Монте-Карло в финансовом инжиниринге. Нью-Йорк: Springer-Verlag. ISBN 0-387-00451-3.
Ревуз, Даниил; Йор, Марк (1999). Непрерывные мартингалы и броуновское движение (2-е изд.). Нью-Йорк: Springer-Verlag. ISBN 3-540-57622-3.
|
 Скачать 267.6 Kb.
Скачать 267.6 Kb.