маткад. Маткад 1-33 67-100. В чем состоит свойство унимодальности функций

• Название: В чем состоит свойство унимодальности функций
• Анкор: маткад
• Дата: 24.04.2023
• Размер: 2.46 Mb.
• Имя файла: Маткад 1-33 67-100.docx
• Тип: Документы; #1084533
• страница: 1 из 5

1. 
   В чем состоит свойство унимодальности функций?
   

Если функция f x( ), определенная на множестве U, имеет, кроме глобального, еще и локальные минимумы, отличные от него, то минимизация f x( ), как правило, сильно затрудняется. Большинство методов поиска минимума f x( ) приспособлено только для тех функций, у которых каждый локальный минимум является одновременно и глобальным. Этим свойством обладают унимодальные функции. Основные свойства унимодальных функций:

1. Любая из точек локального минимума унимодальной функции является и точкой ее глобального минимума на отрезке [а; b].

2. Функция, унимодальная на отрезке [а; b], является унимодальной и на любом меньшем отрезке [с; d]   [а; b].

3. Пусть f (x)  Q [а; b] и  . Тогда:

если  , то x^*   [a; x₂] ;

если  , то x^*   [x₁; b],

где х* - одна из точек минимума f (x) на отрезке [a; b].

2. 
   Сформулируйте утверждение, на которое опираются все методы одномерной минимизации.
   

Одно из важнейших направлений в конструировании изделий, а также проектировании и эксплуатации технологических процессов состоит в оптимизации (минимизации или максимизации) некоторой характеристики f(x) Функцию f(x) часто называют целевой функцией. Заметим, что основное внимание может быть уделено минимизации целевой функции, так как максимизация сводится к минимизации с помощью введения новой целевой функции f(x)=-f(x). В случае, когда варьируется один скалярный параметр х, возникает задача одномерной минимизации.

Необходимость изучения методов решения задачи одномерной минимизации определяется не только тем, что задача может иметь самостоятельное значение, но и в значительной мере тем, что алгоритмы минимизации являются существенной составной частью алгоритмов решения задач многомерной минимизации , а также других вычислительных задач. Применение некоторых методов одномерной минимизации возможно только в случае, если скорость изменения целевой функции f(х) на любом участке отрезка [а; b] ограничена некоторым числом, одним и тем же для всех участков. В этом случае говорят, что f(х) удовлетворяет на отрезке [а; b] условию Липшица.

3. 
   Опишите алгоритм, позволяющий найти начальный отрезок локализации минимума.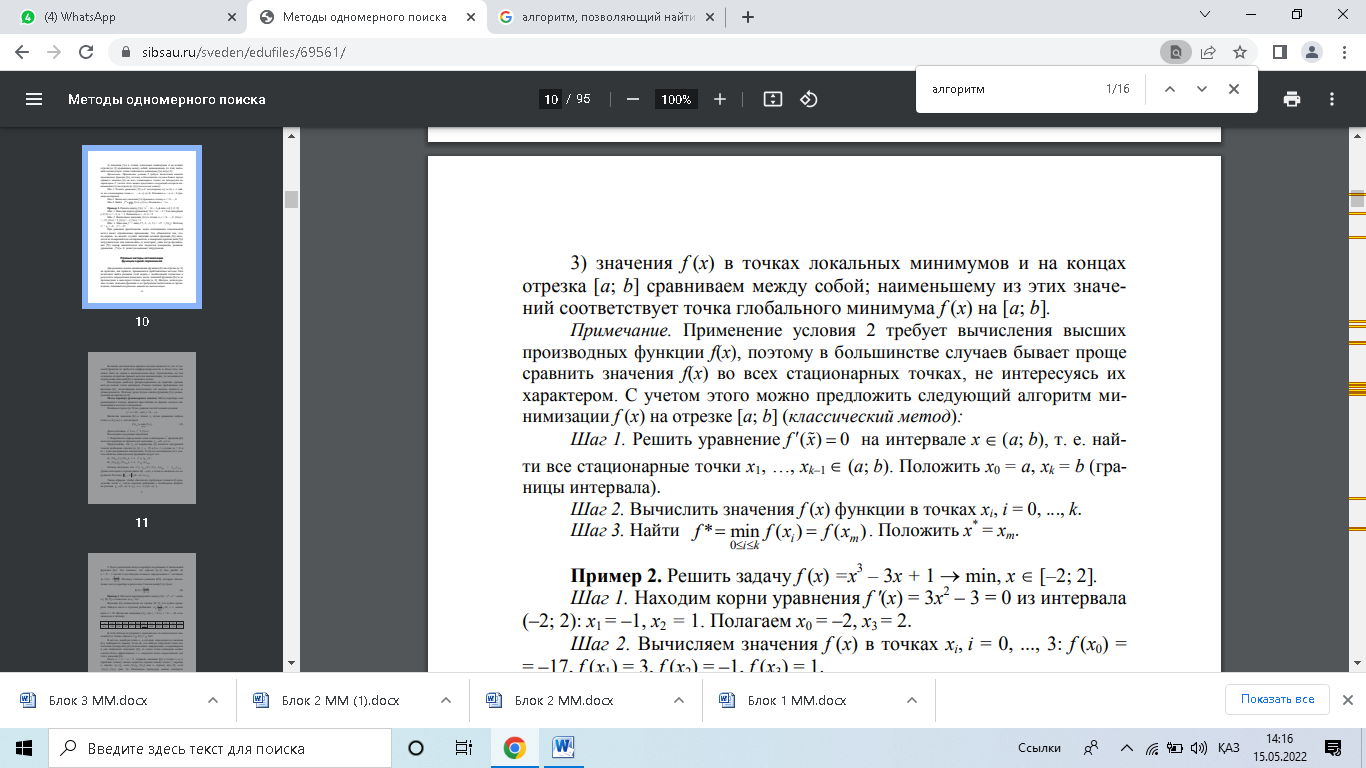
   

4. 
   Назовите преимущества и недостатки методов дихотомии, Фибоначчи и золотого сечения.
   

Существует довольно очевидная теорема: "Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но м.б. и несколько)". На базе этой теоремы построено численное нахождение приближенного значения корня функции. Обобщенно этот метод называется дихотомией, т.е. делением отрезка на две части. Дихотомическое деление имеет недостаток: при делении объё­ма понятия на два противоречащих понятия каждый раз остаётся крайне неопределённой та его часть, к которой относится части­ца «не». Если разделить учёных на историков и не историков, то вторая группа оказывается весьма неясной. Кроме того, если в начале дихотомического деления обычно довольно легко устано­вить наличие противоречащего понятия, то по мере удаления от первой пары понятий найти его становится всё труднее.

Метод Фибоначчи (англ. Fibonacci method) — это улучшение реализации поиска с помощью золотого сечения, служащего для нахождения минимума/максимума функции. Подобно методу золотого сечения, он требует двух вычислений функции на первой итерации, а на каждой последующей только по одному. Однако этот метод отличается от метода золотого сечения тем, что коэффициент сокращения интервала неопределенности меняется от итерации к итерации.

Метод дихотомии, как видно из его описания обеспечивает наименьшее количество итераций, необходимых для достижения заданной точности. При этом на каждой итерации метода вычисляются два значения функции (в точках сk и dk ). Однако эффективность метода прямого поиска характеризуется не количеством итераций, а количеством вычисленных значений функции. Существуют методы, в которых на каждой итерации вычисляется только одно значение функций. Количество итераций в них больше, чем в методе дихотомии, но общее количество вычисленных значений функции может быть и меньше.

5. 
   В чем состоит суть интерполяционных методов минимизации?
   

Интерполяция — это метод нахождения неизвестных промежуточных значений некоторой функции по имеющемуся дискретному набору ее известных значений. Типичным примером такой функции является временной ряд, значения которого — это наблюдения, зафиксированные через определенный интервал времени.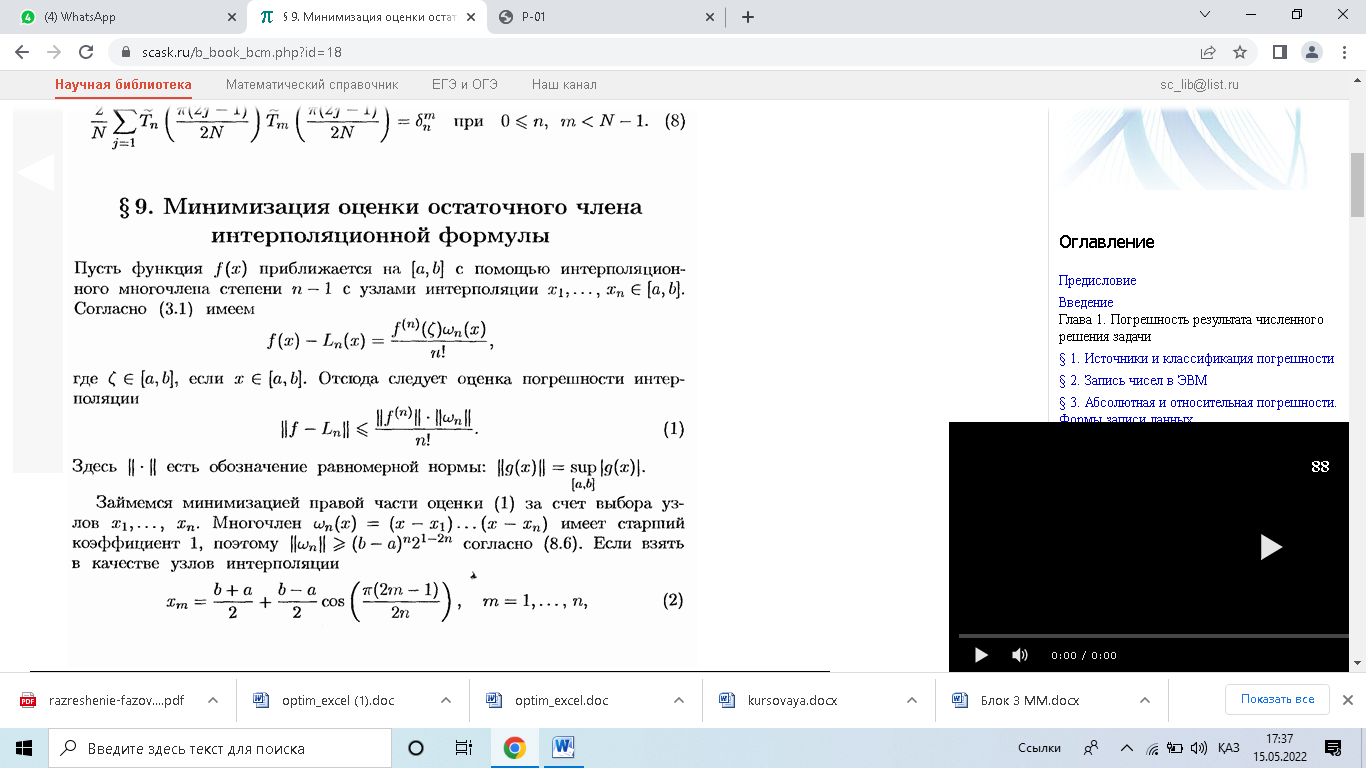

6. 
   Дайте определение направления убывания. Сформулируйте необходимые и достаточные условия направления убывания.
   

Многие методы мини­мизации относятся к числу методов спуска. В методах спуска на­правление движения к минимуму на каждом шаге выбирается из числа направлений убывания минимизируемой функции.

Говорят, что вектор h задает направление убывания функции f в точке x, если f(x + ah) < f(x) при всех достаточно малых a > 0. Сам вектор h также называют иногда направлением убывания. Мно­жество всех направлений убывания функции f в точке х будем обо­значать через U(х, f).

Таким образом, если любой достаточно малый сдвиг из х в на­правлении вектора h приводит к уменьшению значения функции f, то h Î U(x, f).

Заменив неравенство, фигурирующее в определении направления убывания, на противоположное, получим определение направления возрастания.

В дальнейшем нам понадобятся следующие достаточный и необ­ходимый признаки направления убывания.

7. 
   В чем состоит общая идея методов спуска? Укажите хотя бы один метод, являющийся методом спуска.
   

Все методы спуска решения задачи безусловной минимизации различаются либо выбором направления спуска, либо способом движения вдоль направления спуска. Это позволяет написать общую схему методов спуска. Метод градиентного спуска.

Одним из самых распространённых методов минимизации, связанных с вычислением градиента, является метод спуска по направлению антиградиента минимизируемой функции. В пользу такого выбора направления спуска можно привести следующие соображения. Поскольку антиградиент, то есть j ’(xk) в точке xk указывает направление наискорейшего убывания функции, то естественным представляется сместиться из точки xk по этому направлению. радиентный спуск — метод нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.

Наиболее простой в реализации из всех методов локальной оптимизации. Имеет довольно слабые условия сходимости, но при этом скорость сходимости достаточно мала (линейна). Шаг градиентного метода часто используется как часть других методов оптимизации, например, метод Флетчера — Ривса.

8. 
   Что такое моно - и мультимодальные функции?
   

Оптимизация функций — это область исследований, где поставлена задача найти некое входное значение [аргумент функции], результат которого — максимум или минимум данной функции. Алгоритмов оптимизации много, поэтому важно развивать алгоритмическое чутьё и исследовать алгоритмы на простых и легко визуализируемых тестовых функциях. Унимодальность означает, что функция имеет единственный глобальный оптимум.Унимодальная функция может быть выпуклой и невыпуклой. Выпуклая функция — это функция, на графике которой между двумя любыми точками можно провести линию и эта линия останется в домене. В случае двумерной функции это означает, что поверхность имеет форму чаши, а линии между двумя точками проходят по чаше или внутри неё. Давайте рассмотрим несколько примеров унимодальных функций.

Мультимодальная функция — это функция с более чем одной “модой” или оптимумом (например долиной на графике). Мультимодальные функции являются невыпуклыми. Могут иметь место один или несколько ложных оптимумов

9. 
   Определите хотя бы один отрезок унимодальности функции f (x) = x − 2x2 + 0,2x5.
   

1. Находим интервалы возрастания и убывания. Первая производная.

f'(x) = x4-4·x+1

Находим нули функции. Для этого приравниваем производную к нулю

x4-4·x+1 = 0

Откуда:

x1 = 0.25099

x2 = 1.4934

x3 = 0.25099216

(-∞ ;0.25099216)	(0.25099216; 0.25099)	(0.25099; 1.4934)	(1.4934; +∞)
f'(x) > 0	f'(x) < 0	f'(x) < 0	f'(x) > 0
функция возрастает	функция убывает	функция убывает	функция возрастает

В окрестности точки x = 0.25099216 производная функции меняет знак с (+) на (-). Следовательно, точка x = 0.25099216 - точка максимума. В окрестности точки x = 1.4934 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1.4934 - точка минимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

f''(x) = 4·x3-4

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

4·x3-4 = 0

Откуда точки перегиба:

x1 = 1.0

(-∞ ;1.0)	(1.0; +∞)
f''(x) < 0	f''(x) > 0
функция выпукла	функция вогнута

10. 
    Минимизируйте функцию ƒ(х) = 3х2 + 12/х3 − 5 на отрезке 0,5 ≤ х ≤ 2,5, используяа) метод дихотомии, б) метод золотого сечения, в) метод Фибоначчи, г) метод парабол. В каждом случае проведите по четыре вычисления значений функции. Сравните результирующие отрезки локализации минимума.
    

f(x) = 3•x2+12/x3-5
Используем для этого Метод золотого сечения.
Решение.
Положим a1 = a, b1 = b. Вычислим λ1 = a1 + (1- 0.618)(b1 - a1)=1.264, μ1 = a1 + 0.618(b1 - a1) = 1.736.
Вычислим f(λ1) = 5.7352, f(μ1) = 6.3348
Итерация №1.
Поскольку f(λ1) < f(μ1), то b2 = 1.736, a2 = a1, μ2 = 1.264, f(μ2)=6.3348
λ2 = a2 + (1-0.618)(b2 - a2) = 0.5 + (1-0.618)(1.736 - 0.5) = 1.264, f(1.264) = 5.7352
Итерация №2.
Поскольку f(λ2) > f(μ2), то a3 = 0.9722, b3 = b2, λ3 = 1.264, f(λ3)=10.8963
μ3 = a3 + 0.618(b3 - a3) = 0.9722 + 0.618(1.736 - 0.9722) = 1.4442, f(1.4442) = 5.7352
Итерация №3.
Поскольку f(λ3) > f(μ3), то a4 = 1.264, b4 = b3, λ4 = 1.4442, f(λ4)=5.7352
μ4 = a4 + 0.618(b4 - a4) = 1.264 + 0.618(1.736 - 1.264) = 1.5557, f(1.5557) = 5.241
Итерация №4.
Поскольку f(λ4) < f(μ4), то b5 = 1.5557, a5 = a4, μ5 = 1.4442, f(μ5)=5.4478
λ5 = a5 + (1-0.618)(b5 - a5) = 1.264 + (1-0.618)(1.5557 - 1.264) = 1.4442, f(1.4442) = 5.241

|5.2384-5.2384|≤0.001
Находим x как середину интервала [a,b]:
x=(1.4313+1.4304)/2=1.4308140069917
Ответ: x = 1.4308140069917; F(x) = 5.2384

Используем для этого Метод Фибоначчи.
Важнейшая особенность этого метода состоит в том, что он позволяет для заранее заданного числа вычислений функции построить оптимальную процедуру поиска минимума унимодальной функции.
Предположим, что заданный начальный интервал неопределенности [a₁,b₁], [a_i,b_i] является интервалом неопределенности, полученным на i-той итерации. Рассмотрим две точки λ_i и μ_i из интервала [a_i,b_i], заданные с помощью соотношений:


где n - заданное число вычислений функции; Fk - последовательность чисел Фибоначчи, заданная с помощью рекуррентной формулы:
F_k+1 = F_k + F_k-1, k = 1,2, … , где F₀ = F₁ = 1
Новый интервал неопределенности (a_i+1,b_i+1) равен (λ_i,b_i), если f(λ_i) > f(μ_i), и равен (a_i, μ_i), если f(λ_i) < f(μ_i). Тогда в первом случае, новый интервал неопределенности имеет длину:

Отсюда следует, что в любом случае на i-той итерации интервал неопределенности сжимается в F_n-i/F_n-i+1 раз. На (i+1)-ой итерации либо λ_i+1 = μ_i, либо μ_i+1 = λ_i. Поэтому на каждом шаге вычисляется только одно новое значение функции. На (n-1)-ой итерации λ_n-1 = μ_n-1,и значение функции не вычисляется.
Если ε есть точность вычисления значения функции, n – максимально возможное число вычислений функции, то конечный интервал неопределенности будет равен:

Решение.
Последовательность чисел Фибоначчи имеет вид: 1,1,2,3,5,8,13,21,34,55,89,144,
Итерация 1.
Вычислим точки


f(λ₁) = 5.7349; f(μ₁) = 6.3345
Так как f(λ₁) < f(μ₁), то сокращаем интервал неопределенности и принимаем на 2-й итерации:
a₂ = a₁ = 0.5; b₂ = μ₁ = 1.736
Итерация 2.
Вычислим точки


f(λ₂) = 10.9047; f(μ₂) = 5.7349
Так как f(λ₂) > f(μ₂), то сокращаем интервал неопределенности и принимаем на 3-й итерации:
a₃ = λ₂ = 0.97191011235955; b₃ = b₂ = 1.736