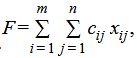маткад. Маткад 1-33 67-100. В чем состоит свойство унимодальности функций

• Название: В чем состоит свойство унимодальности функций
• Анкор: маткад
• Дата: 24.04.2023
• Размер: 2.46 Mb.
• Имя файла: Маткад 1-33 67-100.docx
• Тип: Документы; #1084533
• страница: 4 из 5

Решение.
Находим первую производную функции:

Приравниваем ее к нулю:


x₁ = 0

Вычисляем значения функцииf(0) = 0

Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
или
Вычисляем:

y''(0) = 2>0 - значит точка x = 0 точка минимума функции.

y = x-2·sin(x²)
Необходимое условие экстремума функции одной переменной.
Уравнение f'₀(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f'₀(x*) = 0
f''₀(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f'₀(x*) = 0
f''₀(x*) < 0
то точка x* - локальный (глобальный) максимум.
Решение.
Находим первую производную функции:

y' = -4·x·cos(x²)+1

Приравниваем ее к нулю:

-4·x·cos(x²)+1 = 0

x₁ = 0.25

x₂ = 3.327

Вычисляем значения функции

f(0.25) = 0.125

f(3.327) = 5.322

Ответ:f_min = 0.125, f_max = 5.322

Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:

y'' = 8·x²·sin(x²)-4·cos(x²)

Вычисляем:

y''(0.25) = -3.961<0 - значит точка x = 0.25 точка максимума функции.

y''(3.327) = -88.616<0 - значит точка x = 3.327 точка максимума функции.

25. 
    В чем состоит суть метода параметрической идентификации?
    

Как уже указывалось выше, число работ и разнообразие методов идентификации делает практически невозможной достаточно полную их характеристику. Одним из рациональных подходов в этих условиях является отбор методов параметрической идентификации по их целевой направленности, т. е. зависимости от свойств объектов, отражением которых являются модели определенных предложена, например, следующая классификация моделей под этим углом зрения:

• 
  статические или динамические;
  
• 
  детерминированные или стохастические;
  
• 
  линейные или нелинейные;
  
• 
  непрерывные или дискретные.
  

26. 
    Охарактеризуйте особенности идентификации стохастических и динамических моделей.
    

Простейшим входным сигналом, используемым при идентификации, является ступенчатый сигнал. Такой сигнал на входе системы может быть сформирован, например, путем внезапного открывания (или закрывания) входного клапана, включения (или выключения) управляющего напряжения или тока и т.д., так как это почти всегда возможно без применения специальной аппаратуры. У идеального ступенчатого сигнала время нарастания сигнала равно нулю, что физически невозможно, так как при этом скорость нарастания должна быть бесконечно большой. Следовательно, любой реальный ступенчатый входной сигнал является лишь аппроксимацией идеального ступенчатого сигнала. Однако, если время нарастания сигнала гораздо меньше периода высшей гармоники, то ошибка идентификации становится незначительной. В процессах с помехами или в случаях, когда измерения содержат шум (что обычно имеет место на практике), необходима соответствующая фильтрация шума.

Идентификация с помощью переходной функции проводится автономно, вне процесса управления, и поэтому применима только к стационарным процессам. Однако, поскольку ступенчатые возмущения воздействуют на многие системы во время включения или в процессе нормальной работы, то переходные функции можно записать, не нарушая нормального режима работы системы. В этом заключается дополнительное преимущество рассматриваемого метода. Очевидно, что при этом необходимо предположить, что система стационарная, так как результаты идентификации считаются достоверными и после приложения ступенчатого сигнала. Кроме того, предполагается, что в диапазоне амплитуд ступенчатого сигнала система линейна.

Во многих случаях для определения передаточной функции системы можно использовать запись ее переходной функции. Такой способ применим к большинству типов линейных систем (1 и 2 порядков и к апериодическим системам высшего порядка). Наиболее корректно графический метод идентификации с использованием переходных функций применяется  к процессам первого порядка.

27. 
    Что является критерием идентичности модели и объекта?
    

При решении практических задач, в том числе при идентификации технологического процесса, не представляется возможным учесть в модели все переменные и все внутренние связи между многочисленными переменными. Поэтому построение модели осуществляется по относительно небольшому количеству переменных. Выбор этих переменных определяется целью построения модели, наличием технических средств передачи и обработки необходимой информации, уровнем теории, имеющимися алгоритмами и математическим обеспечением.

Четко сформулированные цели и требования к системе управления технологическим процессом являются той основой, которая должна быть обеспечена строящейся моделью.

Для того чтобы можно было судить о том, какая построена модель, удовлетворяет ли она предъявляемым к ней требованиям, необходимо уметь количественно оценить уровень наших знаний о технологическом процессе, степень соответствия модели реальному процессу. С этой целью вводится количественная мера степени идентичности ( адекватности, изоморфности) модели реальному процессу, объекту. При построении такой меры, естественно, стремятся к тому, чтобы она базировалась на тех характеристиках, которые используются при идентификации объекта, и могла быть определена по этим характеристикам или непосредственно по данным "вход-выход".

Особенностью технологического процесса, как уже отмечалось, является вероятностный характер. Все измеряемые входные переменные не определяют однозначно выхода объекта. Степень идентичности модели для разных объектов различна, но никогда не достигает единицы. Это является следствием многих причин: недостаточной изученности процесса, отсутствия точного математического описания, отсутствия необходимых датчиков для измерения технологических параметров. Степень связи, т.е. отношение условной дисперсии выхода относительно всех входных переменных к дисперсии выходной величины колеблется от 0, 3 до 0, 95 и редко бывает больше. Таким образом, остаточная дисперсия, т.е. дисперсия выхода, при применении идеальной системы управления не равна нулю. Остаточная дисперсия для физических моделей значительно больше, чем для моделей, полученных с помощью методов идентификации.

28. 
    Что такое адаптивная и неадаптивная идентификация?
    

Адаптивная идентификация проводится непрерывно, в режиме on-line. Она представляет собой процесс построения модели объекта в виде аналитической зависимости на основании сведений о значении искомой функции и ее аргументов. В качестве функции может выступать любой искомый обобщенный показатель, а в качестве аргументов - величины координат в пространстве состояний, параметры и показатели. Предполагается, что значения функции определяются значениями ее аргументов. Параметры зависимости функции от своих аргументов находятся автоматически по известным алгоритмам (рис.16.2). Никаких предварительных соображений о структуре зависимости функции от ее аргументов и параметров запаздывания не требуется. Интенсивное развитие методов идентификации обусловлено с одной стороны возрастающими возможностями средств вычислительной техники, а с другой стороны системным подходом к решению этой проблемы, включающим информационные, структурные и математические аспекты анализа, которые составляют основу адаптивных методов идентификации

29. 
    Что является предметом структурной идентификации?
    

Структурная идентификация включает в себя следующие задачи: Выделение объекта из окружающей его и взаимодействующей с ним среды. Ранжирование входов и выходов объекта по степени их влияния на поведение объекта. Определение оптимального числа входов и выходов объекта, учитываемых в модели

30. 
    Какие задачи необходимо решить при выборе структуры объекта?
    

Цель идентификации — установить тождественность или подлинность объекта (товара) его основополагающим характеристикам.

На современном этапе задачами идентификации являются:

• определение структуры, норм и правил в области идентификации товаров;

• разработка основополагающих критериев, пригодных для целей идентификации однородных групп, конкретных видов и наименований товаров;

• исследование потребительских свойств товаров и показателей, их характеризующих, для выявления наиболее достоверных критериев идентификации;

• совершенствование стандартов, ТУ и другой нормативной документации путем включения в нее показателей качества для целей идентификации;

• совершенствование методов идентификации товаров, и в первую очередь экспресс-методов, позволяющих с достаточно высокой степенью достоверности определять все основополагающие характеристики товаров, особенно товароведные.

Объектами идентификации являются продукция, услуги, ценные бумаги (деньги, акции, векселя и др.), информация, рабочая сила и другие объекты коммерческой деятельности. В данном учебном пособии разберем лишь одну группу объектов — продукцию, которая вовлекается в процесс купли-продажи и становится товаром. Именно об идентификации продовольственных товаров в сфере торговли и у потребителя, приобретающего товары, пойдет речь, хотя следует отметить, многие рассматриваемые вопросы в равной степени могут быть отнесены и к непродовольственным товарам.

31. 
    Какова цель параметрической идентификации?
    

Параметрическая идентификация — определяются значения параметров модели. Методы идентификации: Активные (можно подавать на вход объекта тестовые сигналы) и пассивные. Детерменированые и статистические (учитывают наличие шума). Оперативные (идентификация проходит “налету”) и ретроспективные. Целью данного этапа является построение адекватной модели системы в общем контексте решения исходной проблемы. Задача параметрической идентификации сводится к отысканию таких оценок параметров модели, которые обеспечивают наибольшую, в каком либо смысле близость значений на выходе, рассчитанных по модели и, полученных в эксперименте, при одинаковом значении входных данных.

32. 
    Что такое функция локальной невязки?
    

Невязка — величина ошибки (расхождения) приближённого равенства.

Если точное решение неизвестно, можно использовать аппроксимацию решения с небольшой невязкой.Невязка фигурирует во многих разделах математики, в том числе в итерационных методах, таких как метод обобщенного минимума, в котором решение системы уравнений находится путём минимизации невязки.В навигации невязкой называется расстояние между вычисленным по прокладке местоположением судна и фактически определённым (по светилам, маякам и т.д.) местоположением, измеряется в морских милях

33. 
    Какие критерии могут быть использованы в качестве суммарной невязки?
    

Невязка — величина ошибки (расхождения) приближённого равенства. Пусть требуется найти такое x, что значение функции: Если точное значение x неизвестно, вычисление ошибки невозможно, однако при этом может быть определена невязка. Суммарная невязка представляет собой сумму этих функций и является результатом их интерференции. Функцию распределения суммарной невязки можно получить следующим образом. Вначале получим плотность вероятности квадрата одной случайной величины, а затем по закону сложения случайных величин можно получить искомую плотность вероятности. Для вычисления функции распределения квадрата суммарной невязки воспользуемся характеристическими функциями

34. 
    При каком значении относительной невязки модель считается адекватной?
    

Если относительная невязка меньше предельно допустимой, то производят увязку приращения, заключающуюся в изменении величины каждого приращений с таким расчетом, чтобы алгебраическая сумма всех приращений получилась равной нулю. Для этого 2 Дх и 2Ду распределяют с обратным знаком между приращениями пропорционально длине сторон.  [4]

Если относительная невязка допустима, то вычисленные приращения увязывают, вводя в них поправки. 

1. 
   Сформулируйте общую задачу линейного программирования
   

Линейное программирование (ЛП) – это раздел математики, в котором изучаются методы решения задач на отыскание экстремумов линейных функций многих переменных при наличии линейных ограничений, наложенных на переменные.

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции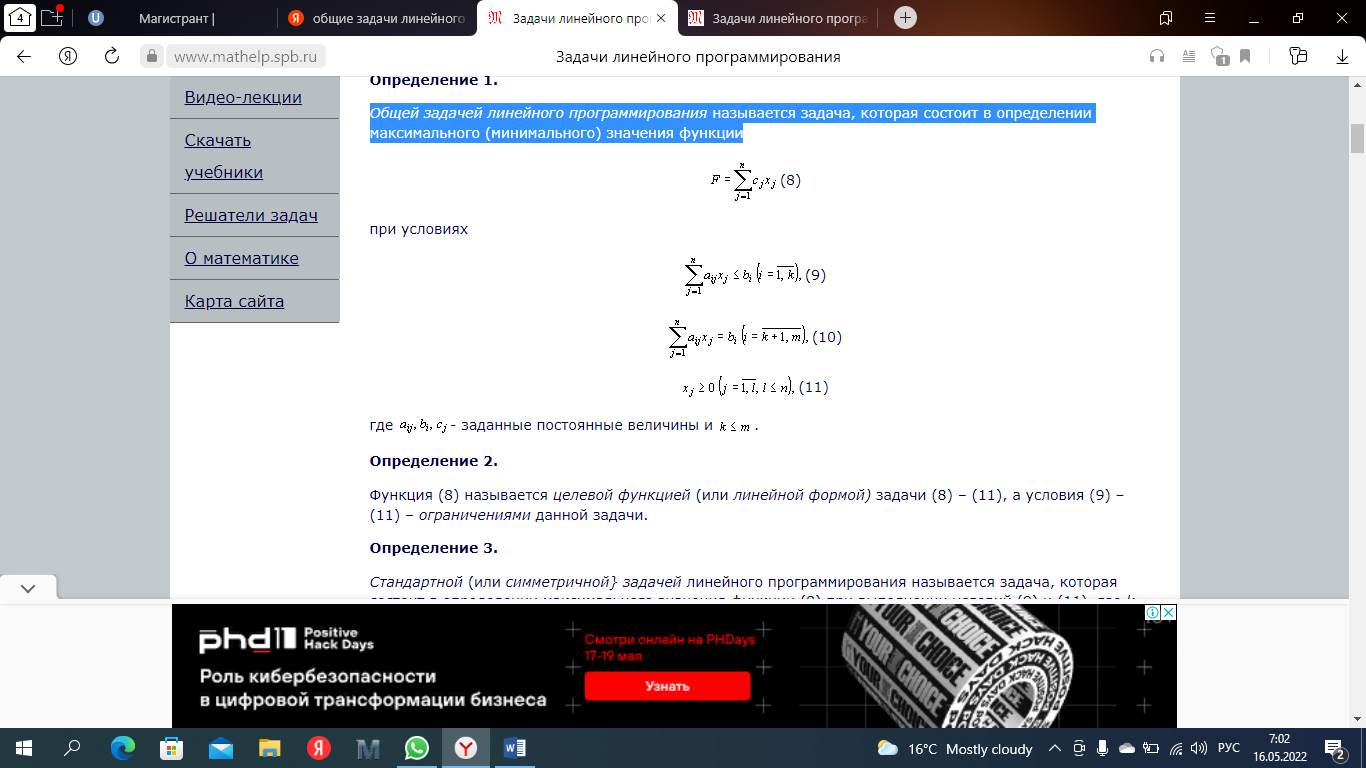



Определение 2.Функция (8) называется целевой функцией (или линейной формой) задачи (8) – (11), а условия (9) – (11) – ограничениями данной задачи.

Определение 3.Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n.

Определение 4.Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где k = 0 и l = п.

Определение 5.Совокупность чисел  ,удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).

Определение 6.План  , при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.

Значение целевой функции (8) при плане Х будем обозначать через  . Следовательно, X^* – оптимальный план задачи, если для любого Х выполняется неравенство  [соответственно  ].

2. 
   Чем отличается основная задача линейного программирования от общей?
   

общая задача линейного программирования – это задача, в которой требуется найти максимум или минимум (оптимум) функции, называемой функцией цели, при ограничениях, заданных системой линейных неравенств или уравнений.

Основная задача линейного программирования отличается от задачи программирования общего вида тем, что ограничения в ней заданы в виде системы уравнений: Из курса линейной алгебры известно, что такая система либо не имеет решений, либо имеет единственное решение или бесчисленное множество решений. Будем полагать, что оптимальное решение единственно, хотя на практике их может быть несколько. Если система не имеет решений, ее анализируют повторно, в соответствии с имеющейся конкретной практической ситуацией. Те уравнения, которые являются причиной отсутствия решений, исключаются из системы.

3. 
   Чем отличается общая задача линейного программирования от канонической?
   

Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные xj налагаются условия неотрицательности, то она называется задачей линейного программирования в канонической форме или канонической задачей линейного программирования (КЗЛП).

Общая задача линейного программирования – это задача, в которой требуется найти максимум или минимум (оптимум) функции, называемой функцией цели, при ограничениях, заданных системой линейных неравенств или уравнений.

Отличие КП от ОЗ в канонической форме записи задач линейного программирования все переменные, входящие в систему ограничений, должны быть неотрицательными.

4. 
   Какие ограничения называют жесткими (нежесткими)?
   

Жесткость и нежесткость ограничений ЛП [hardness and slackness of LP constraints] — характеристика ограничений задачи линейного программирования по степени их влияния на оптимум (см. Чувствительность оптимального решения). Ограничение является нежестким, когда малые изменения константы ограничения не отражаются на решении задачи. Например, в распределительной задаче это означает, что спрос строго меньше предложения, в результате чего объективно обусловленные оценки равны нулю. Решение не зависит от общего объема возможного предложения товара, так как имеющееся количество его превышает ту потребность в нем, которая соответствует его использованию в оптимальной точке.

Ограничение является жестким, когда любое малое изменение константы (параметра) ограничения приводит к изменению значения целевой функции (то есть объективно обусловленная оценка не равна нулю).

5. 
   Приведите примеры существенных и несущественных ограничений.
   

Существенные и несущественные свойства математических объектов раскрываются в процессе определения понятий математики. Множество существенных свойств составляют содержание понятия.

Под существенными свойствами будем понимать те, без которых понятие не существует, и при помощи которых выделяются объекты интересующего нас множества. Существенные свойства – это всегда общие свойства, но обратное неверно – общие свойства могут быть несущественными. Так, в школьных учебниках в уравнениях преобладает обозначение переменной – “х”. Это свойство общее, но не существенное.
Кроме того, понятия “существенное” и “несущественное” свойство относительны, в разных ситуациях одно и то же свойство математического объекта может быть как существенным, так и несущественным. Например, при выделении линейных функций среди других знак коэффициента при х – несущественное свойство, но оно же становится существенным при выделении среди линейных функций возрастающих.

6. 
   Чем отличается выпуклый многогранник от выпуклого многогранного множества?
   

Выпуклый многогранник разрезает пространство на две части – внешнюю и внутреннюю. Внутренняя его часть есть выпуклое тело. Обратно, если поверхность выпуклого тела многогранна, то соответствующий многогранник –выпуклый. Теорема. Сумма всех плоских углов выпуклого многогранного угла меньше 360 градусов.

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

Общим определяющим свойством, которое отличает выпуклый многоугольник от невыпуклого, является то, что если взять любые две его точки и соединить их отрезком, то весь отрезок будет принадлежать этому многоугольнику. Это свойство может быть принято за определение выпуклого множества точек.

7. 
   Дайте определение угловой точки выпуклого многогранного множества.
   

Вектор X, принадлежащий выпуклому множеству V, называют крайней или угловой точкой или вершиной V, если для любых векторов X(1) и X(2) из V при 0≤λ≤1 из того, что X = (1 - λ)X(2) + λX(1), следует, что X = X(1) = X(2). Иначе, X - крайняя (угловая) точка множества V, если X нельзя представить в виде выпуклой комбинации каких-либо двух других точек из V, от нее отличных.
Геометрически это означает, что крайняя точка не может лежать внутри какого-либо отрезка, принадлежащего множеству V.

8. 
   Сформулируйте основную теорему линейного программирования.
   

(основная теорема линейного программирования):

1) Линейная форма достигает своего минимума в угловой точке многогранника решений.

2) Если она принимает минимальное решение более чем в одной угловой точке, то она достигает того же самого значения в любой точке, являющейся выпуклой комбинацией этих угловых точек.

Теорема 1: Множество всех допустимых решений системы ограничений задачи линейного программирования, является выпуклым.
Теорема 2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , где n - число неизвестных , а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.
Теорема 3: Если известно, что система векторов в разложении линейно независима и такова, что , где , то точка является угловой точкой многогранника решений.
Теорема 4: Если - угловая точка многогранника решений, то векторы в разложении , соответствующие положительным, являются линейно независимыми.
Следствие 1: Так как векторы имеют размерность m, то угловая точка многогранника решений имеет не более m положительных компонент .
Следствие 2: Каждой угловой точке многогранника решений соответствует линейно независимых векторов системы векторов .

Эта теорема имеет важнейшее значение, так как она указывает путь решения задачи линейного программирования. Совсем не надо перебирать все точки допустимой области. Достаточно перебрать вершины допустимой области, а ведь их - конечное число. Кроме того, как это окажется далее, не нужно перебирать все вершины, можно этот перебор существенно сократить. 

9. 
   В чем заключается первая геометрическая интерпретация задачи линейного программирования?
   

Определение 1. Значения неизвестных переменных, удовлетворяющие всем ограничениям задачи линейного программирования, называются допустимыми значениями переменных или планами.

Определение 2. Множество всех планов задачи линейного программирования называется областью допустимых значений переменных (ОДЗ).

Определение 3. План задачи линейного программирования, при котором целевая функция принимает минимальное (или максимальное) значение на ОДЗ называется оптимальным.
Графическим методом в основном решаются задачи с малым числом переменных. Он включает следующие этапы:

1) Находятся геометрические решения всех ограничений задачи.

2) Областью допустимых значений будет многоугольник, полученный с помощью пересечения всех полуплоскостей.

Таким образом, геометрически решить задачу линейного программирования означает найти среди всех точек ОДЗ такую точку (точки), при которой (которых) целевая функция принимает своё экстремальное значение.

Замечание. При нахождении решения задачи линейного программирования графическим методом могут встретиться случаи, изображенные на следующих рисунках.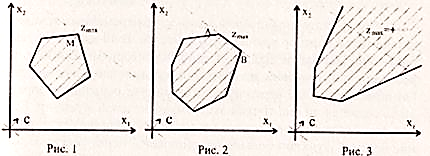



 

На первом рисунке изображен случай, когда целевая функция принимает максимальное значение в единственной точке М. Из второго рисунка видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ. На третьем рисунке изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений.

Отметим, что нахождение минимального значения целевой функции отличается от нахождения её максимального значения лишь тем, что линия уровня 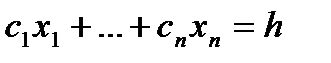  перемещается не в направлении вектора с, а в противоположном направлении.

Графический метод является наглядным и простым методом решения задач линейного программирования. Однако область его применения ограничена размерностью задачи. Если задача представлена в стандартной форме, то количество переменных должно быть не более трёх.

10. 
    В чем состоит идея геометрического метода решения задачи линейного программирования? Для каких задач он применим?
    

Геометрический метод решения ЗЛП применяется в случае, если задача содержит не более двух переменных или может быть сведена к таковой. Каждое из неравенств системы ограничений геометрически определяет полуплоскость допустимых значений переменных с граничными прямыми. Алгоритм геометрического метода: 1. В системе ограничений знаки неравенств заменяются на знаки точных равенств и по полученным уравнениям строятся прямые на плоскости x 1 Ox 2.

Геометрические методы обычно применяются для решения двумерных задач линейного программирования, и они основаны на двух важных геометрических свойствах этих задач:

1) областью допустимых решений задачи является выпуклый многоугольник;

2) целевая функция возрастает при движении по направлению ее вектора-градиента.

11. В чем заключается вторая геометрическая интерпретация задачи линейного программирования?

Векторная форма записи КЗЛП и ее применение. Рассмотрим каноническую задачу линейного программирования 



Обозначим через аj столбцы матрицы А и будем рассматривать их как векторы пространства Rm. Тогда каждому допустимому плану КЗЛП — n-мерному вектору х — соответствует неотрицательная линейная комбинация столбцов аj, равная столбцу bÎ Rm:

Такое представление ограничений КЗЛП обычно называют векторной формой записи.

Векторы аj, j Î l:n будем называть векторами требований задачи (D, f), а вектор b — вектором ограничений. Множество всех неотрицательных линейных комбинаций столбцов аj  с геометрической точки зрения может быть представлено как многогранный выпуклый конус, натянутый на систему векторов аj  в пространстве Rm (рис. 1.3).

Соответственно, вопрос о существовании допустимого плана задачи (D, f) равнозначен вопросу о принадлежности вектора b данному конусу, а компоненты хj некоторого допустимого плана х Î D являются не чем иным, как коэффициентами разложения вектора ограничений задачи b по векторам, требований аj.

Такоепредставление КЗЛП получило название второй геометрической интерпретации.

11. 
    Дайте определения следующих понятий: опорная точка (опорный план) допустимого множества, базис опорной точки, базисные переменные.
    

Опорным планом (решением) задачи линейного программирования называется допустимый план, для которого векторы условий, соответствующие его положительным координатам, линейно независимы.

Базис - мерного пространства - совокупность любых линейно-независимых векторов .

Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.

Базисные переменные– это переменные задачи ЛП в канонической форме, которые в рассматриваемом опорном плане, не являются свободными. Они имеют неотрицательные значения, которые определяются из решения системы уравнений (

12. 
    Дайте определение двойственной задачи линейного программирования.
    

Под двойственной задачей понимается вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий прямой задачи. Заинтересованность в определении оптимального решения прямой задачи путём решения двойственной к ней задачи обусловлена тем, что вычисления при решении ДЗ могут оказаться менее сложными. Трудоёмкость вычислений при решении ЗЛП в большей степени зависит от числа ограничений, а не от количества переменных.

Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения прямой задачи и соотношения двойственной задачи являются неравенствами вида « «. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.

Двойственная задача тесно связана задачей линейного программирования. Задача первоначальная называется исходной. Решение двойственной задачи может быть получено из решения исходной и наоборот. Связующим фактом этих двух задач являются коэффициенты Cj функции исходной задачи. Данные коэффициенты называются свободными членами системы ограничений двойственной задачи. Коэффициенты Bi системы ограничений исходной задачи называются коэффициентами двойственной задачи. Транспонированная матрица коэффициентов системы ограничений исходной задачи является матрицей коэффициентов системы ограничений двойственной задачи.

13. 
    Каким свойством обладает отношение двойственности?
    

теорема двойственности. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций совпадают . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива. ... Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, то есть равенство общей оценки продукции и ресурсов обусловливает убыточность всякого другого плана, отличного от оптимального.

14. 
    Перечислите основные свойства пары двойственных задач (теоремы двойственности).
    

Двойственность является фундаментальным понятием в теории линейного программирования. Основные результаты теории двойственности заключены в двух теоремах, называемых теоремами двойственности.

ПЕРВАЯ ТЕОРЕМА ДВОЙСТВЕННОСТИ.

Если одна из пары двойственных задач I и II разрешима, то разрешима и другая, причем значения целевых функций на оптимальных планах совпадают, F(x*) = G(y*), где х*, у* - оптимальные решения задач I и II

ВТОРАЯ ТЕОРЕМА ДВОЙСТВЕННОСТИ.

Планы х* и у* оптимальны в задачах I и II тогда и только тогда, когда при подстановке их в систему ограничений задач I и II соответственно хотя бы одно из любой пары сопряженных неравенств обращается в равенство.
Это основная теорема двойственности. Другими словами, если х* и у* - допустимые решения прямой и двойственной задач и если c^Tx*=b^Ty*, то х* и у* – оптимальные решения пары двойственных задач.

ТРЕТЬЯ ТЕОРЕМА ДВОЙСТВЕННОСТИ. Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов b_i системы ограничений - неравенств прямой задачи на величину целевой функции этой задачи:
Δf(x) = b_iy_i

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Значения переменных двойственной задачи y_i, в оптимальном плане называют объективно обусловленными, или двойственными оценками. В прикладных задачах двойственные оценки y_i часто называются скрытыми, теневыми ценами или маргинальными оценками ресурсов.

15. 
    Каково практическое значение теорем двойственности?
    

Практическое значение теорем двойственности состоит в том, что они позволяют заменить процесс решения основной задачи на решение двойственной, которое в определенных случаях может оказаться более простым. Например, задача, область допустимых значений которой описывается двумя уравнениями, связывающими шесть переменных (m = 2, n = 6), не может быть решена графическим методом. Однако данный метод может быть применен для решения двойственной к ней задачи, которая имеет только две переменные.

Практическое значение теорем двойственности состоит в том, что они позволяют заменить процесс решения основной задачи на решение двойственной, которое в определенных случаях может оказаться более простым.

16. 
    Какая из теорем двойственности является критерием оптимальности для задач линейного программирования и в чем ее суть?
    

Первая теорема двойственности. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций совпадают. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

17. 
    Дайте содержательную формулировку и математическую постановку транспортной задачи?
    

Транспортная задача, это специальный вид задачи линейного программирования. Для решения транспортной задачи можно использовать методы решения задач линейного программирования, однако ввиду специфического вида задачи, были построены алгоритмы специально для решения этой задачи. Для решения транспортной задачи в онлайн режиме с подробными пояснениями пользуйтесь калькулятором транспортная задача онлайн.

Общая постановка транспортной задачи заключается в определении оптимального плана перевозок некоторого однородного груза из пунктов отправления A1, A2,..., Am в пункты назначения B1, B2,..., Bn. Критерий оптимальности берется минимальная стоимость перевозки или минимальное время доставки груза.

Рассмотрим транспортную задачу, где в качестве критерия оптимальности взята минимальная стоимость перевозок всего груза. Обозначим через Сij тарифы перевозки единицы груза из пункта отправления i в пункт назначения j. Обозначим через Ai запасы груза i-м пункте отправления, а через Bj потребности груза j-м пункте назначения, а через Xj количество единиц груза переводимого из пункта отправления i в пункт назначения j.

Тогда математическая модель транспортной задачи состоит в определении минимального значения функции

18. 
    Что такое условие баланса и какова его роль в транспортных задачах?
    

Это условие для решения закрытых и открытых транспортных задач (ЗТЗ). ешение задачи с неправильным балансом сводится к решению задачи с правильным балансом введением в ее математическую модель фиктивного поставщика или фиктивного потребителя. Тарифы на перевозку грузов от таких поставщиков или к таким потребителям полагаются равными 0 (т.е. фактически соответствующие перевозки не производятся). Транспортная задача с правильным балансом состоит в том, чтобы найти оптимальный план по заданной таблице перевозок, при котором стоимость перевозок будет минимальна. Такая задача актуальна в областях связанных с транспортировкой грузов. 

19. 
    Сформулируйте задачу целочисленного линейного программирования.
    

Под задачей целочисленного линейного программирования (ЦЛП) понимается задача линейного программирования, в которой некоторые (а возможно, и все) переменные должны принимать целые значения. Задача ЦЛП называется полностью целочисленной, если все её переменные должны быть целочисленными. Задачу ЦЛП можно решить, например, как задачу ЛП без учёта условий целочисленности переменных, а затем округлить полученное решение. Использование такого подхода требует проверки допустимости полученного решения. Таким методом часто пользуются при решении практических задач, особенно когда значения переменных настолько велики, что можно пренебречь ошибками округления. Однако при решении задач, в которых целочисленные переменные принимают малые значения, округление может привести к далёкому от истинного оптимума целочисленному решению. Кроме того, при решении задач большой размерности такой метод требует слишком много машинного времени. Например, пусть оптимальное решение соответствующей задачи ЛП имеет вид x1 = 2,4; x2 = 3,5 . Для получения приближённого оптимального решения необходимо рассмотреть четыре точки (2;3); (2;4); (3;3); (3;4) и выбрать среди них допустимую точку с наилучшими значениями целевой функции. Если в задаче имеются 10 целочисленных переменных, то следует рассмотреть 210 = 1024 варианта целочисленного решения. Но даже рассмотрение всех вариантов не гарантирует получения оптимального целочисленного решения задачи.
Одним из методов решения как полностью целочисленных, так и смешанных задач ЦЛП является метод ветвей и границ. Он представляет собой эффективную процедуру перебора всех целочисленных допустимых решений.

20. 
    Сформулируйте задачу о рюкзаке. К какому классу задач целочисленного программирования она относится?
    

Задача о рюкзаке (также задача о ранце) — NP-полная задача комбинаторной оптимизации. Своё название получила от конечной цели: уложить как можно большее число ценных вещей в рюкзак при условии, что вместимость рюкзака ограничена.

В общем виде задачу можно сформулировать так: из заданного множества предметов со свойствами «стоимость» и «вес» требуется отобрать подмножество с максимальной полной стоимостью, соблюдая при этом ограничение на суммарный вес.

Задача о рюкзаке. 1. Классы задач. Класс P — класс задач с полиномиальной сложностью или класс полиномиально-решаемых задач. ... Задачи класса P. Задача называется полиномиальной, т. е. относится к классу P, если существует константа k и алгоритм, решающий эту задачу за время O(nk), где n есть длина входа алгоритма в битах. Это задачи, решаемые за реальное время. Преимущества ... Динамическое программирование обычно применяется к задачам, в которых искомый ответ состоит из частей, каждая из которых в свою очередь дает оптимальное решение некоторой подзадачи.

21. 
    Сформулируйте задачу о коммивояжере. К какому классу задач целочисленного программирования она относится?
    

Сформулированная задача - задача целочисленная. Пусть хij = 1 , если путешественник переезжает из i -ого города в j-ый и хij = 0, если это не так. Формально введем (n+1) город, расположенный там же, где и первый город, т.е. расстояния от (n+1) города до любого другого, отличного от первого, равны расстояниям от первого города. ... Условия задачи: Необходимо посетить 4 города в ходе деловой поездки Спланировать поездку нужно так, чтобы, переезжая из города в город, побывать в каждом не более одного раза и вернуться в исходный город. Определить оптимальный маршрут посещения городов и его минимальное расстояние.

Задача коммивояжёра относится к числу трансвычислительных: уже при относительно небольшом числе городов (66 и более) она не может быть решена методом перебора вариантов никакими теоретически мыслимыми компьютерами за время, меньшее нескольких миллиардов лет. Содержание. 1 История. ... Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Также задача о коммивояжере может быть сведена к задаче целочисленного линейного программирования путем введения в модель дополнительных ограничений.

22. 
    В чем состоит суть задачи раскроя?
    

Задача раскроя — это NP-полная задача оптимизации, по существу, сводимая к задаче о ранце. Задача является задачей целочисленного линейного программирования. Задача возникает во многих областях промышленности. Представим себе, что вы работаете на целлюлозно-бумажном предприятии, и у вас имеется некоторое количество рулонов бумаги фиксированной ширины, но различным заказчикам нужны различные количества рулонов различной ширины. Как разрезать бумагу, чтобы минимизировать отходы?

23. 
    Для каких оптимизационных задач применяется метод динамического программироваия?
    

Динамическое программирование это способ решения сложных задач путём разбиения их на более простые подзадачи. Часто его применяют к целочисленным задачам оптимизации, сводя их к последовательности целочисленных оптимизационных задач меньшей сложности.

При его реализации одновременный выбор значений большого числа переменных решаемой экстремальной задачи заменяется поочередным опре-делением каждой из них в зависимости от возможных обстоя-тельств.

Динамическое программирование придерживается двух подходов к решению задач:

• 
  Нисходящее динамическое программирование, когда исходная задача разбивается на подзадачи. После решения подзадач результаты объединяются для получения решения исходной задачи.
  
• 
  Восходящее динамическое программирование, когда сначала происходит решение подзадач, а затем объединение их результатов для решения общей задачи.
  

24. 
    В чем заключается суть метода динамического программирования?
    

Динамическое программирование – это метод, который позволяет эффективно решать многие задачи, прежде всего, задачи комбинаторной оптимизации. Суть метода в следующем: имеющуюся задачу рекурсивно разбиваем на более маленькие подзадачи, их — на ещё меньшие и так далее.

25. 
    Сформулируйте принцип оптимальности Беллмана.
    

Принцип оптимальности впервые был сформулирован Ричардом Эрнестом Беллманом в 1953 г. (в трактовке Е.С. Вентцель): Каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление таким образом, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Принцип оптимальности Р. Беллмана сформулирован для решения широкого круга задач управления, планирования производственной деятельности, распределения различного рода ресурсов, конструирования, проектирования и др. и вообще для задач принятия решений в многошаговых (многоэтапных) процессах.

Если заданы начальное (точка А) и конечное (точка В) состояния некоторой системы, и переход из начального в конечное состояние осуществляется в несколько промежуточных этапов, на каждом из которых система может находиться в одном из нескольких состояний, и каждому переходу на каждом этапе можно сопоставить некоторые затраты (или прибыль), то задача состоит в том, чтобы выбрать такой путь (то есть все промежуточные состояния), для которого суммарные затраты достигают минимума (или прибыль -максимума). Предположим, что количественная оценка пути это суммарные затраты (сумма затрат по этапам, т.е. сумма шаговых затрат). Пусть на первом этапе из начального состояния (точка А) можно перейти в некоторое конечное число состояний (условно это четыре точки на вертикали 1 рис. 3.5) с соответствующими затратами. Далее, аналогично, из состояний первого этапа (результатов первого шага) можно перейти в конечное число состояний (три точки на вертикали 2) и т.д., вплоть до конечного этапа, на котором из всех возможных состояний возможен переход только в одно конечное состояние (точка В).

26. 
    Дайте понятие идентификации в широком и узком смысле.