Эконометрика. Решение задачи с построением области допустимых решений (одр) и целевой функции для каждой итерации
 Скачать 134.5 Kb. Скачать 134.5 Kb.
|
|
Задача 1 Дать графическое решение задачи с построением области допустимых решений (ОДР) и целевой функции для каждой итерации: Вариант 3. x1 + x2 ≥ 4; 2x1 - x2 ≥ 1; x1 - 2x2 ≥ 1; При естественных ограничениях x1 ≥ 0 и x2 ≥ 0; L (x1, x2) = 2 x1 - 3x2 + 1→ min. Решение Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). Построим уравнение x1+x2 = 4 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 4. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 4. Соединяем точку (0;4) с (4;0) прямой линией. Построим уравнение 2x1-x2 = 1 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = -1. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 0.5. Соединяем точку (0;-1) с (0.5;0) прямой линией. Построим уравнение x1-2x2 = 1 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = -0.5. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 1. Соединяем точку (0;-0.5) с (1;0) прямой линией. 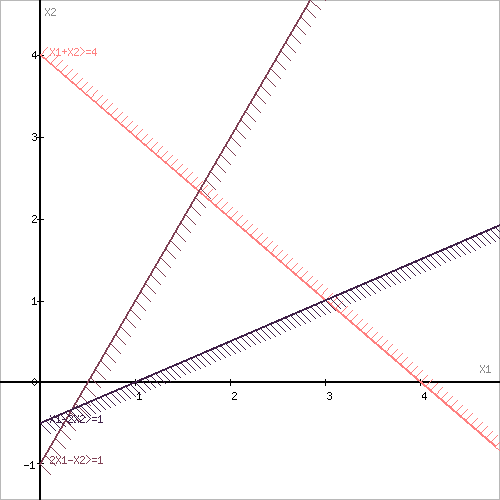 Рис.1. Изображение ограничений в плоскости переменных. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений ( в данном случае он не замкнут).  Рис.2. Границы области допустимых решений (ОДР). Рассмотрим целевую функцию задачи L = 2x1-3x2+1 → min. Построим линию уровня - прямую, отвечающую значению функции L = 0: L = 2x1-3x2+1 = 0 (пунктирная линия на рис.3). Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации L (x1, x2). Начало вектора – точка (0; 0), конец – точка (2; -3). Будем двигать прямую, перпендикулярную этому вектору, параллельным образом в направлении, противоположном направлению градиента – в этом направлении функция наибыстрейшим образом убывает. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до последнего касания ОДР. 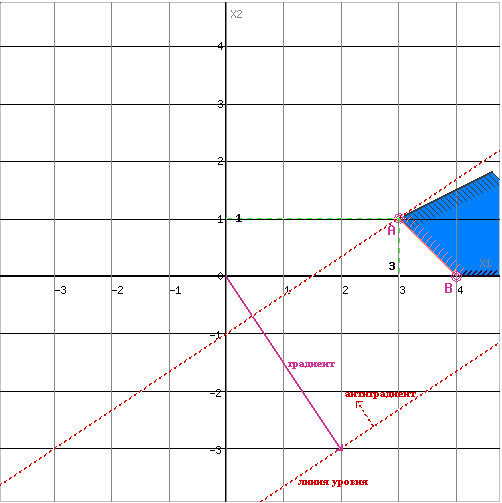 Рис.3. Графическое решение задачи. Прямая L (x1, x2) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых: x1+x2=4 x1-2x2=1 Решив систему уравнений, получим: x1 = 3, x2 = 1. Отсюда найдем минимальное значение целевой функции: L (x1, x2) = 2*3 – 3*1 + 1 = 4 Задача 2. Дать аналитическое решение задачи, переходя к канонической форме (добавлением балансных переменных), расчетом допустимых базисных решений для каждой итерации (провести сопоставление с предыдущим графическим решением на каждом шаге решения задачи): x1 + x2 ≥ 4; 2 x1 - x2 ≥ 1; x1- 2x2 ≥ 1; При естественных ограничениях x1 ≥ 0 и x2 ≥ 0; L (x1, x2) = 2 x1 - 3x2 + 1→ min. Решение Для приведения ЗЛП к канонической форме необходимо ввести неотрицательные балансовые переменные s1, s2, s3. x1 + x2 - s1 = 4; 2 x1 - x2 - s2 = 1; x1 - 2 x2 - s3 = 1; x1, x2, s1, s2, s3 ≥ 0; L (x1, x2) = 2 x1 - 3x2 + 1→ min. Ищем в системе ограничений базисные переменные (входящие только в одно уравнение с единичным коэффициентом). Базисные переменные в исходной задаче отсутствуют, это значит, что исходная задача не содержит в себе допустимого базисного решения. Для его нахождения вначале составим и решим вспомогательную задачу. Введем по одной искусственной неотрицательной переменной ri в каждое уравнение системы ограничений. Получим следующую систему ограничений, x1 + x2 - s1 + r1 = 4 (1) 2 x1 - x2 - s2 + r2 = 1 (2) x1 - 2 x2 - s3 + r3 = 1 (3) x1, x2, s1, s2, s3, r1, r2, r3 ≥ 0 с базисными переменными r1,r2,r3.
Целью решения вспомогательной задачи является получение допустимого базисного решения не содержащего искусственных переменных (r1,r2,r3). Для этого сформируем вспомогательную целевую функцию : G = r1 + r2 + r3 и проведем ее минимизацию в заданной системе ограничений. Если после минимизации функции G ее оптимальное значение будет равно нулю и все искусственные переменные окажутся выведенными из базиса, то полученное базисное решение есть допустимое базисное решение исходной задачи. Если же после минимизации функции G ее оптимальное значение окажется отличным от нуля, значит исходная система ограничений противоречива (область допустимых решений пуста) и исходная задача решения не имеет. Для решения вспомогательной задачи симплекс-методом выразим функцию G через свободные переменные, для этого последовательно вычтем из функции G все уравнения. Функция G примет вид : G = - 4 x1 + 2 x2 + s1 + s2 + s3 + 6. Теперь мы можем сформировать начальную симплекс-таблицу. Начальная симплекс-таблица
В качестве базовой переменной выбираем x1 (у нее в определяющей строке – пока это строка G – максимальный по модулю отрицательный элемент). Разрешающий элемент, стоящий на главной диагонали, РЭ=1. Строка, соответствующая переменной x1, получена в результате деления всех элементов строки x1 на разрешающий элемент РЭ=1. В остальных клетках столбца x1 записываем нули. Все остальные элементы определяются по правилу прямоугольника: выбираются из старого плана четыре числа, расположенные в вершинах прямоугольника и всегда включающие разрешающий элемент РЭ, и новый элемент НЭ находится по формуле НЭ=СЭ-(А*В)/РЭ, где СЭ - элемент старого плана, РЭ - разрешающий элемент, А и В - элементы старого плана, образующие прямоугольник с элементами СЭ и РЭ. Итерация 1
Итерация 2
Итерация 3
Получено оптимальное решение вспомогательной задачи (найден минимум функции G, т.к. в строке целевой функции нет отрицательных коэффициентов). Все искусственные переменные вышли из базиса и поэтому мы можем приступить к решению исходной задачи, приняв полученное базисное решение в качестве опорного. Строка "G" нам больше не нужна, принятие решения о направляющем столбце, во всех последующих итерациях, будем принимать по строке "Q" Итерация 4
Достигнуто оптимальное решение, т.к. в строке целевой функции нет отрицательных коэффициентов. Ответ: Оптимальное значение функции Q(x)= 4 достигается в точке с координатами: x1= 3 и x2= 1 (s1= 0, s2= 4, s3= 0). |
