лабы чм. Лабораторная работа 1 по теме Методы решения нелинейных уравнений
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
Лабораторная работа №1по теме |
| № | Уравнение | 1-й метод | 2-й метод | № | Уравнение | 1-й метод | 2-й метод |
| 1 | x - cos(x / 3) = 0 | 1 | 4 | 16 | sin(1 – 0.2x2) – x = 0 | 3 | 4 |
| 2 | x + ln(4x) – 1 = 0 | 3 | 1 | 17 | ex – e-x – 2 = 0 | 2 | 1 |
| 3 | ex – 4 e-x – 1 = 0 | 2 | 4 | 18 | x – sin(1 / x) = 0 | 4 | 1 |
| 4 | x ex – 2 = 0 | 3 | 2 | 19 | ex + ln(x) – x = 0 | 1 | 2 |
| 5 | 4 (x2 + 1) ln(x) – 1 = 0 | 1 | 3 | 20 | 1–x+sin(x)–ln(1+x) = 0 | 1 | 3 |
| 6 | 2 – x – sin(x / 4) = 0 | 4 | 1 | 21 | (1–x)1/2–cos(1–x) = 0 | 4 | 1 |
| 7 | x2 + ln(x) – 2 = 0 | 1 | 2 | 22 | sin(x2)+cos(x2)–10x = 0 | 3 | 2 |
| 8 | cos(x)–(x + 2)1/2 + 1 = 0 | 2 | 3 | 23 | x2 – ln(1 + x) – 3 = 0 | 2 | 3 |
| 9 | 4 (1 + x1/2) ln(x) – 1 = 0 | 2 | 1 | 24 | cos(x / 2) ln(x – 1) = 0 | 1 | 2 |
| 10 | 5 ln(x) – x1/2 = 0 | 2 | 3 | 25 | cos(x/5) (1+x)1/2–x = 0 | 1 | 3 |
| 11 | ex + x3 – 2 = 0 | 1 | 4 | 26 | 3x – e-x = 0 | 4 | 2 |
| 12 | 3 sin (x1/2) + x – 3 = 0 | 3 | 1 | 27 | 4(1+x1/2) ln(x)–10 = 0 | 1 | 3 |
| 13 | 0.1x2 – x ln(x) = 0 | 1 | 4 | 28 | sin(x)–31/2cos(x)+4x–4 = 0 | 3 | 4 |
| 14 | cos(1 + 0.2x2) – x = 0 | 1 | 3 | 29 | x – 1 / (3 + sin(3.6x)) = 0 | 1 | 3 |
| 15 | 3 x – 4 ln(x) – 5 = 0 | 1 | 2 | 30 | 0.25x3 + cos(x / 4) = 0 | 4 | 2 |
В табл. 1-1 номера методов: 1 – половинное деление;2 – итерации;3 – Ньютона; 4 – хорд.
1.4. Содержание отчета
Индивидуальное задание (уравнение, методы для выполнения 3-х итераций).
Результат отделения корней (график функции, таблица значений функции и её производных, вывод об отделённом отрезке, содержащем один корень).
Результаты исследования функции уравнения для проведения расчетов. Привести для каждого метода:
условие сходимости вычислительного процесса;
начальное приближение;
условие окончания этапа уточнения корня.
В сценарии мат. пакета создать функции для проведения расчета 1-м методом. Результаты расчета по каждому методу свести в табл. 1-2.
Таблица 1-2
| к | x | f(x) |
| 1 | | |
| 2 | | |
| 3 | | |
| 4 | | |
Оценки погрешностей результатов расчетов после 3-х итераций с использованием формулы, соответствующего метода.
Создать программу для решения уравнения 2-м заданный методом с точностью
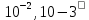 10-4. Построить график зависимости количества итераций от точности в логарифмическом масштабе.Решение нелинейного уравнения с использованием функции fsolve.
10-4. Построить график зависимости количества итераций от точности в логарифмическом масштабе.Решение нелинейного уравнения с использованием функции fsolve.1.5. Пример выполнения задания с использованием мат. пакета MathCad
Решить уравнение
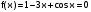 ;
;методы решения нелинейных уравнений – половинного деления, итерации, Ньютона и хорд;
Этап отделения корней.
Используем для этого математический пакет MathCad. Отделение корней произведем как графическим методом (график функции), так и аналитически (таблица).
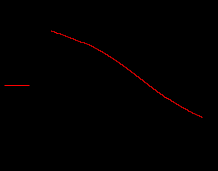     |
Рис.1. Графическое и аналитическое отделение корней уравнения.
Из построенного графика функции f(x) видно, что на отрезке (0, 1) есть один корень. На этом графический способ отделения корней заканчивается.
Другой вариант отделения корня – решить задачу аналитически.
Для аналитического отделения корня построена таблица рис.1. Она требует пояснений. В столбцах таблицы выведены некоторые значения аргумента x на заданном отрезке, а также значения функций f(x),
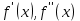 при этих значениях x.
при этих значениях x. Видно, что на отрезке (0, 1) функция f(x) меняет знак, значит существует, по крайней мере, один корень.
Значения первой производной
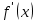 в заданных точках отрезка (0, 1) не меняет знак, что вызывает некоторую надежду о том, что
в заданных точках отрезка (0, 1) не меняет знак, что вызывает некоторую надежду о том, что 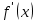 не меняет знак на всем отрезке (0, 1), но делать вывод об этом не совсем корректно с точки зрения математики. Однако анализ аналитического выражения
не меняет знак на всем отрезке (0, 1), но делать вывод об этом не совсем корректно с точки зрения математики. Однако анализ аналитического выражения 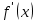 = –sin(x)–3 приводит к выводу, что
= –sin(x)–3 приводит к выводу, что 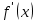 <= -2 при любых значениях x. А это значит, что
<= -2 при любых значениях x. А это значит, что 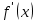 отрицательно на всем отрезке (0, 1), и уже из этого следует, что на отрезке (0, 1) функция f(x) монотонна и имеет один корень.
отрицательно на всем отрезке (0, 1), и уже из этого следует, что на отрезке (0, 1) функция f(x) монотонна и имеет один корень.Значения первой и второй производной
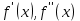 на отрезке (0, 1) из таблицы рис.1 будут использованы в методах Ньютона, хорд и итераций.
на отрезке (0, 1) из таблицы рис.1 будут использованы в методах Ньютона, хорд и итераций.Этап уточнения корня
Метод половинного деления
Исследование задания
Метод половинного деления сходится, если на выбранном отрезке отделен один корень. Так как на отрезке [0;1] функция
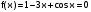 меняет знак (
меняет знак (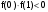 ) и монотонна (f′(x)<0), то условие сходимости выполняется.
) и монотонна (f′(x)<0), то условие сходимости выполняется. Выберем за начальное приближение середину отрезка
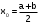 =0.5.
=0.5.Условие окончания процесса уточнения корня. Для оценки погрешности метода половинного деления справедливо условие
|bn – an|<ε , т.е. длина отрезка, полученного на n-ом шаге должна быть меньше заданной точности -
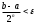
Результаты «ручного расчета» трех итераций
| 1 итерация 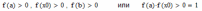 следовательно, 2 итерация 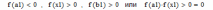 следовательно, 3 итерация 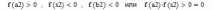 следовательно, и т.д. |
Рис.2. Три итерации метода половинного деления
Результаты вычислений представлены в форме табл. 1-2а.
| n | an | bn | f(an) | f(bn) | (an+bn)/2 | f( (an+bn)/2) | bn-an |
| 0 | 0 | 1 | 2 | -1.459 | 0.5 | 0.377 | 1 |
| 1 | 0.5 | 1 | 0.377 | -1.459 | 0.75 | -0.518 | 0.5 |
| 2 | 0.5 | 0.75 | 0.377 | -0.518 | 0.625 | -0.064 | 0.25 |
| 3 | 0.5 | 0.625 | | | | | 0.125 |
После трех итераций приближение к корню – середина отрезка [a3, b3] – x3=0.5625.
Оценка погрешности результата после трех итераций: R = | b3 – a3 | = 0.125.
Это значит, что x3 отличается от неизвестного точного значения корня не больше чем на величину R = 0.125.
Метод простых итераций
1) Исследование задания
Приведем уравнение f(x)=0 к виду
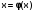 . Тогда рекуррентная формула
. Тогда рекуррентная формула 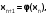
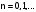 . Для сходимости процесса простых итерации необходимо, чтобы
. Для сходимости процесса простых итерации необходимо, чтобы 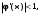 при
при 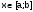 . Если
. Если 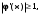 то сходимость не обеспечена.
то сходимость не обеспечена. Приведем уравнение
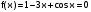 к виду x = (cos(x)+1)/3 и проведем исследование.
к виду x = (cos(x)+1)/3 и проведем исследование. 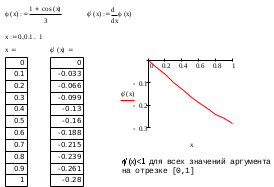 |
В приведенном примере условие сходимости выполняется и можно использовать итерирующую/итерационную функцию
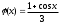 в рекуррентной формуле для уточнения корня методом итераций, что и будет показано ниже. Однако, в случаях, когда свободный х выразить не удается, или когда
в рекуррентной формуле для уточнения корня методом итераций, что и будет показано ниже. Однако, в случаях, когда свободный х выразить не удается, или когда Построим функцию j(x) = х + lf(x), где параметр
 может быть определен по правилу: l =
может быть определен по правилу: l = 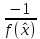 , а в знаменатель следует подставить
, а в знаменатель следует подставить 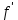 (x), у которого
(x), у которого 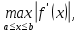 то есть
то есть l =
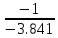
Тогда рекуррентная формула: φ(x)= x + (1 - 3x + cos x)/3.841.
2) «Ручной расчет» трех итераций
Для получения решения уравнения методом итерации необходимо воспользоваться следующей рекуррентной формулой:
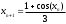 ,
,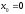
| |
Результаты вычислений представлены в форме табл. 1-2б.
| к | Xк | f(xк) |
| 0 | 0 | 2 |
| 1 | 0.667 | -0.214 |
| 2 | 0.595 | 0.042 |
| 3 | 0.609 | -7.95 • 10-3 |
Сходимость итерационного процесса подтверждается принадлежностью всех
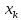 выбранному исходному отрезку изоляции корня [0;1] и стремлением f(
выбранному исходному отрезку изоляции корня [0;1] и стремлением f(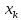 ) к нулю.
) к нулю.Получим оценку погрешности результата после трех итераций:
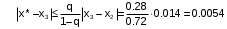
Метод хорд
1) Исследование задания.
Необходимые и достаточные условия сходимости аналогичны методу Ньютона, а именно:
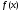 непрерывна на [a;b] и
непрерывна на [a;b] и 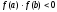 ;
; 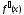 и
и 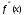 отличны от нуля и сохраняют знаки для
отличны от нуля и сохраняют знаки для 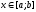 .
.В нашем случае на отрезке [0;1] требования сходимости выполняются.
На этапе отделения корня было показано, что для функции f(x)=1–3x+cosx вторая производная
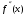 <0 на отрезке [0;1] и, следовательно, неподвижной точкой является точка
<0 на отрезке [0;1] и, следовательно, неподвижной точкой является точка 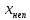 = b = 1, так как
= b = 1, так как 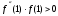 .
.Таким образом, полагая
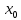 = a= 0, получим сходящуюся последовательность приближений к корню.
= a= 0, получим сходящуюся последовательность приближений к корню.В рассматриваемой задаче рекуррентная формула принимает следующий вид
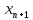 =
= 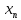 +
+ 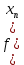
Оценку погрешности можно проводить по любой из формул
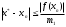 или
или 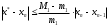 , где m1 и M1 – наименьшее и наибольшее значения
, где m1 и M1 – наименьшее и наибольшее значения 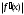 на отрезке. В случае, если M1
на отрезке. В случае, если M12) Расчет трех итераций
Для получения решения уравнения методом хорд воспользуемся следующей рекуррентной формулой:
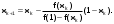
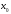 = 0.
= 0.    |
Результаты вычислений представлены в виде следующей таблицы:
| n | Xn | f(xn) |
| 0 | 0 | 2 |
| 1 | 0.5781 | 0.10325 |
| 2 | 0.6059 | 4.0808 •10-3 |
| 3 | 0.60706 | 1.59047•10-4 |
3) Оценку погрешности результата, вычисленного методом хорд, получим по формуле
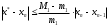 . Тогда после трех итераций
. Тогда после трех итераций |
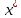 -
-  | <=
| <= 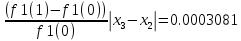
Метод Ньютона
1) Исследование задания.
Необходимые и достаточные условия сходимости метода Ньютона:
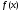 непрерывна на [a;b] и
непрерывна на [a;b] и 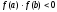 ;
; 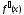 и
и 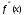 отличны от нуля и сохраняют знаки для
отличны от нуля и сохраняют знаки для 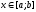 .
.В нашем случае на отрезке [0;1] требования сходимости выполняются.
Начальное приближение
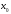 должно удовлетворять условию:
должно удовлетворять условию: 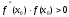 , т.е. за начальное приближение следует принять тот конец отрезка, где знак функции и знак второй производной совпадают. Поскольку
, т.е. за начальное приближение следует принять тот конец отрезка, где знак функции и знак второй производной совпадают. Поскольку 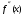 < 0 и
< 0 и 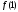 < 0, то выберем начальное приближение к корню:
< 0, то выберем начальное приближение к корню: 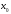 =1.
=1.2) Расчет трех итераций
Для получения решения уравнения методом Ньютона воспользуемся следующей рекуррентной формулой:
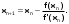
В нашем случае
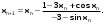 ,
, 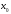 =1.
=1.| |
Представим вычисления в виде следующей табл. 1-2б.
| k | Xk | f(xk) |
| 0 | 1 | -1.4597 |
| 1 | 0.62 | -0.046 |
| 2 | 0.607121 | -6. 788 •10-5 |
| 3 | 0.60710164814 | -1.484 •10-10 |
Оценим погрешность после трех итераций:
Сравните оценки погрешности методов после трех итераций. Представляется, что комментарии излишни.
