лабы чм. Лабораторная работа 1 по теме Методы решения нелинейных уравнений

• Название: Лабораторная работа 1 по теме Методы решения нелинейных уравнений
• Анкор: лабы чм
• Дата: 12.05.2023
• Размер: 0.5 Mb.
• Имя файла: NLU_Interp_MNK_Integr_ODU_LAB_12883677.docx
• Тип: Лабораторная работа; #1124506
• страница: 2 из 7

Контрольные вопросы  по теме

«Методы решения нелинейных уравнений»

 

1.      Что является корнем нелинейного уравнения f(x)=0?

2.      Чему равна функция в точке корня?

3.      Каково условие существования на отрезке [a;b] хотя бы одного корня?

4.      При каких условиях корень x будет единственным  на отрезке [a;b]?

5.      Из каких этапов состоит процесс решения нелинейного уравнения? 

6.     В чем заключается этап «отделения корней» нелинейного уравнения?

7.  Какие методы используются на этапе отделения корней?

8. Что необходимо, чтобы выбрать x0 в качестве начального приближения в методе

Ньютона?

9. Какой метод решения нелинейного уравнения требует  более близкого к корню

начального значения?

10.  Какой метод представляет собой метод решения нелинейного уравнения, в результате которого получается последовательность вложенных отрезков?

11.  Можно ли уточнить корень уравнения графическим методом?

12. Что является  первым приближением к корню, отделенному на отрезке [a;b],  при

решении нелинейного уравнения методом половинного деления?

13.  Каково правило выбора итерирующей функции при использовании метода итераций?

14.  Что принимается за начальное приближение в методе итерации?

15.  Каково правило выбора неподвижной точки при использовании метода хорд?

16.  Какое значение выбирается в качестве начального приближения в методе хорд?

17.  Для каких функций не рекомендуется применять метод Ньютона?

18. Можно ли применять метод итераций, если на заданном отрезке имеются два корня?

19.  Какой метод решения нелинейного уравнения обладает свойством «самокоррекции»?

20.  Что относится к способам улучшения сходимости метода простой итерации?

Лабораторная работа №2

по теме «Интерполяция функций»

1. Вопросы, подлежащие изучению

1. 
   Постановка задачи аппроксимации и интерполяции. Интерполяция в точке. Погрешность интерполяции.
   
2. 
   Основные понятия: интерполирующая и интерполируемая функции, условие интерполяции. Связь между числом узлов интерполяции и порядком интерполирующего полинома.
   
3. 
   Интерполяционный полином Лагранжа: назначение, область применения.
   
4. 
   Интерполяционная формула Ньютона, область применения.
   
5. 
   Конечные разности, их назначение и использование. Свойства конечных разностей
   
6. 
   Методика выбора узлов интерполяции при использовании формул Лагранжа и Ньютона.
   
7. 
   Способы оценки погрешностей интерполяции по формулам Лагранжа и Ньютона. Способы повышения точности интерполяции.
   

2. 
   Задание
   

В этой лабораторной работе решается задача интерполяции в точке путем построения семейства интерполяционных полиномов разных степеней с оценкой погрешности полученных решений.

1. 
   Выбрать из таблицы 1–1 индивидуальное задание для интерполяции:
   

• 
  точку интерполяции x=b для интерполяции полиномом Лагранжа;
  
• 
  точку интерполяции x=a для интерполяции полиномом Ньютона;
  

2. 
   Выполнить вручную интерполяцию в заданной точке x=b с использованием полинома Лагранжа 1–й, 2–й b3–й степени:
   

• 
  выбрать из таблицы 2–2 с интерполируемой функцией четыре подходящих узла. Перенумеровать узлы и занести перенумерованные узлы в таблицы вида 1–3.
  
• 
  записать интерполяционные формулы для 1, 2 и 3-ей степени полинома;
  
• 
  выполнить расчеты по интерполяционным формулам для каждой степени полинома; все промежуточные вычисления производить с сохранением всех значащих цифр, окончательные результаты округлять до 4 знаков после десятичной точки.
  
• 
  занести полученные результаты в таблицу вида 1–4;
  
• 
  вычислить оценки погрешности в точке b для полиномов различных степеней и занести их в таблицу 1-4.
  

1. 
   Выполнить вручную интерполяцию в заданной точке x=a с использованием полинома Ньютона 1–й, 2–й и 3–й степени:
   

• 
  выбрать из таблицы 1–2 с интерполируемой функцией четыре подходящих узла. Перенумеровать узлы и занести перенумерованные узлы в таблицы вида 1–3.
  
• 
  заполнить таблицу конечных разностей (для интерполяционной формулы Ньютона);
  
• 
  записать интерполяционные формулы для 1, 2 и 3-ей степени полинома;
  
• 
  выполнить расчеты по интерполяционным формулам для каждой степени полинома; все промежуточные вычисления производить с сохранением всех значащих цифр, окончательные результаты округлять до 4 знаков после десятичной точки.
  
• 
  занести полученные результаты в таблицу вида 1–5;
  
• 
  вычислить оценки погрешности в точке а для полиномов различных степеней и занести их в таблицу 1-5.
  

4. 
   Объяснить полученные результаты и сделать выводы.
   

1.3. Варианты задания для ручного расчета и таблица интерполируемой функции

Таблица 1–1

№ варианта	Полином Ньютона x=a	Полином Лагранжа x=b
1	0.06	0.43
2	0.11	0.72
3	0.16	1.17
4	0.21	0.58
5	0.31	0.12
6	0.36	1.21
7	0.41	1.46
8	0.46	0.87
9	0.51	0.48
10	0.61	1.37
11	0.07	0.51
12	0.12	0.96
13	0.17	0.64
14	0.22	1.52
15	0.32	0.77
16	0.37	0.17
17	0.42	1.02
18	0.52	0.34
19	0.62	1.41
20	0.08	0.23
21	0.13	0.67
22	0.17	1.29
23	0.23	0.81
24	0.32	1.26
25	0.42	1.12
26	0.47	0.93
27	0.53	0.37
28	0.63	0.26
29	0.09	1.07
30	0.14	1.33

Таблица 1–2

№ узла	Значение аргумента xi	Значение функцииyi
0	0.05	-4.1710
1	0.10	-4.1330
2	0.15	-4.0845
3	0.20	-4.0240
4	0.25	-3.9500
5	0.30	-3.8610
6	0.35	-3.7555
7	0.40	-3.6320
8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385
11	0.60	-2.9280
12	0.65	-2.6920
13	0.70	-2.4290
14	0.75	-2.1375
15	0.80	-1.8160
16	0.85	-1.4630
17	0.90	-1.0770
18	0.95	-0.6565
19	1.00	-0.2000
20	1.05	0.2940
21	1.10	0.8270
22	1.15	1.4005
23	1.20	2.0160
24	1.25	2.6750
25	1.30	3.3790
26	1.35	4.1295
27	1.40	4.9280
28	1.45	5.7760
29	1.50	6.6750
30	1.55	7.6265

1.4. Формы таблиц для занесения результатов

Таблица 1–3

k	0	1	2	…	n
xk	x0	x1	x2	…	xn
yk	y0	y1	y2	…	yn

Таблица 1-4

(для полинома Лагранжа)

Степень многочлена k	Lk(x)	Погрешность
1	L1(x)	|L1(x) – L2(x)|
2	L2(x)	|L2(x) – L3(x)|
3	L3(x)	–

Таблица 1–5

(для полинома Ньютона)

Степень многочлена k	Pk(x)	Погрешность
1	P1(x)	|P1(x) – P2(x)|
2	P2(x)	|P2(x) – P3(x)|
3	P3(x)	–

1.5. Содержание отчета

1. Фамилия и имя студента, номер группы.

2. Название и цель лабораторной работы.

3. Индивидуальный вариант задания к работе.

4. Таблицы 1–3 с перенумерованными узлами интерполяции.

5. Интерполяционные формулы для ручных расчетов и результаты расчетов в таблицах 1–4 и 1-5.

6. Выводы.

1.6. Пример выполнения задания

1. 
   Точка интерполяции для формулы Лагранжа b = 0.52.
   

Выбор и перенумерация узлов.

Для ручной интерполяции в точке x = b = 0.52 по формуле Лагранжа выбираем из таблицы 3–2 4 узла так, чтобы точка b = 0.52 оказалась внутри получающийся таблицы и узлы были наиболее близкими к этой точке. В итоге выбираем узлы с номерами 8, 9, 10, 11:

8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385
11	0.60	-2.9280

Следует отметить, что формула Лагранжа может использоваться как для таблиц с постоянным шагом, так и с непостоянным шагом. Перенумеруем узлы интерполяции руководствуясь двумя правилами: точка x=b должна быть внутри таблицы и узлы должны быть ближайшие к ней. Занесем перенумерованные узлы в таблицу вида 2–3:

k	0	1	2	3
xk	0.50	0.55	0.45	0.60
yk	-3.3250	-3.1385	-3.4890	-2.9280

Ручной расчет по формуле Лагранжа.

Запишем интерполяционные полиномы Лагранжа 1–й, 2–й и 3–й степени и вычислим их значения в точке x = b = 0.52: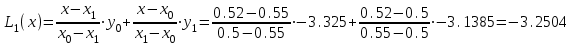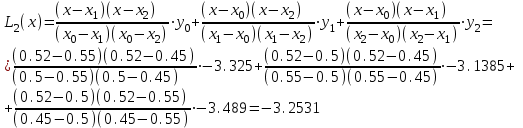





Обратите внимание, что: выражения для полиномов 1, 2 и 3 степени (в явном виде) после соответствующих преобразований следует получить самостоятельно!

Занесем результаты в таблицу и вычислим оценки погрешности полученных значений для многочленов 1–й и 2–й степени:

Степень многочлена k	Lk(x)	Оценка погрешности
1	–3.2504	0.0027
2	–3.2531	0.0001
3	–3.2532	–

Вывод. Получены выражения для интерполяционных полиномов 1, 2 и 3-ей степени и их значения в т. b. Оценку погрешности проведём в соответствии с неравенством:


Можно утверждать, что разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.52 после 3=х итераций не превышает 0.0001.

1. 
   Точка интерполяции для формулы Ньютона a = 0.12.
   

Выбор и нумерация узлов.

Для ручной интерполяции в точке x = a = 0.12 по 1 формуле Ньютона выбираем 4 узла из таблицы 1–2 так, чтобы точка a = 0.12 оказалась между узлами с номерами с 1 по 2 и добавляем узлы вправо:

Номера выбранных узлов (k)	xk	yk
1	0.10	-4.1330
2	0.15	-4.0845
3	0.20	-4.0240
4	0.25	-3.9500

Выбор точек определяется тем, чтобы при решении задачи интерполяции в точке по первой формуле Ньютона, точка должна быть внутри таблицы для полинома любой степени, в том числе и первой. Поэтому нулевой и первый узел должны находиться по разные стороны от самой точки x=a. Если нулевой узел находится слева от точки, а первый узел находится справа от точки, то шаг h=x1-x0 будетположительным и добавлять узлы следует справа относительно точки x=a. Если же нулевой узел находиться справа от точки, а первый узел находиться слева, то шаг h=x1-x0 будет отрицательным, и добавлять узлы следует слева.

Изменим нумерацию узлом интерполяции для использования их в интерполяционных формулах и занесем в таблицы вида 1–3.

k	0	1	2	3
xk	0.10	0.15	0.20	0.25
yk	-4.1330	-4.0845	-4.0240	-3.9500

Ручной расчет по формуле Ньютона.
Заполним таблицу конечных разностей:

x	y	Δy	Δ2y	Δ3y
0.10	-4.1330	0.0485	0.0120	0.0015
0.15	-4.0845	0.0605	0.0135
0.20	-4.0240	0.0740
0.25	-3.9500

Запишем 1–ю интерполяционную формулу Ньютона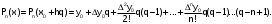



для полиномов 1–й, 2–й и 3–й степени и выполним расчеты по ним. Определим значение q: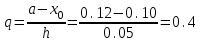



Значение полинома 1-й степени в т. x=0.12: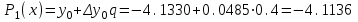


Значение полинома 2-й степени в т. x=0.12: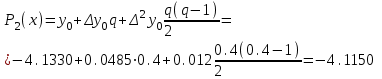



Значение полинома 3-й степени в т. x=0.12:
Важно: Явные выражения для полиномов 1, 2 и 3 степени могут быть получены после соответствующих преобразований формулы: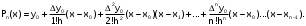


В нашем случае они будут иметь вид: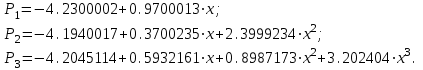


Занесем результаты в таблицу и вычислим оценки погрешности полученных значений для полиномов 1–й и 2–й степени:

Степень многочлена k	Pk(x)	Оценка погрешности
1	–4.1136	0.0014
2	–4.1150	0.0001
3	–4.1149	–

Вывод. Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в точке а. Оценку погрешности проведём в соответствии с неравенством:



Можно утверждать, что разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.12 после 3-х итераций не превышает 0.0001.

Контрольные вопросы по теме

«Интерполяция функций»

1. 
   Что называется задачей интерполяции и задачей аппроксимации?
   
2. 
   Что называется узлами и шагом интерполяции?
   
3. 
   Что такое интерполируемая функция и интерполирующая функция?
   
4. 
   Существует ли связь между числом узлов интерполяции и степенью интерполяционного многочлена?
   
5. 
   Можно ли, используя одни и те же узлы интерполяции, построить несколько интерполяционных полиномов?
   
6. 
   Сколько интерполяционных полиномов степени n существует, если функция задана (n + 1) узлом?
   
7. 
   Изменится ли точность интерполяции при увеличении или уменьшении количества узлов?
   
8. 
   Как изменится формула Лагранжа при добавлении в таблицу значений функции еще одного узла?
   
9. 
   Как изменится формула Ньютона при добавлении в таблицу значений функции еще одного узла?
   
10. 
    Если интерполируемая функция f(x)задана в (n + 1) равноотстоящих узлах, то для ее интерполяции удобнее использовать формулу Ньютона или формулу Лагранжа?
    
11. 
    Можно ли при использовании формулы Лагранжа располагать узлы интерполяции в произвольном порядке?
    
12. 
    Можно ли при использовании формулы Ньютона располагать узлы интерполяции в произвольном порядке?
    
13. 
    Потребуется ли полный пересчет коэффициентов формулы Лагранжа при добавлении дополнительного узла интерполяции?
    
14. 
    В чем заключается универсальность формулы Лагранжа?
    
15. 
    От чего зависит точность интерполяции?
    
16. 
    Что такое «конечные разности»?
    
17. 
    Чему равен порядок конечной разности наивысшего порядка, полученный по n исходным точкам?
    
18. 
    Что происходит с формулой Ньютона при добавлении очередного узла интерполяции?
    
19. 
    Чем отличаются результаты интерполяции, если при построении интерполяционных полиномов по формулам Лагранжа и Ньютона были использованы одни и те же узлы?
    
20. 
    Чему равна степень интерполяционного полинома Ньютона при трех заданных точках интерполируемой функции?