Артем№1. Математическая модель. Пусть x1, x2 количество декалитров пива и эля соответственно
 Скачать 33 Kb. Скачать 33 Kb.
|
|
№1. Математическая модель. Пусть x1, x2 – количество декалитров пива и эля соответственно. Найти наибольшее значение функции F = 5x1 + 2x2 при следующих ограничениях: 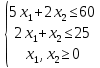 Рассмотрим неравенство 1 системы ограничений. 5 x1 + 2 x2 ≤ 60 Построим прямую: 5 x1 + 2 x2 = 60 Пусть x1 =0 => 2 x2 = 60 => x2 = 30 Пусть x2 =0 => 5 x1 = 60 => x1 = 12 Найдены координаты двух точек (0, 30) и (12 ,0). Соединяем их и получаем необходимую прямую (1). Рассмотрим неравенство 2 системы ограничений. 2 x1 + x2 ≤ 25 Построим прямую: 2 x1 + x2 = 25 Пусть x1 =0 => x2 = 25 Пусть x2 =0 => 2 x1 = 25 => x1 = 25/2 Найдены координаты двух точек (0, 25) и (25/2 ,0). Соединяем их и получаем необходимую прямую (2). Строим область допустимых решений: 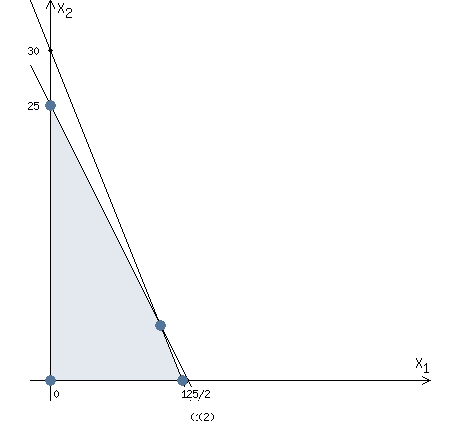 Строим вектор C = (5, 2), координатами которого являются коэффициенты функции F. Функция достигает максимума в точках А и В одновременно. 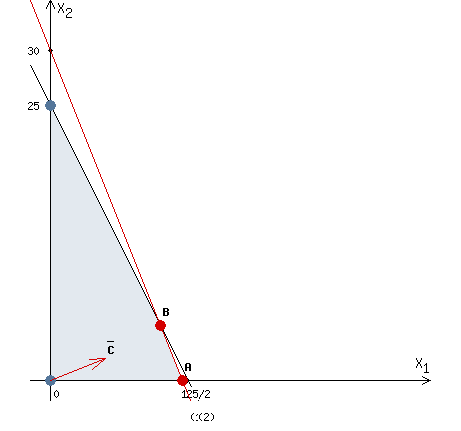 Координаты точки A (12,0). F_max = 5 * 12 + 2 * 0 = 60. Точка B одновременно принадлежит прямым (1) и (2). 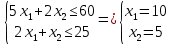 Вычислим значение функции F в точке B (10,5). F_max = 5 * 10 + 2 * 5 = 60. Вывод: Для получения максимальной прибыли в размере 60$ необходимо произвести 12 декалитров пива или 10 декалитров пива и 5 декалитров эля. |
