Отчет 2.2. Математическая модель сообщества производители продукт управленцы
 Скачать 438.11 Kb. Скачать 438.11 Kb.
|
|
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СООБЩЕСТВА «ПРОИЗВОДИТЕЛИ – ПРОДУКТ – УПРАВЛЕНЦЫ» Дана следующая математическая модель:  У которой a, b, l, ε1, ε2, δ, h, k, g, e, d, c, f, x(t), y(t), z(t) > 0 Где количество x – управленцев, y – количество производителей, z – количество продукта. Для данной задачи я выбрал численный метод предиктор-корректор второго порядка. Но численный метод начинает адекватно работать только начиная с разбиения N = 163840. Начальными условиями я взял x0 = 0.15, y0 = 0.1, z0 = 10. Отрезок времени t ⋲ [0, 15000]. Причины, по которым я взял такой отрезок заключается в том, что это примерно оптимальный отрезок, на котором мы можем увидеть стационарный поведение функций x(t), y(t), z(t). Далее мы определим, правда ли достигаются стационарные состояния, по формулам, предложенным в книге Неймарк Ю.И., а так же поймем, как ведут себя функции, при варьировании констант модели. 2 варианта формул, для определения стационарных значений функций.  При варьировании констант, мы заметим, что будет выполняться одна из предложенных формул. Далее, так как выкладывать все варьирования (по 3 на каждый из 15 параметров), мы рассмотрим только некоторые случаи. Во всех графиках будет сразу три вариации, одного параметра. 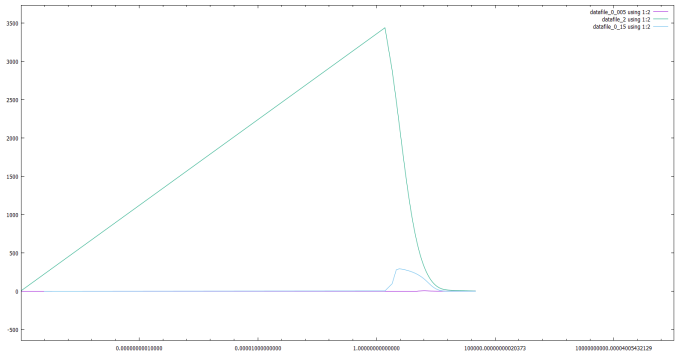   Первый x, второй z, третий y, от t В данном случаем, мы варьировали параметр а, как мы можем заметить здесь выполняется первая формула для стационарных точек. Так же можем заметить, что a влияет на высоту горба функций. Так же заметим, что при небольшом росте а количество управленцев резко возрастает, а так же почти в то же мгновение начинает резко падать. В случае с продуктом там все, можно сказать стабильно, а вот производителей, чем больше a, тем их меньше. Так же для данного случая можно увидеть зависимости каждой функции от друг друга.   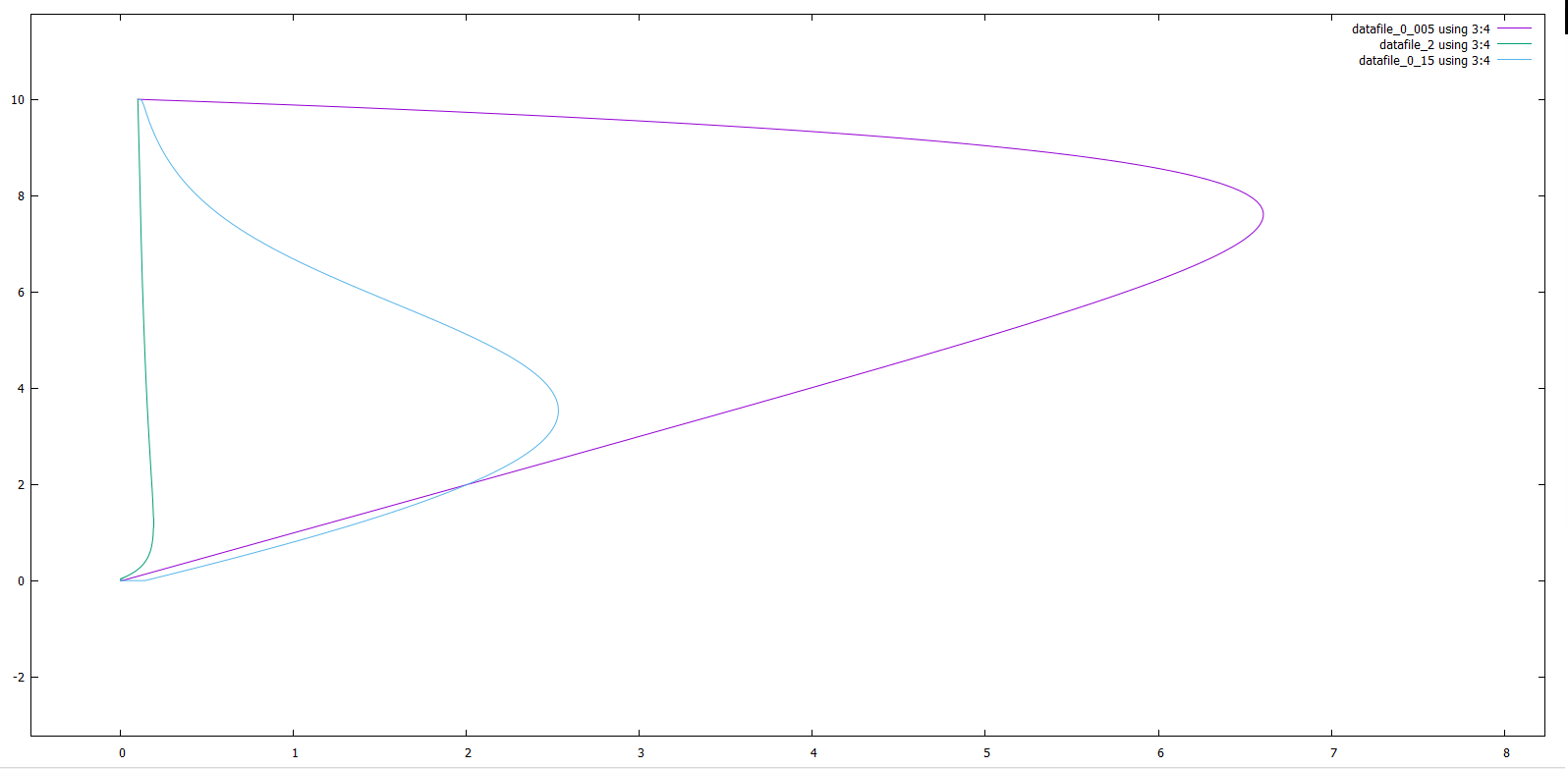 Первый это y от x, второй z от x, третий z от y Как мы и говорили. При увеличении управленцев резко падает количество производителей (напоминает 90-е, когда все хотели стать управленцами или во время дефолта, когда был резкий скачок увеличения количества богачей, а потом дефолт и все стали банкротами). Так же при увеличении а, замечаем, что при увеличении управленцев, скорость убывания товара резко уменьшается. Рассмотрим теперь случай, когда так же у нас себя ведут производители. В данном случае варьируем параметр f .   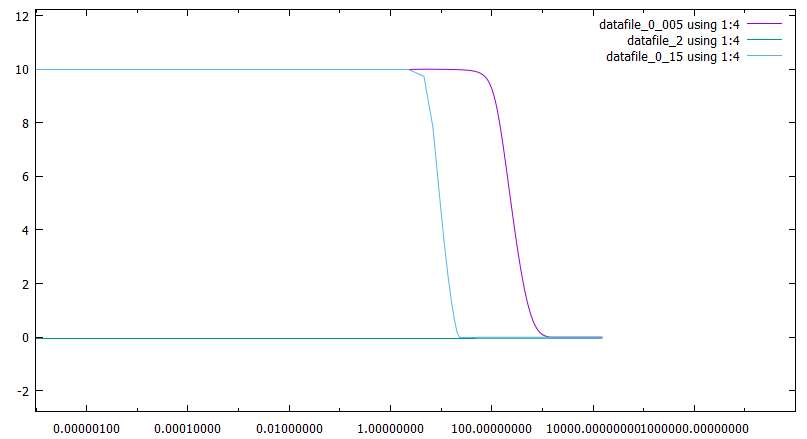 Заметим, что в данном случае у нас происходит резкий рост производителей и увеличение скорости падения количества товаров, что достаточно странно. Так как следуя обычной логике, чем больше производителей, тем больше производство. Возможно, дело заключается в том, что количество управленцев тоже уменьшается. То есть, так как начальства мало, а рабочих много, они халтурят и в итоге производство катит в лету. Так же можно увидеть это, понаблюдав за зависимостью x,y,z друг от друга.   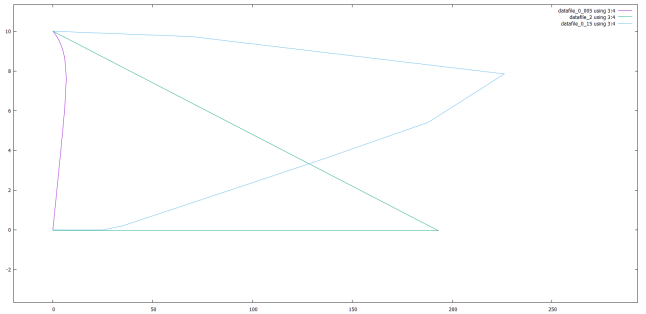 Все что мы обговорили ранее, мы можем заметить на этих зависимостях. В данном случае, тоже выполняется первая формула для стационарных точек. Далее рассмотрим случай, когда у нас идет хороший рост продуктов, а затем и рост производителей. Здесь мы будем варьировать параметр g. Он отвечает за технологический уровень, чем больше, тем производство лучше.  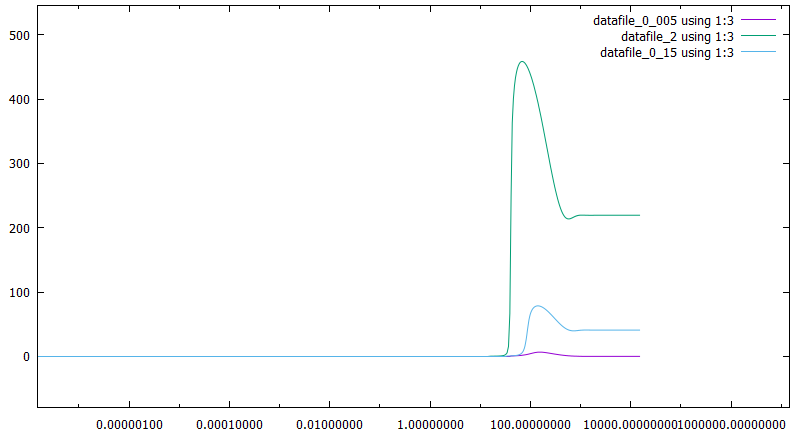 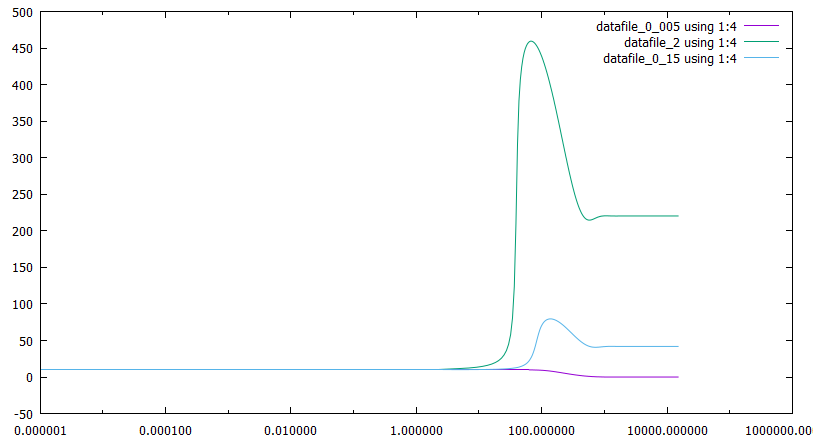 Этот случай особенен тем, что в данном случае мы получаем стационарные точки не нулевые и в случае для функции y оно не совпадает с формулой из Неймарка. Так же здесь можно заметить стабильное экономическое состояние. Нет большого количества управленцев, стабильный штат производителей и постоянное количество продукта, нет не излишков, и нет недостатка. Из всех выше пересмотренных случаев, я считаю, что, даже не варьируя остальные параметры, это разумный набор параметров. Рассмотрим зависимости x, y, z друг от друга, а так же посмотрим на погрешность по Рунге и посмотрим некоторые оптимальные h для некоторых процентных соотношений.    Рассмотрим погрешность по Рунге. Рассмотрим ее при g = 0.005
Так же рассмотрим некоторые h их процентное соотношение.
Вот мы все сделали, сделали анализ, но самого главного мы не сделали, мы не показали, что наш метод сходится, сейчас это и сделаем, на следующих 3-х графиках, мы увидим, что при уменьшении h функции сходятся к одной. 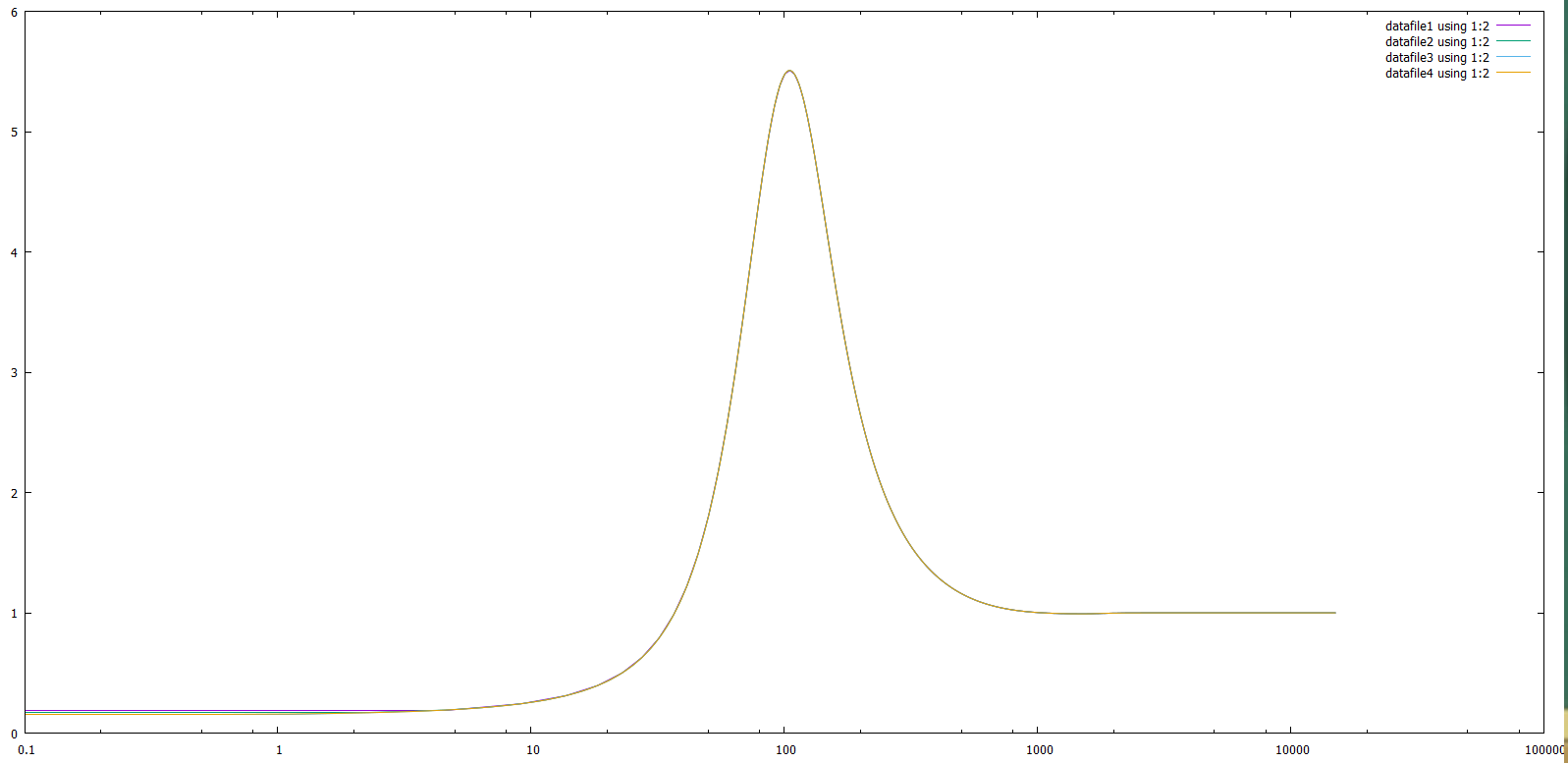 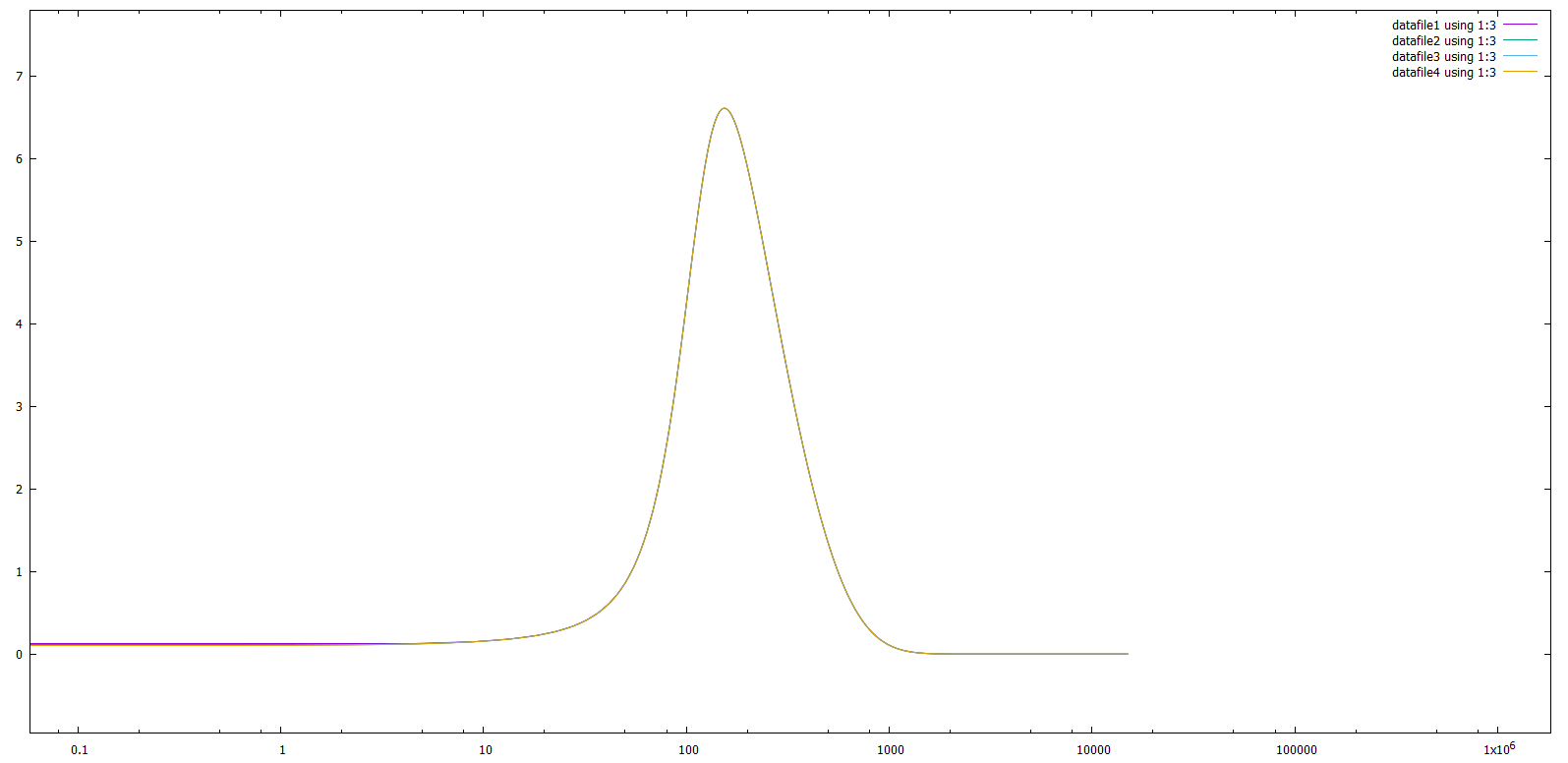 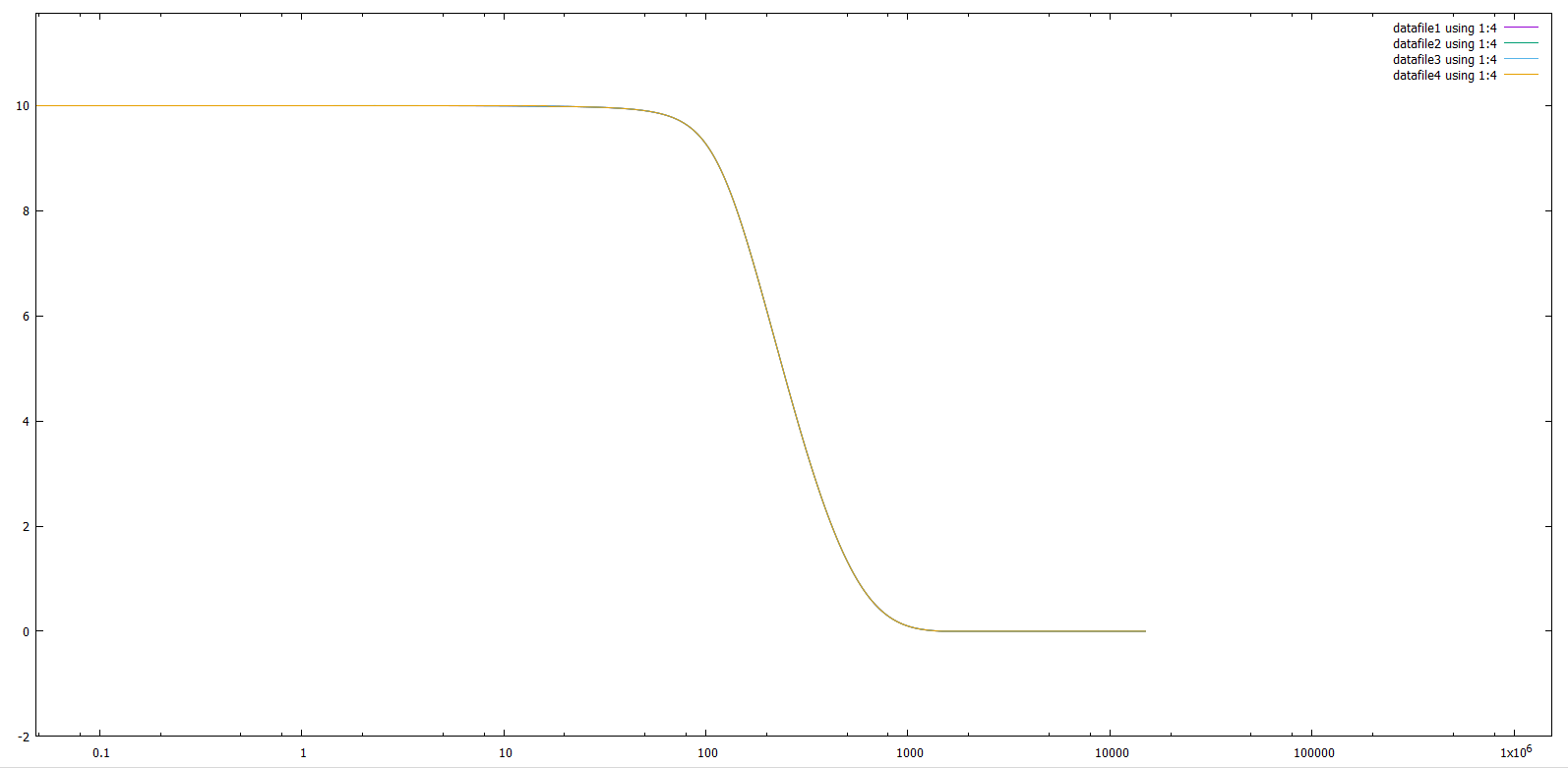 |
