Задачи 1
по курсу "Математическая обработка результатов химического эксперимента"
Основные задачи математической статистики:
1) восстановление закона распределения непараметрическими методами;
2) оценивание параметров распределения (параметрические методы);
3) проверка состоятельности гипотезы о законе распределения.

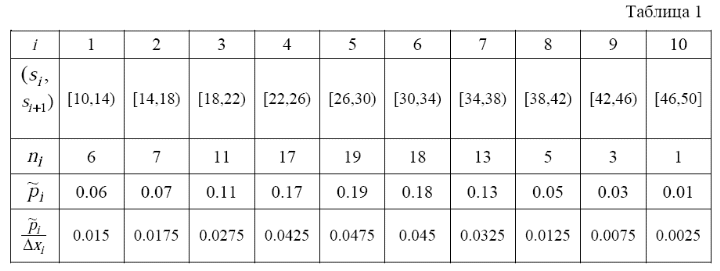
Для определенности считаем, что левые границы строго включены в интервалы, а правые нестрого. Если значение из выборки совпадает с левой границей, то оно входит в интервал, если совпадает с правой границей, то относится к следующему интервалу. В последний интервал включается также самая правая граница.
В таблице 1 представлен статистический ряд.
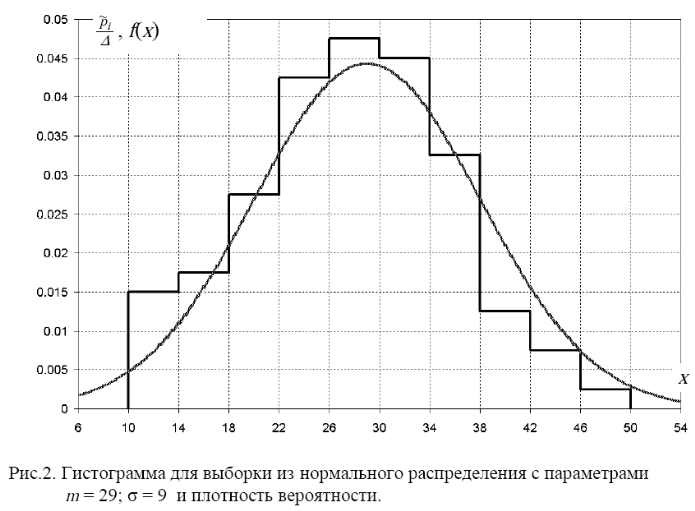
На рисунке 2 совместно изображены гистограмма и плотность
вероятности для случайной величины, реализациями которой является данная выборка (нормальная плотность с параметрами m = 29; σ = 9).

Практическая работа 1
Для выполнения заданий использовать данные из таблицы 2.
1. Построить график эмпирической функции распределения. Построить график функции распределения.
2. Найти оценку математического ожидания, а также несмещённые оценки дисперсии при известном и неизвестном математическом ожидании.
3. Построить доверительные интервалы для математического ожидания и стандартного отклонения при известном и неизвестном втором параметре соответственно.
Таблица 2
№
|
n
|
выборка
|
η
|
m
|
σ
|
0
|
12
|
1,8; 2; 3,3; 2,6; 1,3; -4; 0,5; 0,7; -0,7; 5,1; 5,7; 2
|
0,9
|
1,5
|
2,5
|
1
|
15
|
-6; -4,4; -2; -7,6; -0,4; 0,1; -3,7; -5,4; -0,8; -3,9; -5,3; -0,3; -4,8; -8,6; -0,9
|
0,95
|
-4
|
2
|
2
|
10
|
25; 27; 25; 20; 30; 25; 20; 23; 26; 22
|
0,9
|
25,2
|
3,4
|
3
|
12
|
-93; 52; 192; 79; 150; 102; -147; -165; -16; 105; 144; 162
|
0,95
|
10,5
|
102,1
|
4
|
14
|
73; -16; -66; 38; -85; -11; 24; 93; 112; 1; 15; 36; -7; 70
|
0,99
|
14
|
45
|
5
|
11
|
0; 9; 2,4; -1,7; 5; 5,4; 3,4; 5,7; 12,5; 4,5; 6,9
|
0,9
|
5
|
5
|
6
|
10
|
3,2; -0,5; 2; 1,6; 1,1; 2,7; 1,6; 0; 1,7; 4,8
|
0,9
|
1
|
2
|
7
|
12
|
8,33; 8,36; 8,23; 8,42; 7,95; 8,16; 8,32; 8,21; 8,27; 8,08; 8,09; 8,02
|
0,95
|
8,2
|
0,1
|
8
|
10
|
0,108; 0,093; 0,11; 0,117; 0,12; 0,089; 0,113; 0,111; 0,092; 0,091
|
0,9
|
0,1
|
0,01
|
9
|
15
|
-0,87; 0,4; -2,7; -0,01; 1,25; -0,9; 0,58; -0,61; 1,25; -1,04; -0,62; -0,19; -0,16; 2,31; 1,05
|
0,95
|
0
|
1,4
|
10
|
11
|
298; 322; 331; 346; 299; 337; 318; 313; 329; 304; 317
|
0,9
|
315
|
17
|
11
|
17
|
25; 29; 19; 26; 23; 16; 20; 22; 24; 18; 18; 30; 19; 26; 24; 24; 19
|
0,99
|
22
|
4
|
12
|
12
|
102; 39; -111; 87; 150; -76; 164; 151; 60; 127; 149; 94
|
0,9
|
100
|
100
|
13
|
10
|
-1,38; -2,21; -0,8; -0,1; -0,21; -0,54; -0,98; -3,05; -0,08; -0,19
|
0,9
|
-1
|
1
|
14
|
14
|
0,75; 0,34; 0,8; 0,86; 0,55; 0,43; 0,34; 0,84; 1,04; 0,58; 1,25; 0,76; 0,82; 1,16
|
0,95
|
0,8
|
0,25
|
15
|
11
|
-1,56; -1,73; -1,72; -1,54; -0,7; -1,58; -1,04; -1,18; -1,83; -1,51; -1,99
|
0,95
|
-1,5
|
0,3
|
16
|
12
|
3,59; 2,48; 2,35; 3,94; 3,58; 2,99; 3,75; 3,42; 3,33; 3,97; 2,98; 4,15
|
0,9
|
3,3
|
0,5
|
17
|
15
|
9,4; 7,3; 9,4; 8,4; 8,7; 5,7; 6,3; 5,3; -1,2; 5,2; 3,6; 4,3; 11,5; 6,5; 8,2
|
0,95
|
7
|
3
|
18
|
17
|
0,7; 1,4; -0,7; -1,5; 0,1; -0,1; -1; 0,1; 1,4; 0,9; -0,8; -0,3; 3; 0,3; -0,7; 0,1; 1,2
|
0,9
|
0
|
1
|
19
|
11
|
19,2; 20,1; 20,6; 19,4; 19,7; 19,1; 19,9; 18,7; 20,2; 19,8; 19,4
|
0,9
|
19,5
|
0,9
|
20
|
10
|
39,3; 21; 33,8; 34,9; 27,9; 20,6; 42,9; 30,2; 22,2; 23
|
0,9
|
32,2
|
7,3
| |
 Скачать 238 Kb.
Скачать 238 Kb.



