Решение задачи. ммтпур (1). Математические модели принятия управленческих решений Образец решения Задание
 Скачать 18.18 Kb.
|
|
Математические модели принятия управленческих решений Образец решения Задание Дано статистическое распределение выборки из генеральной совокупности объемом N=100 объектов.
Найти представительный объем выборки при 90%-ной надежности. Ответ дать в форме: 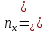 Решение Для данной выборки имеем: x_i 3 5 8 11 14 n_i 2 4 6 5 3 Сумма частот равна: n = ∑n_i = 20 Найдем среднее значение: x̄ = (∑(x_i * n_i)) / n = (32 + 54 + 86 + 115 + 14*3) / 20 = 8 Найдем дисперсию: σ^2 = (∑(x_i^2 * n_i) / n) - x̄^2 = (3^22 + 5^24 + 8^26 + 11^25 + 14^2*3)/20 - 8^2 ≈ 11.4 Найдем среднее квадратическое отклонение: σ = √(σ^2) ≈ 3.37 Найдем коэффициент вариации: V = (σ / x̄) * 100% ≈ 42% Для уровня доверия 90% и числа степеней свободы 19 (20-1), находим t_p(n) по таблице значений распределения Стьюдента: t_p(n) ≈ 1.73 Теперь можем вычислить представительный объем выборки: 1/n_x = 1/N + (ε / (t_p(n) * V))^2 где ε = 1 - 0.9 = 0.1 - это вероятность ошибки, которую мы готовы допустить. Подставляем значения: 1/n_x = 1/100 + (0.1 / (1.73 * 0.42))^2 1/n_x ≈ 0.01 + 0.018 1/n_x ≈ 0.028 n_x ≈ 1 / 0.028 n_x ≈ 36 Ответ: n_x = 36. Образец решения задания Дано статистическое распределение выборки из генеральной совокупности объемом N=100 объектов.
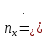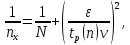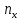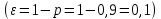Найти представительный объем выборки при 90%-ной надежности. Ответ дать в форме:  Решение Рабочая формула:  где  – представленный объем выборки  .Найдём среднее значение 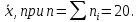 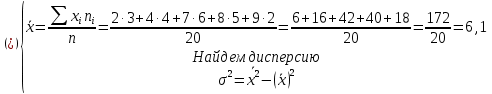 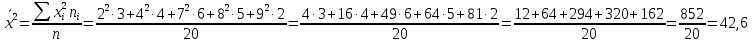 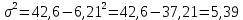 Найдем среднее квадратическое отклонение 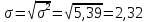 Найдем коэффициент вариации 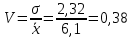 По таблице 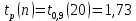 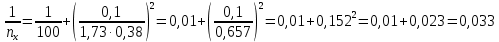 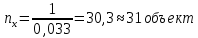 Вывод: Чтобы выборка с 90%-ной надежностью представляла генеральную совокупность нужно из 100 объектов случайным образом выбрать 31 объект. Ответ :  |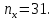
