Математический пакет matlab
 Скачать 163.98 Kb. Скачать 163.98 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра РАПС отчет по лабораторной работе №6 по дисциплине «Информатика» Тема: МАТЕМАТИЧЕСКИЙ ПАКЕТ Matlab
Санкт-Петербург 2020 Цель работы. Освоить технику работы с математическим пакетом Matlab. Основные теоретические положения. MATLAB – это приложения с графическим интерфейсом, имеющая среду и собственный язык технических расчетов, предназначенный для решения широкого спектра инженерных и научных задач любой сложности в любых отраслях. Язык MATLAB является высокоуровневым интерпретируемым языком программирования, включающим основанные на матрицах структуры данных, широкий спектр функций, интегрированную среду разработки, объектно-ориентированные возможности и интерфейсы к программам, написанным на других языках программирования. Ход работы: Простейшие вычисления Введя в Command Window простейшую математическую, операция 1+2 и нажав Enter, появится результат данной операции, записанный в переменную ans. Значение этой переменной можно увидеть в окне Workspace, в котором будут записаны значения всех переменных. 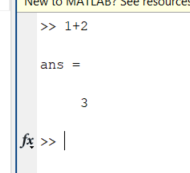  Чтобы продолжить работу с предыдущим выражением, например, вычислить (1+2)/4.5, то проще всего воспользоваться уже имеющимся результатом, который хранится в переменной ans. Для этого я набираю ans/4.5 и нажимаю Enter, получаю: 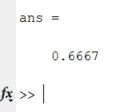 Форматы вывода результата вычислений Требуемый формат вывода результата определяется пользователем из меню MatLab. Для того, чтобы его изменить, выбираю в меню File пункт Preferences. Основные числовые форматы: Short – в этом случае результат показывается в виде числа и 4 чисел после десятичной точки. В MatLab возможна ситуация, когда при отображении слишком большого или малого числа результат не укладывается в формат short: 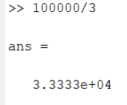 Результат 3.3333е+04 обозначает 3.3333·104. Long – используя этот числовой формат, результат будет отображаться в длинном формате с плавающей точкой long с четырнадцатью цифрами после десятичной точки. Форматы short e и long e предназначены для вывода результата в экспоненциальной форме с четырьмя и пятнадцатью цифрами после десятичной точки соответственно. Вычисления Задание 1: найти ребро куба, равновеликого шару, площадь поверхности которого равна площади боковой поверхности прямого кругового конуса, у которого высота вдвое меньше, чем длина образующей. Объем этого конуса равен 1. Для решения данной задачи использую основные геометрические формулы: Объём куба: Vkub = a^3 Объем шара: Vsh = (4/3)*π*R^3 Объем конуса: Vk = (1/3)*π*r^2*h Площадь боковой поверхности конуса: S = π*r*l Площадь поверхности шара: S = 4*π*R^2 Соотношение в конусе между радиусом основания, высотой и длиной образующей: r^2 + h^2 = l^2 С помощью формулы соотношения в конусе и условия, что у конуса высота вдвое меньше, чем образующая выведу формулу h=r/√3. Затем, подставив эту формулу в формулу объёма конуса, получу r= (Vk*3*√3/π)^1/3. Подставив это значение в Mathlab, получим результат: 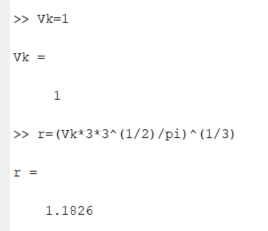 После этого в формулу l=2*h подставлю h=r/√3, получу l=(r∙2)/√3. Введём эту формулу в Mathlab:  Затем подставим r в формулу площади боковой поврхности конуса: 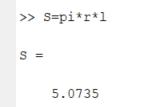 Теперь найдём из формулы площади шара радиус шара:  Так-как объём куба равен объёму шара, по условию, подставим в формулу a=Vsh^(1/3) радиус шара и получим результат: Ответ a=1.0243 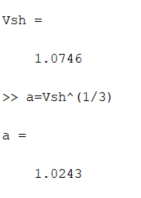 Задание 2: вычислить стоимость поездки на автомобиле на дачу (туда и обратно). Исходными данными являются: расстояние (rast) до дачи (км); количество бензина (potr), которое потребляет автомобиль на 100 км пробега; цена одного литра бензина (cena). Основная формула, используемая при расчете: sum=2·potr/100·rast·cena. Для решение данной задачи подбираю значения переменных: potr = 6.6 rast=120 cena=40. Подставим в MathLab:  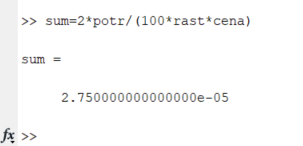 Подставив свои значения получу sum=2.750000000000000e-05. Задание 3: вычислить величину дохода по вкладу. Процентная ставка (% годовых) и время хранения (дней) задаются. Рассчитывать буду по формуле S=P*I*t/d*100, где S – доход по вкладу, P – первоначальная величина вклада, I – процентная ставка, t – количество дней, которой вклад будет находиться в банке, d – количество дней в году. Подставим значения P=36500, I=10, t=100, d=365, получим:   . . Ответ: S=1000. Задание 4: вычислить объем цилиндра. Заданы радиус основания r и высота цилиндра h. Основная формула, используемая при расчете. V=π·r2·h. Согласно условию, сам задам значения параметрам r и h, r=5, h=7:  или же 549.7787. Ответ: V=549.7787. или же 549.7787. Ответ: V=549.7787.Использование элементарных функций В MathLab есть возможность использовать тригонометрические, логарифмические и степенные функции, с помощью которых можно проводить различные расчёты. Эти функции я применил в следующем примере:  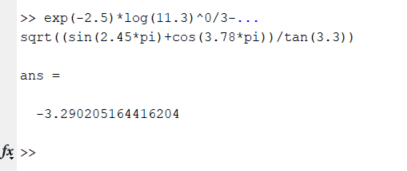 Чтобы внести изменения в формулу, которую я ввел ранее, можно нажать на клавишу ↑, которая вводит в командную последнюю введенную формулу. Благодаря этому я могу внести в нее изменения и сэкономить время. 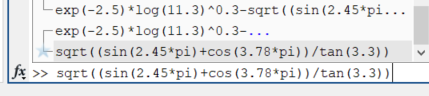 Выводы. Выполнив задания, можно сказать, что данная программа имеет отличную среду разработки и язык для проведения технических расчётов и решения различных задач. В этой программе удобно проводить различные математические операции. Мы научились проводить физические и геометрические расчёты, использовать тригонометрические, логарифмические и степенные функции, с помощью которых можно проводить различные расчёты. |
