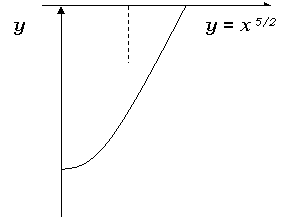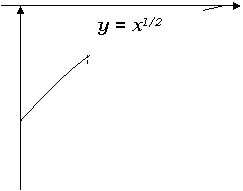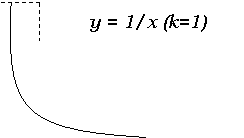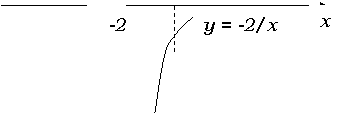Документ Microsoft Word. Реферат по математике Элементарные функции
 Скачать 79.18 Kb. Скачать 79.18 Kb.
|
|
Реферат по математике «Элементарные функции» план I. введение II. свойства и графики элементарных функций 1. Степенная функция 2. квадратичная функция 3. показательная функция 4. логарифмическая функция 5. обратно пропорциональная зависимость 6. тригонометрические функции III. мои примеры графиков IV. Список использованной литературы I. введение К элементарным функциям относятся рациональные, степенные, показательная и логарифмические функции, а также тригонометрические и обратные тригонометрические функции. К классу элементарных функций, кроме того относят также сложные функции, образованные из перечисленных выше элементарных функций. II. свойства и графики элементарных функций 1. степенная функция Степенной функцией называется функция вида f(x)=xa, где a - любое действительное число, называемое показателем степени. Свойства степенной функции. 1. Область определения степенной функции – множество всех положительных чисел. 2. Область значения степенной функции – множество всех положительных чисел. 3. Степенная функция непериодична, не является четной и не является нечетной. 4. Степенная функция непрерывна во всей области определения. 5. Степенная функция дифференцируема во всей области определения, и ее производная вычисляется по формуле (xa)¢= a. xa-1. 6. Степенная функция xa монотонно возрастает во всей области определения при a<0.
0 1 x 0 1 x Рис. 1 Рис. 2 7. При a<0 и a>1 график степенной функции направлен вогнутостью вверх, а при 0<a<1 – вогнутостью вниз. Графики степенной функции при некоторых значениях a приведены на Рис. 1 и Рис. 2. 2. квадратичная функция Функция f(x)=ax2+bx2+c, где a, b, c – некоторые действительные числа (a¹0), называется квадратичной функцией. График квадратичной функции называется параболой. Квадратичная функция может быть приведена к виду f(x)=a(x+b/2a)2-(b2-4ac)/4a, (1) выражение b2-4ac называется дискриминантом квадратного трехчлена. Представление квадратной функции в виде (1) называется выделением полного квадрата. Свойства квадратичной функции и ее график 1. Область определения квадратичной функции – вся числовая прямая. 2. При b¹0 функция не является четной и не является нечетной. При b=0 квадратичная функция – четная.
Рис. 3 Рис. 4 3. Квадратичная функция непрерывна и дифференцируема во всей области определения. 4. Функция имеет единственную критическую точку x=-b/(2a). Если a>0, то в точке x=-b/(2a) функция имеет минимум. При x<-b/(2a) функция монотонно убывает, при x>-b/(2a) монотонно возрастает. Если а<0, то в точке x=-b/(2a) функция имеет максимум. При x<-b/(2a) функция монотонно возрастает, при x>-b/(2a) монотонно убывает. Точка графика квадратичной функции с абсциссой x=-b/(2a) и ординатой y= -((b2-4ac)/4a) называется вершиной параболы. 5. Область изменения функции: при a>0 – множество значений функции [-((b2-4ac)/4a); +¥); при a<0 – множество значений функции (-¥;-((b2-4ac)/4a)]. 6. График квадратичной функции пересекается с осью 0y в точке y=c. В случае, если b2-4ac>0, график квадратичной функции пересекает ось 0x в двух точках (различные действительные корни квадратного уравнения); если b2-4ac=0 (квадратное уравнение имеет один корень кратности 2), график квадратичной функции касается оси 0x в точке x=-b/(2a); если b2-4ac<0, пересечения с осью 0x нет. Из представления квадратичной функции в виде (1) также следует, что график функции симметричен относительно прямой x=-b/(2a) – образа оси ординат при параллельном переносе r=(-b/(2a); 0). График функции f(x)=ax2+bx+c (или f(x)=a(x+b/(2a))2-(b2-4ac)/(4a)) может быть получен из графика функции f(x)=x2 следующими преобразованиями: а) параллельным переносом r=(-b/(2a); 0); б) сжатием (или растяжением) к оси абсцисс в а раз; в) параллельным переносом r=(0; -((b2-4ac)/(4a))). 3. показательная функция Показательной функцией называется функция вида f(x)=ax, где а – некоторое положительное действительное число, называемое основанием степени. При а=1 значение показательной функции при любом значении аргумента равно единице, и случай а=1 далее не будет рассматриваться. Свойства показательной функции. 1. Область определения функции – вся числовая прямая. 2. Область значения функции – множество всех положительных чисел. 3. Функция непрерывна и дифференцируема во всей области определения. Производная показательной функции вычисляется по формуле (ax)¢ =axlna 4. При а>1 функция монотонно возрастает, при а<1 монотонно убывает. 5. Показательная функция имеет обратную функцию, называемую логарифмической функцией. 6. График любой показательной функции пересекает ось 0y в точке y=1. 7. График показательной функции – кривая, направленная вогнутостью вверх.
График показательной функции при значении а=2 изображен на рис. 5 Рис. 5 4. Логарифмическая функция Функцию, обратную показательной функции y=ax, называют логарифмической и обозначают y=loga x. Число а называется основанием логарифмической функции. Логарифмическую функцию с основанием 10 обозначают lg x, а логарифмическую функцию с основанием е обозначают ln x. Свойства логарифмической функции. 1. Область определения логарифмической функции – промежуток (0; +¥). 2. Область значения логарифмической функции – вся числовая прчмая. 3. Логарифмическая функция непрерывна и дифференцируема во всей области определения. Производная логарифмической функции вычисляется по формуле (loga x)¢ = 1/(x ln a). 4. Логарифмическая функция монотонно возрастает, если а>1. При 0<a<1 логарифмическая функция с основанием а монотонно убывает. 5. При любом основании a>0, a¹1, имеют место равенства loga 1 = 0, loga a =1. 6. При а>1 график логарифмической функции – кривая, направленная вогнутостью вниз; при 0<a<1 – кривая, направленная вогнутостью вверх.
График логарифмической функции при а=2 изображен на рис. 6.
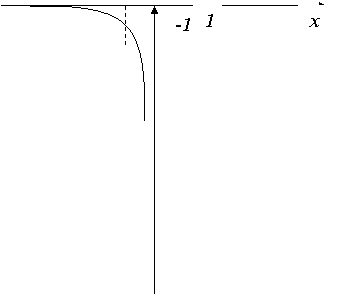
Рис. 6 Основное логарифмическое тождество. Обратной функцией для показательной функции y=ax будет логарифмическая функция x =loga y. По свойствам взаимно обратных функций f и f-I f(f-I (y))=y для всех x из области определения функции f-I(х). В частности, для показательной и логарифмической функции равенство (1) принимает вид alogay=y. Равенство (2) часто называют основным логарифмическим тождеством. При любых положительных х, у для логарифмической функции верны следующие равенства, которые могут быть получены как следствия основного логарифмического тождества (2) и свойства показательной функции: loga (x×y)=loga x+loga y; loga (x/y)= loga x-loga y; loga (xa)=a× loga x (a - любое действительное число); logaa=1; loga x =( logb x/ logb a) (b – действительное число, b>0, b¹1). В частности из последней формулы при а=е, b=10 получается равенство ln x = (1/(ln e))lg x. (3) Число lg e называют модулем перехода от натуральных логарифмов к десятичным и обозначают буквой М, а формулу (3) обычно записывают в виде lg x =M× ln x. 5. обратно пропорциональная зависимость Переменную y называют обратно пропорциональной переменной x, если значения этих переменных связаны равенством y = k/x, где k – некоторое действительное число, отличное от нуля. Число k называют коэффициентом обратной пропорциональности. Если считать x независимой переменной, а y – зависимой, то формула y = k/x определяет y как функцию от x. График функции y = k/x называется гиперболой.
Рис. 7 Свойства функции y = k/x. 1. Область определения функции – множество всех действительных чисел, за исключением числа 0. 2. Область значения функции – множество всех действительных чисел, за исключением числа 0. 3. Функция f(x) = k/x – нечетная, и ее график симметричен относительно начала координат. Функция f(x) = k/x непрерывна и дифференцируема во всей области определения. f(x)¢ = - k/x2. Функция критических точек не имеет. 4. Функция f(x) = k/x при k>0 монотонно убывает в (-¥, 0) и (0, +¥), а при k<0 монотонно возрастает в тех же промежутках. 5. График функции f(x) = k/x при k>0 в промежутке (0, +¥) направлен вогнутостью вверх, а в промежутке (-¥, 0) – вогнутостью вниз. При k<0 промежуток вогнутости вверх (-¥, 0), промежуток вогнутости вниз (0, +¥). График функции f(x) = k/x для значения k=1 изображен на рис. 7. 7. тригонометрические функции Функции sin a, cos a, tg a, ctg a называются тригонометрическими функциями угла a. Кроме основных тригонометрических функций sin a, cos a, tg a, ctg a существуют еще две тригонометрические функции угла a - секанс и косеканс, обозначаемые sec a и cosec a соответственно. sin х Синусом числа х называется число, равное синусу угла в радианах. Свойства функции sin х. 1. Область определения – множество всех действительных чисел. 2. Область значения – промежуток [-1; 1]. 3. Функция sin х – нечетная: sin (-х)=- sin х. 4. Функция sin х – периодическая. Наименьший положительный период равен 2p: sin (х+2p)= sin х. 5. Нули функции: sin х=0 при x=pn, n Î Z. 6. Промежутки знакопостоянства: sin х>0 при x Î (2pn; p+2pn), n Î Z, sin х<0 при x Î (p+2pn; 2p+2pn), n Î Z. 7. Функция sin х непрерывна и имеет производную при любом значении аргумента: (sin х)¢ =cos x. 8. Функция sin х возрастает при xÎ ((-p/2)+2pn; (p/2)+2pn), n Î Z, и убывает при xÎ ((p/2)+2pn; ((3p)/2)+ 2pn), n Î Z. 9. Функция sin х имеет минимальные значения, равные –1, при х=(-p/2)+2pn, n Î Z, и максимальные значения, равные 1, при х=(p/2)+2pn, n Î Z. График функции y=sin х изображен на рис. 8. График функции sin х называют синусоидой.
Рис. 8 Свойства функции cos х. 1. Область определения – множество всех действительных чисел. 2. Область значения – промежуток [-1; 1]. 3. Функция cos х – четная: cos (-х)=cos х. 4. Функция cos х – периодическая. Наименьший положительный период равен 2p: cos (х+2p)= cos х. 5. Нули функции: cos х=0 при x=(p/2)+2pn, n Î Z. 6. Промежутки знакопостоянства: cos х>0 при x Î ((-p/2)+2pn; (p/2)+2pn)), n Î Z, cos х<0 при x Î ((p/2)+2pn); ((3p)/2)+ 2pn)), n Î Z. 7. Функция cos х непрерывна и дифференцируема при любом значении аргумента: (cos х)¢ =-sin x. 8. Функция cos х возрастает при xÎ (-p+2pn; 2pn), n Î Z, и убывает при xÎ (2pn; p+ 2pn), n Î Z. 9. Функция cos х имеет минимальные значения, равные –1, при х=p+2pn, n Î Z, и максимальные значения, равные 1, при х=2pn, n Î Z.  График функции y=cos х изображен на рис. 9.
Рис. 9 Свойства функции tg х. 1. Область определения функции – множество всех действительных чисел, кроме числа х=p/2+pn, n Î Z. 2. Область значения – множество всех действительных чисел. 3. Функция tg х – нечетная: tg (-х)=- tg х. 4. Функция tg х – периодическая. Наименьший положительный период функции равен p: tg (х+p)= tg х. 5. Нули функции: tg х=0 при x=pn, n Î Z. 6. Промежутки знакопостоянства: tg х>0 при x Î (pn; (p/2)+pn), n Î Z, tg х<0 при x Î ((-p/2)+pn; pn), n Î Z. 7. Функция tg х непрерывна и дифференцируема при любом значении аргумента из области определения: (tg х)¢ =1/cos2 x. 8. Функция tg х возрастает в каждом из промежутков ((-p/2)+pn; (p/2)+pn), n Î Z, График функции y=tg х изображен на рис. 10. График функции tg х называют тангенсоидой.
Рис. 10 Свойства функции сtg х. 1. Область определения функции – множество всех действительных чисел, кроме чисел вида х=pn, n Î Z. 2. Область значения – множество всех действительных чисел. 3. Функция сtg х – нечетная: сtg (-х)=- сtg х. 4. Функция сtg х – периодическая. Наименьший положительный период функции равен p: сtg (х+p)= ctg х. 5. Нули функции: ctg х=0 при x=(p/2)+pn, n Î Z. 6. Промежутки знакопостоянства: ctg х>0 при x Î (pn; (p/2)+pn), n Î Z, ctg х<0 при x Î ((p/2)+pn; p(n+1)), n Î Z. 7. Функция ctg х непрерывна и дифференцируема при любом значении аргумента из области определения: (ctg х)¢ =-(1/sin2 x). 8. Функция ctg х убывает в каждом из промежутков (pn; p(n+1)), n Î Z. График функции y=сtg х изображен на рис. 11.
Рис.11 Свойства функции sec х. 1. Область определения функции – множество всех действительных чисел, кроме чисел вида х=(p/2)+pn, n Î Z. 2. Область значения: (-¥; 1]È[1; +¥). 3. Функция sec х – четная: sec (-х)= sec х. 4. Функция sec х – периодическая. Наименьший положительный период функции равен 2p: sec (х+2p)= sec х. 5. Функция sec x ни при каком значении аргумента не обращается в нуль. 6. Промежутки знакопостоянства: sec х>0 при x Î ((-p/2)+2pn; (p/2)+2pn), n Î Z, sec х<0 при x Î ((p/2)+2pn; (3p/2)+2pn), n Î Z. 7. Функция sec х непрерывна и дифференцируема при любом значении аргумента из области определения функции: (sec х)¢ =sin x/cos2 x. 8. Функция sec х возрастает в промежутках (2pn; (p/2)+ 2pn), ((p/2)+ 2pn; p+ 2pn], n Î Z, и убывает в промежутках [p+ 2pn; (3p/2)+ 2pn), ((3p/2)+ 2pn; 2p(n+1)], n Î Z.
График функции y=sec х изображен на рис. 12.
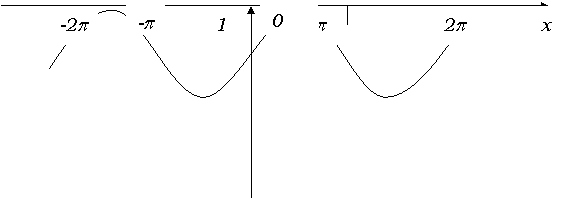
Рис. 12 Свойства функции cosec х. 1. Область определения функции – множество всех действительных чисел, кроме чисел вида х=pn, n Î Z. 2. Область значения: (-¥; -1]È[1; +¥). 3. Функция cosec х – нечетная: cosec (-х)= - cosec х. 4. Функция cosec х – периодическая. Наименьший положительный период функции равен 2p: cosec (х+2p)= cosec х. 5. Функция cosec x ни при каком значении аргумента не обращается в нуль. 6. Промежутки знакопостоянства: cosec х>0 при x Î (2pn; p+2pn), n Î Z, cosec х<0 при x Î (p+2pn; 2p(n+1)), n Î Z. 7. Функция cosec х непрерывна и дифференцируема при любом значении аргумента из области определения функции: (cosec х)¢ =-(cos x/sin2 x). 8. Функция cosec х возрастает в промежутках [(p/2)+ 2pn; p+ 2pn), (p+ 2pn; (3p/2)+ 2pn], n Î Z, и убывает в промежутках (2pn; (p/2)+ 2pn], ((3p/2)+ 2pn; 2p+2pn), n Î Z.
График функции y=cosec х изображен на рис. 13.
Рис. 13 III. мои примеры графиков График степенной функции.
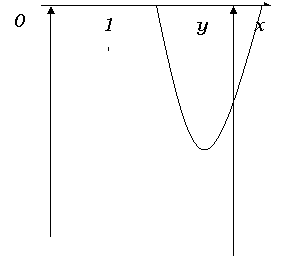
График квадратичной функции.
График показательной функции
График логарифмической функции
График функции y=k/x
IV. Список использованной литературы 1. A. Г. Цыпкин «Справочник по математике», М., 1979 г. 2. «Алгебра», М., 1981 г. 3. «Алгебра и начала анализа», М., 1991 г. |