Математическое моделирование экономических процессов с помощью парных регрессионных моделей расчетно-графическая работа. Математическое моделирование экономических процессов с помощью п. Математическое моделирование экономических процессов с помощью парных регрессионных моделей
 Скачать 248.06 Kb. Скачать 248.06 Kb.
|
|
Министерства науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Уфимский государственный нефтяной технический университет Кафедра: «Информационные технологии и прикладная математика» Расчётно – графическая работа № 2 по дисциплине «Математическое моделирование в задачах нефтегазовой отрасли» на тему: «Математическое моделирование экономических процессов с помощью парных регрессионных моделей» Вариант №25 Выполнил: ст.гр. МГГ61-21-01 Д.Е.Хуснутдинов Проверил: доцент, канд. наук А.А. Гималтдинова Уфа 2021 Расчетно - графическая работа № 2 Раздел «Элементы корреляционно – регрессионного анализа» Математическое моделирование экономических процессов с помощью парных регрессионных моделей В-25
Решение: 1. Вычисление коэффициента корреляции 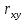 проведем по формуле: проведем по формуле: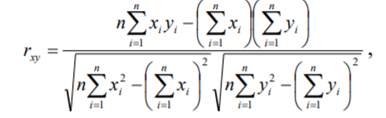 а расчёт параметров 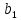 и и 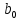 выборочного уравнения парной регрессии соответственно по формулам: выборочного уравнения парной регрессии соответственно по формулам: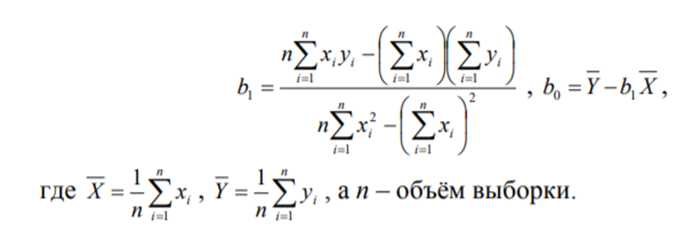 Для расчётов удобно использовать следующую таблицу: Таблица 1 - Вспомогательная таблица для расчёта параметров уравнения парной регрессии
Таблица 1- Вспомогательная таблица для расчёта параметров уравнения парной регрессии
Используя результаты вычислений, представленные в таблице 1, найдём значение выборочного коэффициента корреляции: 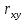 = = 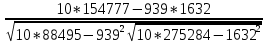 = 0,902; = 0,902;Полученное значение коэффициента корреляции свидетельствует о том, что между переменными X и Y имеется высокая корреляционная связь 2. Для оценки значимости коэффициента корреляции следует использовать статистику: t = 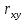 · ·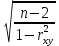 = 0,902· = 0,902·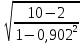 = 5,9; = 5,9;Используя таблицы распределения Стьюдента при заданном уровне надежности γ = 0,95 (γ = 1 - α) и числе степеней свободы, равном 8, определим критическое значение статистики: 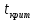 = 2,31; = 2,31;Поскольку │ 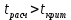 │ то нулевую гипотезу о равенстве нулю коэффициента корреляции отвергаем с вероятностью ошибки меньше 5% и делаем вывод о значимости коэффициента корреляции. │ то нулевую гипотезу о равенстве нулю коэффициента корреляции отвергаем с вероятностью ошибки меньше 5% и делаем вывод о значимости коэффициента корреляции.3. Для того чтобы составить выборочное уравнение прямой регрессии, необходимо вычислить коэффициенты 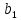 и и 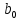 . Используя результаты расчётов, представленных в таблице 1, находим: . Используя результаты расчётов, представленных в таблице 1, находим: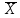 = = 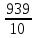 = 93,9 и = 93,9 и 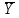 = = 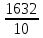 = 163,2; = 163,2;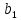 = = 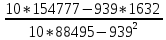 = 4,7451; = 4,7451; 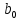 = 163,2 - 4,7451*93,9 = -282,367; = 163,2 - 4,7451*93,9 = -282,367;Таким образом, получается следующее регрессионное уравнение: Y = 4,7451*X - 282,367; 4. Прямая регрессии представлена на рисунке 1. 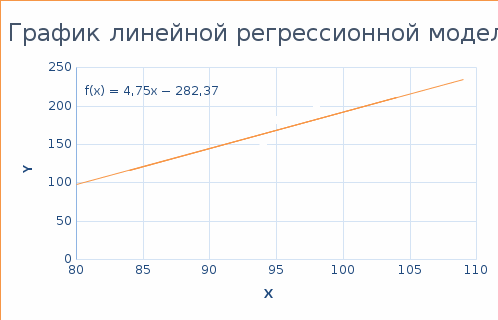 Рисунок 1 - График линейной регрессионной модели 5. Качество регрессионной модели может быть оценено с помощью коэффициента детерминации 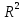 , определяется по формуле: , определяется по формуле: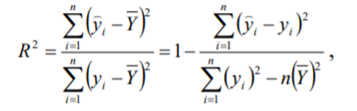 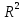 = 1 - = 1 - 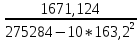 = 0,813; = 0,813;Коэффициент детерминации показывает, какую часть вариации (дисперсии) зависимой переменной Y воспроизводит (объясняет) построенное уравнение регрессии. В нашем случае построенное уравнение регрессии на 81,3% объясняет зависимость переменной Y от переменной X. 6. Проверка значимости регрессионной зависимости производится методом однофакторного дисперсионного анализа, где в качестве фактора выступает построенное уравнение регрессии. Результаты дисперсионного анализа принято представлять в виде стандартной таблицы 2. Таблица 2 - Результаты дисперсионного анализа 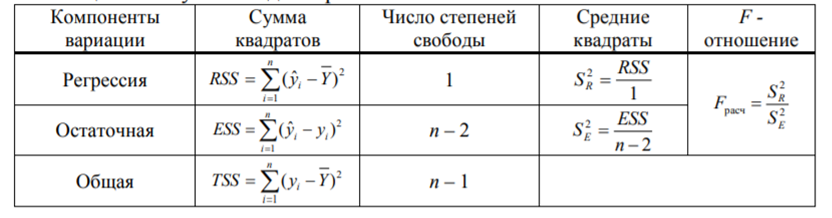 В нашем случае при расчёте сумм квадратов следует принять во внимание следующие равенства: 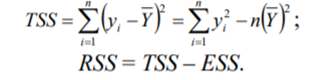 Тогда таблица дисперсионного анализа примет вид таблицы 3. Таблица 3 - Результаты дисперсионного анализа
Поскольку Fрасч превышает Fкрит, то делаем вывод о значимости уравнения регрессии. 7. Исправленные выборочные оценки стандартных отклонений (ошибок) МНК- коэффициентов регрессии вычисляются по формулам: 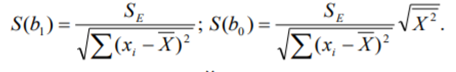 S( 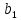 ) = ) = 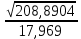 = 0,804; S( = 0,804; S(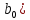 = 0,804*94,072 = 75,663; = 0,804*94,072 = 75,663;Доверительные интервалы для коэффициентов регрессии 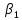 и и 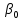 имеют соответственно вид: имеют соответственно вид:Доверительный интервал для 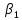 : [2,89; 6,6]; : [2,89; 6,6];Доверительный интервал для 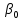 : [-456,846; -107,888]; : [-456,846; -107,888];Поскольку ни один из полученных интервалов не включает нулевое значение, делаем вывод о значимом отличии от нуля коэффициентов β1 и β0. 8. Интервал для прогноза среднего значения зависимой переменной при значении объясняющей переменной 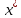 по линейному уравнению регрессии имеет вид: по линейному уравнению регрессии имеет вид:где 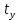 находят по таблицам критических точек распределения Стьюдента для заданных значений γ и числа степеней свободы ν = n - 2(в случае парной регрессии). Мы уже знаем, что при n=10 и γ=0,95(т.е α=0,05) находят по таблицам критических точек распределения Стьюдента для заданных значений γ и числа степеней свободы ν = n - 2(в случае парной регрессии). Мы уже знаем, что при n=10 и γ=0,95(т.е α=0,05) 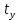 =2,31. =2,31.Вычисляем S( 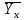 ) с учетом полученных ранее результатов: ) с учетом полученных ранее результатов:S( 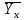 ) = ) = 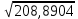 · ·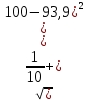 = 6,705; = 6,705;Из выборочного уравнения прямой регрессии имеем: 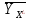 = 4,745*X - 282,3 = 4,745*100 - 282,3 = 192,145; = 4,745*X - 282,3 = 4,745*100 - 282,3 = 192,145;Получаем окончательный вид искомого доверительного интервала: [176,88;207,61] Для расчёта доверительного интервала возможных индивидуальных значений наблюдений при значении объясняющей переменной 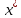 применяется формула: применяется формула:S( 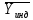 ) = ) = 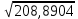 · ·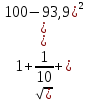 = 15,93; = 15,93;Окончательно получаем: [155,4; 288,89] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
