Математическое моделирование процессов, протекающих при электроконтактной сварке деталей с покрытиями

• Название: Математическое моделирование процессов, протекающих при электроконтактной сварке деталей с покрытиями
• Анкор: matematicheskoe-modelirovanie-elektricheskih-i-teplovyh-poley-pri
• Дата: 27.01.2022
• Размер: 1.7 Mb.
• Имя файла: matematicheskoe-modelirovanie-protsessov-protekayuschih-pri-elek.docx
• Тип: Документы; #343689
• страница: 3 из 5

Расчетное исследование

_  a

₂ , T(0, x)  T₀ , T(,0)  T₀  A,

x

(2)

Рассмотрим процессы, протекающие в си стеме, состоящей из электродов и вертикально расположенных плоских свариваемых деталей. Между элементами системы, а также между средой и левой границей, средой и правой гра ницей учитываются контактные термические и электрические сопротивления. Считается также общепринятым, что элементы системы имеют различные начальные температуры. В дополнение к этому полагаем следующее:

1. 
   температура в ядре зависит только от
   

продольной координаты, поток тепла квазиод

где x— координата, нормальная к оси x; T₀ — начальная температура; A — характерная вели чина скорости роста температуры на границе ядра.

Применяя к (2) преобразование Лапласа– Карсона






T*(s, x)  s_T(, x)exp(s)d,

0

получим следующую задачу:

²T*

номерный;

2. 
   потери тепла из ядра во вне не учитыва
   

T* sT₀ s a

;


 x²

ются;

3. 
   электрический ток распространяется
   

T*(s,0)  T₀

• 
  ^A.
  

s

(3)

в элементах системы по прямым линиям, ко торые могут либо расширяться, либо сужаться

Решение её имеет вид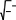

_A  _s

в зависимости от конфигурации элементов си

T*(s,0)  T₀  _sexp_{ a}x_.

стемы.

Согласно принятым допущениям в каждом из элементов (деталь, электрод) тепло распро страняется по закону

 

При этом мощность потока тепла в нор

мальном к xнаправлении вычисляется следу ющим образом:

T ²T

P*(s)   ^T*  A/ as.

_  a_x2  Q.

(1)

^x x0

Здесь: T — температура; τ — время; x — про дольная координата, начало которой распо лагается в левом крайнем сечении системы;

Соответственно,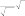

p p()   ^2A .

a
(4)

a = λ/(cρ) — коэффициент температуропро водности; ρ, λ, c — плотность, коэффициент теплопроводности, теплоемкость материала соответствующего элемента рассматриваемой системы; Q= Q(τ) = q(τ)/(cρ) — джоулево теп

ло; q()  (I/ S)² — удельная интенсивность

Следует иметь ввиду, что величина Aзави сит от процесса нагрева ядра [12]. В свою оче редь, он в значительной степени ослабляется потерями тепла на фазовые переходы, оттоком его из ядра; это определяется значениями пара метра A. Учитывая сказанное, вместо упрощен

джоулева тепловыделения; I — ток; S= S(x)—

ного уравнения (1) запишем

T_ ²T 2 p

3. 
   Между телами существует электриче
   

_ a_x2  Q _rc .

(5)

ское контактное сопротивление. Это приво дит к тому, что проходящий через контакт ток

Следующий важный вопрос — моделиро

вание тепловых процессов на стыке двух тел. Исходя из физических представлений, приве денных в научно-технической литературе [3], примем следующие допущения:

создает на нем разность потенциалов, и появ ляется дополнительное джоулево тепловыде ление. При условии, что потенциалы v₁, v₂ на поверхностях стыка с изменением радиуса r не меняются, имеем

1. 
   Два тела (рис. 2) контактируют на ограни
   

ченных площадках S(j_g, j) (j_g– номер границы,

I _

v₁  v_{2 ,}

(7)

слева направо j_g= (1, 2, …)); S(j_g, 1) — площадь

S( j_g, j) R_E (T₁,T₂ )

контакта до того, как расплавится металл с пер вой (левой) и второй (правой) стороны контак та; S(j_g, 2) — площадь после того, как металл расплавится хотя бы с одной стороны контакта.

2. 
   Между пластинами существует термиче ское контактное сопротивление, которое при
   

где R_E (T₁,T₂ ) — удельное электрическое сопро тивление, которое также зависит от давления сжатия.

Удельная мощность джоулевых тепловыде лений на контакте равна

2

водит к тому, что в сечении Sтемпературы слева

P  I(v v)  ^I R (T,T). (8)

(T₁) и справа (T₂) не совпадают, а мощность по



E
^{E1 2} S( j, j) ^{1 2}

g

тока тепла Q_kчерез стык выражается формулой

3. 
   Теплоемкостью межстыкового простран
   

Q_k (T₁ T₂ )S( j_g, j) / R_k(T₁,T₂ ),

(6)

ства пренебрежем ввиду ее малости. В резуль

где величина

R(T,T)

— удельное термиче

тате тепло, выделяющееся на контакте, не за

k 1 2

держивается, а «рассасывается» вбок, т.е.

ское контактное сопротивление, сильно зави сящее от давления сжатия деталей.

S_ j , j_  ^T1   ^{T2 }  P.
(9)


g  1 _x 2 _x E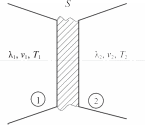

 

Наличие разности температур на стенках приводит к тому, что потоки тепла в левое тело отличаются от потоков в правое на ве личину 2Q_k. Это означает перераспределение потоков тепла: отнятая от одного тела величи на Q_k передается другому телу системы. Соот ветственно,

 ^T1  

^T2  2

T₁ T_{2 .}

(10)

¹ x

² x R_k(T₁,T₂ )

Из уравнений (9), (10) следует

^{ T1  0,5P}E^{ P,  T2  0,5P}E^{ P, (11)}

¹ x


k 2 _x k

^{где Pk= Pk(T1, T2) = (T1 –T2)/Rk(T1, T2); P}E^

 P_E/ S( j_g, j).

Рис. 2. Схема контакта двух тел:

S— область контакта; λ₁, λ₂, v₁, v₂ —

коэффициенты теплопроводности, потенциалы на границах S; T₁, T₂ — температура

материала на этих границах

Fig. 2. The scheme of contact of two bodies:

S— area of contact; λ₁, λ₂, v₁, v₂ — the coefficients

of thermal conductivity, potentials at the boundaries S; T₁, T₂ — material temperature at these boundaries

Эти два соотношения при условии, что ве личины I, S(j_g, j) и зависимости R_E= R_E(T₁, T₂) известны, замыкают задачу (5).