Математическое моделирование процессов, протекающих при электроконтактной сварке деталей с покрытиями
 Скачать 1.7 Mb. Скачать 1.7 Mb.
|
Обсуждение результатовДля расчета характеристик тепловых про цессов, описываемых представленными выше математическими моделями, используются ме тод конечных разностей и явная схема. При проведении вычислительных экспе риментов рассматривался наиболее типичный вариант электроконтактной сварки трех оди наковых плоских стальных деталей толщиной h = 8 · 10–4 м (рис. 3) со следующими средни ми теплофизическими характеристиками [13]: λ = 47 Вт/(м · град); c = 480 Дж/(кг · град); ρ = = 7700 кг/м3; a = 0,127 · 10–4 м2/сек. Начальная температура T0 предполагается также одинако вой, равной 20 °С. Электроды считаются бронзовыми (марка БРХЦР), водоохлаждаемыми. Расстояние от конца электродов до охлаждающей жидкости составляет 5 · 10–3 м. В начальный момент вре 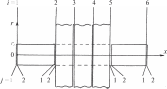 Рис. 3. Расчетная схема сварки трех деталей: i— но мер поверхности контакта; j — номер стороны по верхности контакта; x— продольная координата; r— поперечная (радиальная) координата; re— радиус мени они обладают температурой 100 °С; тем пература охлаждающей жидкости поддержи вается на уровне 10 °С. Согласно имеющимся в литературе данным по значениям λ , c, ρ , a электродов Fig. 3. The design scheme of welding of three parts: i — contact surface number; j — the number of the side of the contact surface; x— longitudinal coordinate; r— transverse E E E E (radial) coordinate; re— the radius of the electrodes для материала электродов выбраны значения λE = 55 Вт/(м · град); cE= 385 Дж/(кг · град); ρ = = 8500 кг/м3; a= 0,168 · 10–4 м2/сек; re= 0,0025 м. Удельное электрическое сопротивление стали — σ = 1,3 · 10–5 ом · м, бронзы — σe= 1,2 10–4 ом · м. Наличие покрытий учитывается в данных расчетах косвенно, скачкообразным измене нием термического, электрического сопротив лений, а также площадей контакта. В ходе экспериментов варьировалась, во-пер вых, форма импульса тока и его максимальное значение. Время импульса оставалось постоян ным, равным 0,15 сек. Во-вторых, менялась вели чина контактных термического и электрического сопротивлений, площади контакта, в том числе скачкообразно. Кроме того, расчеты проводи лись как со стоком тепла в радиальном направле нии в свариваемых деталях, так и без него. Когда в электродах и деталях в течение 0,15 сек ток остается постоянным (I = 7 кА), сток тепла в радиальном направлении отсут ствует, а между свариваемыми деталями имеет место так называемый «сухой» контакт (Rk= 0; S= 0,2 · 10–4 м2); RE3= RE4 1,0 · 10–9 ом · м2; RE1= RE2= RE5= RE6= 0. Расчет температуры в электродах и деталях для разных моментов времени в этом случае иллюстрирует рис. 4, a. Видно, что вблизи поверхностей контакта сва риваемых деталей температура значительно увеличивается, что характерно для подобных процессов. В целом же рост температуры ано мально большой, по всей видимости, из-за не учета стока тепла в радиальном направлении. При RE3 = 0,5 · 10–9 ом · м2, температура в общем уменьшается, появляется асимметрия тепло вой картины (рис. 4, б). Дальнейшее уменьшение RE3, RE4до 0,25 10–9 ом · м2 дает тепловые поля, показанные на рис. 5, a. Наконец, если учитывать электрическое сопротивление между деталями и электродами, то, полагая RE2 = RE5 = 0,25 · 10–9 ом · м2, получим достаточно реалистическую картину (рис. 5, б). Воспользовавшись приведенными здесь дан ными, можно определить время зарождения сва рочного ядра, проследить динамику его роста. В рассмотренных примерах удельное тер мическое контактное сопротивление приня то нулевым. Если же Rk1= Rk3= Rk4= Rk6= 0, а между электродами и деталями Rk2= Rk3= = 3,0 · 10–5 м2 · град/Вт, то детали оказывают ся как бы в тепловой изоляции, что видно на рис. 6. Далее предполагается, что импульс тока имеет трапецеидальную форму (рис. 7). Влия ние формы импульса на динамику изменения температуры в деталях и электродах можно проследить, сравнивая рис. 5, б и 8, a. Видно, что в случае трапецеидального импульса, в от личие от прямоугольного, вначале происходит медленный рост температур, затем достаточно быстрый разогрев, который потом замедляется вплоть до того, что начинается охлаждение де талей. 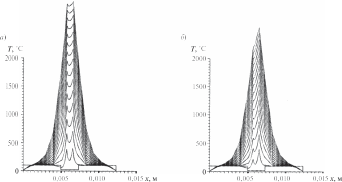 Рис. 4. Динамика изменения температуры в электродах и соединяемых деталях в отсутствие стока тепла в поперечном направлении при I= 7 кА: a— мощность джоулевых тепловыделений на участках контакта свариваемых деталей при RE3= RE4= 1,0 · 10–9 ом · м2; б— при RE3= 0,5 · 10–9 ом · м2, RE4= 1,0 · 10–9 ом · м2 Fig. 4. Dynamics of temperature change in electrodes and connected parts in the absence of heat sink in the transverse direction at I= 7 kA: a— the power of Joule heat release at the contact areas of welded parts at RE3= RE4= 1,0 · 10–9 Ω · m2; б— at RE3= 0,5 · 10–9 Ω · m2, RE4= 1,0 · 10–9 Ω · m2 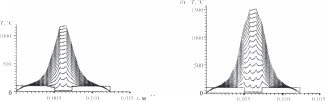  Рис. 5. Динамика изменения температуры в электродах и соединяемых деталях при a— RE3= RE4= 0,25 · 10–9 ом · м2; б— RE2= RE3= RE4= RE5= 0,25 · 10–9 ом · м2 Fig. 5. Dynamics of temperature changes in electrodes and connected parts at a— RE3= RE4= 0,25 · 10–9 Ω · m2; б— RE2= RE3= RE4= RE5= 0,25 · 10–9 Ω · m2 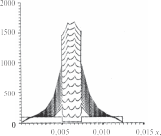 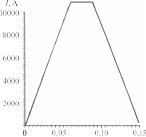 Рис. 6. Динамика изменения температуры в элек тродах и соединяемых деталей с учетом удельных термических контактных сопротивлений при Rk2= = Rk3= 3,0 · 10–5 м2 · град/Вт Fig. 6. Dynamics of temperature change in electrodes and connected parts taking into account specific thermal contact resistances at Rk2= Rk3= 3,0 · 10–5 m2 · deg / W Рис. 7. Трапецеидальное изменение импульса тока с течением времени (Imax = 12 кА) Fig. 7. Trapezoidal variation of the current pulse with time (Imax = 12 kA) 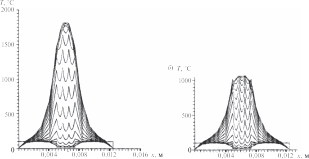 Рис. 8. Динамика изменения температуры в электродах и свариваемых деталях: a— при трапецеидальном импульсе тока RE2= RE3= RE4= RE5= 0,25 · 10–9 ом · м2; б— с учетом стока тепла в радиальном направлении Fig. 8. Dynamics of temperature change in electrodes and welded parts: a— with trapezoidal current pulse RE2= RE3= RE4= RE5= 0,25 · 10–9 Ω · m2; б — taking into account the heat flow in the radial direction 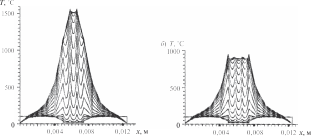 Рис. 9. Динамика изменения температуры в электродах и свариваемых деталях при трапецеидальном импульсе тока и учете стока тепла в радиальном направлении (RE3= RE4= 0,5 · 10–9 ом · м2): a— площадь контакта S2= S3= S4= S5= 0,2 · 10–4 м2; б— S2= S3= 0,2 · 10–4 м2, S3= S4= 0,3 · 10–4 м2 Fig. 9. The dynamics of temperature change in electrodes and welded parts with a trapezoidal current pulse and taking into account the heat flow in the radial direction (RE3= RE4= 0,5 · 10–9 Ω · m2): a— contact area S2= S3= S4= S5= 0,2 · 10–4 m2; б— S2= S3= 0,2 · 10–4 m2, S3= S4= 0,3 · 10–4 m2 Как уже отмечено выше, учет стока тепла в радиальном направлении может существенно понизить температуру в деталях. Эксперимен ты подтверждают это (см. рис. 8, aи 8, б). Увели чение же вдвое электрических контактных со противлений между деталями (RE3= RE4= 0,5 10–9 ом · м2) приводит к вполне приемлемым результатам (рис. 9, a). Что касается влияния площади контакта, то очевидно: уменьшение ее будет способствовать 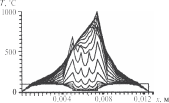 Рис. 10. Динамика изменения температуры в электродах и свариваемых деталях при учете расплавления материала покрытия Fig. 10. The dynamics of temperature changes in electrodes and welded parts, taking into account the melting of the coating material повышению температуры, а увеличение, нао борот, снижению. Действительно, увеличивая площадь контакта между деталями с 0,2 · 10–4 м2 до 0,3 · 10–4 м2 (S2= S5= 0,2 · 10–4 м2; S3= S4= = 0,3 · 10–4 м2) мы наблюдаем довольно сильное падение температуры (рис. 9, б). Согласно предлагаемому подходу имитация покрытий на поверхности деталей произво дится за счет скачкообразных изменений тер мического и электрического сопротивлений, а также площадей контакта при достижении определенной температуры. Учитывая, что температура плавления цинка около 500 °С, за критическую температуру примем это значе ние. В расчетах полагаем, что при температурах ниже 500 ºС RE2= RE5= 0,25 · 10–9 ом · м2; RE3= = RE4= 0,5 · 10–9 ом · м2; Rk2= Rk3= Rk4= Rk5= 1,0 10–8 м2 · град/Вт; S2= S5= 0,2 · 10–4 м2, S3= = S4 = 0,3 · 10–4 м2. При более высоких темпера турах RE2= RE3= RE4= 0,1 · 10–9 ом · м2; RE5= 0,25 10–9 ом · м2; Rk2= Rk3= Rk4= Rk5= 1,0 · 10–7 м2 град/Вт; S2= S3= S4= S5= 0,4 · 10–4 м2. Сле дует заметить, что возрастание сопротивлений и площадей контакта при расплавлении метал ла подтверждается литературными данными [3]. Полученные при указанных значениях па раметров результаты приведены на рис. 10. По сравнению со случаем неизменных ха рактеристик (рис. 9, a) максимальная темпера тура здесь упала почти на 30 %. Приблизитель но на столько же рекомендуется увеличивать величину тока при сварке покрытых деталей. |
