Описательная статистика. Описательная статистика (1). Математическое ожидание
 Скачать 47.93 Kb.
|
|
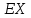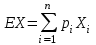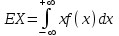Основными числовыми характеристиками случайных величин являются математическое ожидание  - среднее значение случайной величины Х и дисперсия  - мера отклонения от среднего.Математическое ожидание для дискретной случайной величины находится по формуле  , а для непрерывной случайной величины  .Дисперсией случайной величины Х называется  .Ковариацией случайных величин Х и Y называется:  Коэффициентом корреляции случайных величин Х и Y называется:  .X1,…,Xn - выборка из генеральной совокупности, E(Xi) = μ, D(Xi) = σ2, i = 1,…,n. Несмещенные оценки для математического ожидания и дисперсии (выборочное среднее и выборочная дисперсия) : 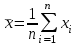 - выборочное среднее (является оценкой для EХ),  - оценка для D(X).Для двух выборок X1,…,Xn и Y1,…,Yn несмещенная оценка для ковариации случайных величин X и Y имеет вид:  - выборочная ковариация случайных величин Х и Y.Проверка значимости коэффициента корреляции: 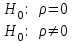 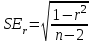 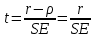 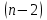 - степеней свободыКоэффициент вариации (Variation coefficient) 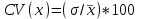 где σ – среднеквадратическое отклонение слу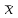чайной величины;  - ожидаемое (среднее) значение случайной величины.В статистике принято, что: если коэффициент вариации меньше 10%, то степень рассеивания данных считается незначительной; если от 10% до 20% - средней; больше 20% и меньше или равно 33% - значительной. Коэффициент асимметрии - 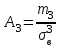  – куб стандартного выборочного отклонения,  – центральный эмпирический момент третьего порядка. Асимметрия симметричного распределения равно 0. 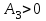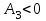если  , то распределение скошено вправо, если  – то влево. 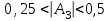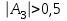Если полученное значение по модулю меньше, чем 0,25, то асимметрия незначительна, если  , то умеренная, и если  , то существенная.Эксцесс — показатель остроты пика графика распределения: 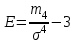 Эксцесс симметричного распределения равно 0 Если эксцесс больше 0, то график называется плосковершинным. Если эксцесс меньше 0, то график называется островершинным. |