Система M/M/n/0 представляет собой n- линейную СМО с r местами ожидания (r=0), в которую поступает пуассоновский поток интенсивности  , а времена обслуживания заявок независимы и при этом время обслуживания каждой заявки на любом приборе распределено по экспоненциальному закону с параметром , а времена обслуживания заявок независимы и при этом время обслуживания каждой заявки на любом приборе распределено по экспоненциальному закону с параметром  . В случае, когда . В случае, когда  , заявка, поступившая в переполненную систему (т.е. когда заняты все приборы и все места ожидания), теряется и вновь в нее не возвращаются. Система M/M/n/r также относится к экспоненциальным СМО. , заявка, поступившая в переполненную систему (т.е. когда заняты все приборы и все места ожидания), теряется и вновь в нее не возвращаются. Система M/M/n/r также относится к экспоненциальным СМО.
Уравнения, описывающие распределение заявок в системе
Рассматривая  -число заявок в системе в момент t, нетрудно показать, что процесс -число заявок в системе в момент t, нетрудно показать, что процесс  является однородным Марковским процессом с множеством состояний является однородным Марковским процессом с множеством состояний  . Ниже мы покажем, что процесс . Ниже мы покажем, что процесс представляет собой ПРГ. представляет собой ПРГ.
Выпишем систему дифференциальных уравнений Колмогорова. Для этого рассмотрим моменты t и  . Предполагая, что в момент t процесс v(t) пребывает в состоянии i, определим, куда он может попасть в момент . Предполагая, что в момент t процесс v(t) пребывает в состоянии i, определим, куда он может попасть в момент  , и найдем вероятности , и найдем вероятности  его переходов за время его переходов за время  . Здесь возможны три случая. . Здесь возможны три случая.
А. i процесс  не выйдет из состояния i равна произведению вероятности не выйдет из состояния i равна произведению вероятности  не поступления заявки за время не поступления заявки за время  на вероятность на вероятность  того, что за это время не обслужится ни одна из i заявок, т.е. равна того, что за это время не обслужится ни одна из i заявок, т.е. равна  . Вероятность перехода за время . Вероятность перехода за время  в состояние i+1 равна в состояние i+1 равна  - вероятности поступления заявки в систему. Наконец поскольку каждый прибор закончит за время - вероятности поступления заявки в систему. Наконец поскольку каждый прибор закончит за время  обслуживание находящейся в нем заявки с вероятностью обслуживание находящейся в нем заявки с вероятностью  , а таких приборов i, то вероятность перехода в состояние i-1 равна , а таких приборов i, то вероятность перехода в состояние i-1 равна  . Остальные переходы имеют вероятность . Остальные переходы имеют вероятность  . .
Б. n≤i остаться в состоянии i равна  , перейти в состояние i-1 за это же время , перейти в состояние i-1 за это же время

Таким образом, мы фактически доказали, что процесс  является процессом рождения и гибели с интенсивностями является процессом рождения и гибели с интенсивностями  при при  при при  и и  при при  . Обозначая через . Обозначая через  , распределение числа заявок в системе в момент t, получаем следующие выражения для , распределение числа заявок в системе в момент t, получаем следующие выражения для  в случае, когда в случае, когда  : :
 , ,
 , ,
 , ,

Если же  , то, что очевидно последнего выражения не будет, а в предпоследнем индекс i может принимать значения i=n,n+1,… . , то, что очевидно последнего выражения не будет, а в предпоследнем индекс i может принимать значения i=n,n+1,… .
Вычитая теперь  из обеих частей равенства, деля на из обеих частей равенства, деля на  и переходя к пределу и переходя к пределу
при  , получаем систему дифференциальных уравнений: , получаем систему дифференциальных уравнений:
 , ,
 , ,
 , (1.2) , (1.2)
 . .
Стационарное распределение очереди
В случае конечного r, например r=0, процесс  является эргодическим. Также он будет эргодическим в случае является эргодическим. Также он будет эргодическим в случае  при выполнении условия, о котором будет сказано ниже. Тогда из (1) при при выполнении условия, о котором будет сказано ниже. Тогда из (1) при  получаем, что стационарные вероятности состояний pi удовлетворяют систему уравнений: получаем, что стационарные вероятности состояний pi удовлетворяют систему уравнений:
 , ,
 , (1.3) , (1.3)
 , ,
 . .
Поясним теперь вывод системы уравнений (1.3), исходя из принципа глобального баланса. Так, например, согласно диаграмме переходов для фиксированного состояния i,  , имеем, что суммарные потоки вероятностей входящий в состояние i и выходящий из него равны, соответственно, , имеем, что суммарные потоки вероятностей входящий в состояние i и выходящий из него равны, соответственно,  и и  . .
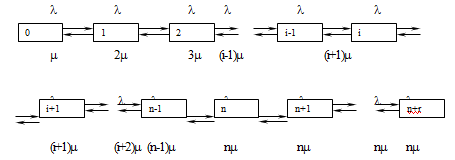
Рисунок 1 Диаграмма переходов
Исходя теперь из принципа локального баланса, что баланс потоков вероятностей между состояниями i и i+1 отражается равенствами :
 , ,
 , (1.4) , (1.4)
являющимися уравнениями локального баланса для данной СМО. Проверка справедливости равенств (1.4) производится непосредственным суммированием системы уравнений (1.3) по i при i=0,1,…,n+r-1.
Из соотношения (1.4), выражая рекуррентно вероятности  через через  , ,
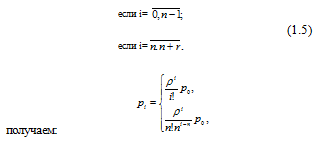
где  , а , а  определяется из условия нормировки определяется из условия нормировки  , т.е. , т.е.
 . (1.6) . (1.6)
Ясно, что формулы можно получить из общих соотношений для стационарных вероятностей состояний процесса рождения и гибели при указанных выше значениях  и и  . .
Если  , то стационарный режим существует при любом , то стационарный режим существует при любом  . .
Выпишем теперь выражения для некоторых характеристик очереди.
Стационарная вероятность  немедленного обслуживания заявки (обслуживания без ожидания) совпадает со стационарной вероятностью того, что в системе находится 0,1,…,n-1 заявок, т.е. немедленного обслуживания заявки (обслуживания без ожидания) совпадает со стационарной вероятностью того, что в системе находится 0,1,…,n-1 заявок, т.е.

Рассмотрим интересующий нас частный случай, когда r=0. тогда в системе отсутствуют места для ожидания (система с потерями M/M/n/0) и такая система носит название системы Эрланга. Система Эрланга описывает процессы, происходящие в простейших телефонных сетях, и названа так в честь А. К. Эрланга, впервые её исследовавшего. Для системы M/M/n/0 стационарные вероятности определяются формулой Эрланга
  , ,  . .
Следовательно, стационарная вероятность потери заявки определяется формулой:
 , ,
которую также называют формулой Эрланга.
Наконец, когда  , то мы имеем систему , то мы имеем систему  , для которой при любом , для которой при любом  стационарные вероятности существуют и, как следует из формул Эрланга при стационарные вероятности существуют и, как следует из формул Эрланга при  , имеют вид , имеют вид
 , ,  . .
Вернемся теперь к соотношениям (1.4). Суммируя эти равенства по i=0,1,…,n+r-1 , получаем
 , ,
где  - среднее число занятых приборов. Выписанное соотношение выражает равенство интенсивностей принятого в систему и обслуживаемого ею потоков в стационарном режиме. Отсюда мы можем получить выражение для пропускной способности системы - среднее число занятых приборов. Выписанное соотношение выражает равенство интенсивностей принятого в систему и обслуживаемого ею потоков в стационарном режиме. Отсюда мы можем получить выражение для пропускной способности системы  , определяемой как среднее число заявок, обслуженных системой в единицу времени, и называемой иногда интенсивностью выхода: , определяемой как среднее число заявок, обслуженных системой в единицу времени, и называемой иногда интенсивностью выхода:
 . .
Выражение для стационарного числа N заявок в системе нетрудно получить либо непосредственно из распределения вероятностей (4), либо воспользовавшись очевидным соотношением  . .
Стационарное распределение времени пребывания заявки в системе
Стационарное распределение W(x) времени ожидания начала обслуживания принятой в систему M/M/n/r заявки вычисляется практически так же, как и для системы  . Заметим, что заявка, заставшая при поступлении i других заявок в системе, немедленно начинает обслуживаться, если i времена. . Заметим, что заявка, заставшая при поступлении i других заявок в системе, немедленно начинает обслуживаться, если i времена.
Путем несложных преобразований находим, учитывая независимость времени обслуживания от времени ожидания начала обслуживания, находим, что стационарное распределение V(x) времени пребывания в системе принятой к обслуживанию заявки имеет ПЛС
 . .
Стационарные средние времена ожидания начала обслуживания  и пребывания заявки в системе и пребывания заявки в системе  задаются формулами: задаются формулами:
 , ,
 . .
Последнее выражение можно также получить из формул Литтла.
Нестационарные характеристики
Нестационарное распределение числа заявок в системе  получается интегрированием системы (1) с учетом начального распределения получается интегрированием системы (1) с учетом начального распределения  . .
Если  , то система (1) представляет собой линейную однородную систему обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами. , то система (1) представляет собой линейную однородную систему обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами.
Выходящий поток
В системе  , в установившемся режиме поток заявок, покидающих систему, является пуассоновским. То же самое можно сказать и о выходящем потоке из системы M/M/n/r, если понимать под ним суммарный поток как обслуженных, так и потерянных заявок. Доказательство этого с помощью метода обращения времени полностью совпадает с доказательством аналогичного факта для системы , в установившемся режиме поток заявок, покидающих систему, является пуассоновским. То же самое можно сказать и о выходящем потоке из системы M/M/n/r, если понимать под ним суммарный поток как обслуженных, так и потерянных заявок. Доказательство этого с помощью метода обращения времени полностью совпадает с доказательством аналогичного факта для системы  . .
|
 Скачать 7.32 Mb.
Скачать 7.32 Mb.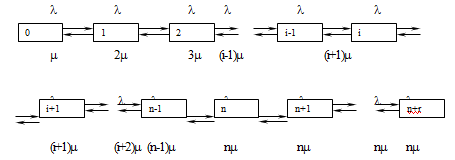
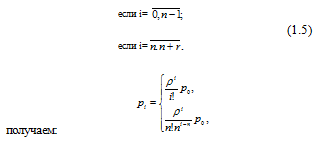
 . (1.6)
. (1.6) ,
,  ,
, .
. ,
,