баяндама. баяндама обл конференция. Математика сабаында оушыны логикасын дамыту утемисова Гулзира Сарсенгалиевна Математика пніні малімі
 Скачать 457.86 Kb. Скачать 457.86 Kb.
|
|
МАТЕМАТИКА САБАҒЫНДА ОҚУШЫНЫҢ ЛОГИКАСЫН ДАМЫТУ Утемисова Гулзира Сарсенгалиевна Математика пәнінің мұғалімі Ақтөбе облысы, Ойыл ауданы. Қарасу негізгі мектебі Қазір әлемде қарқынды өзгерістер болып жатыр. Атап айтатын болсақ саясат, медицина, өнер, экономика, техника мен технологиялар күн сайын даму үстінде. Қарқынды өзгеріп жатқан әлемге еліміз қалмай еріп жүруі үшін болашақ ұрпағымызды жеке тұлға ретінде дамытуымыз керек. Ал бұл дегеніміз біздер, яғни мұғалімдер оқушыларға білімдерді жай ғана беріп қоймай, оларды өз өмірлерінде ұтымды қолдана білуге үйрету. Барлық ғылымдардың ішінде адам өміріне үлкен әсер ететін - математика ғылымы. Сондықтан да әрбір оқушының алдында тұрған міндет – қазіргі заманғы математикалық логиканың негізін түсіне білу, логикалық есептерді шеше білу. Математикалық логиканы білмейінше, қазіргі қойылатын талаптарды ойдағыдай меңгеру қиын. Яғни біздің алдымызға қойған мақсатымыз , ол осы әлемдегі дамуға , өзгеруге сай оқушыларды қалай дайындасақ, дамытсақ ? Осындай қажеттіліктерді көре отырып, оқыту мен оқуға өзгеріс енгізе отырып, осы қиыншылықтарды шешу жолдарын іздестіруіміз керек. Оқушылардың ХХІ ғасыр талаптарына сәйкес келуі үшін ұстаздардың алдында тұрған негізгі міндеттердің бірі – қоғам құруға өзінің бар мүмкіндігін жұмсайтын шығармашыл, қабілетті маман дайындау. Әрине ондай мамандарды дайындау мектеп қабырғасынан бастау керектігі белгілі. Сондықтан да , әрбір оқушы математикалық сауатты болу керек, яғни математикалық іс-әрекеттің сипатына сай ойлауды қалыптастыру, қоғамдық өмір практикасына қажетті математикалық ойлауды қалыптастыру, математикалық білімді игеру мақсатында практикада қолдану, болмысты, табиғат пен қоғамды тануға қажет математикалық мазмұндай білу, есептерді шығаруға оптимальды жауап беруге дағдылану және ұмтылу керек. Білім беру саласында қол жеткізілген бүкіләлемдік білімнің мәні оқушылар үшін білімнің де, дағдылардың да тең дәрежеде маңызды екендігіне саяды. Заманауи тәсілдің негізгі ерекшелігі оқушылардың алған білімдерін жай ғана иеленіп қоймай, оларды орынды жерде қолдана білуіне басты назар аудару болып табылады, ал XXI ғасырда талап етілетін дағдылардың мәні осында. Қазіргі білім беру реформасы оқушыларда түйінді құзырлылықтарды қалыптастыруға бағытталған. Т.А. Эдисонның кезінде « Өркениеттің басты міндеті – адамды ойлауға үйрету» деп айтқанындай, білім негіздері мен еңбек құралдарын игеру ақыл-ой дағдыларынсыз мүмкін емес екені белгілі. Мұндай қабілеттің алғышарты логикалық сауаттылық болып табылады. Логикалық сауаттылық деген – кез келген интеллектуалдық қызметте қажет болатын логикалық білім-біліктердің жиынтығы. «Логика – ойлау адамгершілігі» деп берген Ж. Пиаженің анықмасынан логикалық сауаттылықтың тәрбиелік мәнін көреміз. Арнайы формуланы қолдануға келмейтін әрқайсысы өзінше талдау жасауды қажет ететін есептерді логикалық есептер дейді. Логикалық есептер әр түрлі математикалық конкурстарда, олимпиадаларда, жарыстарда жиі қолданылады. Ойлау қисыны жоғары адамдардың ерекше қасиеттерінің бірі – логикалық есептерді дұрыс шеше білу. Егер төменгі сыныптарда логикалық икемдіктер дұрыс қалыптаспаған болса, онда ол оқушылар жоғары сыныптарда үлгерімі төмендеп, математика бойынша есептер шығару барысында көп қиындықтар көреді. Ал логикалық сауаттылық дұрыс қалыптасқан болса, керісінше, бұрын нашар болса да, біртіндеп үлгерімі жоғарылап, математика бойынша жақсы жетістіктерге жетуі мүмкін. Мектепте оқушыларды логикалық сауаттылыққа үйрету қиынға соқпайды, әсіресе математика сабақтарында. Сонымен қатар, математика ғана емес, басқа пәндердің де бұл бағыттағы мүмкіндіктері аз емес. Олай болса барлық ұстаздардың мақсаты – оқушыларды әртүрлі қиындықтағы логикалық есептерді дұрыс шығара білуге үйрету. Жалпы логикалық есептер қалай шығарылады? Логикалық есептердің түрлері өте көп және шешу тәсілдері де әр түрлі. Сонымен қатар олардың шешу жолдарының жие қолданылатын үш тәсілі бар. Олар: тұжырымдар мен пайымдаулар көмегімен; кестелік тәсілді қолдану арқылы; алгебралық логика құралдары арқылы. Енді логикалық есептерді шығару барысында жие кездесетін әдістерді қарастырып көрейік. Логикалық есептерді кестелік тәсілді қолданып шығару. Бұл әдісті пайдалану барысында, есептің шартындағы мәліметтер мен жасалған пайымдаулар арнай кестеге түсіріледі. 1 – есеп. Мектепте тоғыз құмалақ ойыны бойынша жарыс өтті. Тоғыз құмалақ бойынша мектеп біріншілігіне 6 бала қатысты. Ақнұр, Абылай, Фариза, Ернат, Аяулым және Маркизат. Біріншілік айналу жүйесі бойынша өткізіледі – жарысқа қатысушы әрбір адам қалғандарымен бір-бір рет ойнап шығады. Бұған дейін бірнеше ойын өткізілген болатын: Ақнұр Абылаймен, Ернатпен, Маркизатпен; Фариза бұрын айтылғандай, Ақнұрмен және Ернатпен; Фариза - Ернатпен, Аяулым – Фаризамен және Маркизат – Ақнұрмен және Фаризамен ойнаған. Бұған дейін неше ойын ойналған және тағы неше ойын қалды? Шешуі: Кесте арқылы шығарайық.
Осы кесте бойынша « + » таңбасы көрсетілген ұяшықтарда ойналған ойындар саны болады, ал цифрларлармен белгіленген ұяшықтар енді болатын ойындар саны. Жауабы: 7 ойын ойналды, 8 ойын ойналады. Логикалық есептерді пайымдаулар көмегімен шығару. Бұл әдісті көбіне қарапайым логикалық есептерді шешу барысында қолданады. 2 – есеп. Математика пәнінен аудандық олимпиадаға қатысқан оқушылардан Мұрат, Ернұр, Назерке және Аружан алдыңғы төрт орынды алды. « Кім қандай орын алды » деген сұраққа қатысушылардың үшеуі, мынандай жауап берді: 1 – қатысушы: Назерке – 2; Аружан – 3, 2 – қатысушы: Назерке – 1; Ернұр – 2, 3 – қатысушы: Мұрат – 2; Аружан – 4. Бірақ бұл жауаптардың үшеуінің де бір бөлігі дұрыс, бір бөлігі қате болатын. Олай болса, осы төрт оқушының қайсысы қандай орын алған? Шешуі: 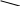 Егер Н – 2, А – 4. Ол жағдайда 3 – жауаптан М – 2. Бұл дұрыс емес. Ендеше, Н – 2 , сонда А – 3. Егер Н – 2, А – 4. Ол жағдайда 3 – жауаптан М – 2. Бұл дұрыс емес. Ендеше, Н – 2 , сонда А – 3. 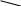 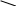 Бұдан шығатыны Н – 2 ; А -3 және М – 2; А – 4. Бұдан шығатыны Н – 2 ; А -3 және М – 2; А – 4. 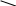  Ал Н – 2 болмағандықтан, Н – 1; Е – 2. Яғни Е – 4. Ал Н – 2 болмағандықтан, Н – 1; Е – 2. Яғни Е – 4.Жаубы: Назерке – 1 орын, Мұрат – 2 орын, Аружан – 3 орын, Ернұр – 4 орын алды. Логикалық есептерді алгебралық логика құралдары арқылы шығару. Бұл әдісте мектеп бағдарламасындағы ережелерді де қолданып, әрі қарай жетекші сұрақтар қойып отыра шығарады. 3 – есеп. Бір үш таңбалы сан цифрлар арқылы abc түрінде жазылған. Бұлардан құрастырылған төрт таңбалы abc1 және 2 abc сандары abc1 = 3 · 2 abc теңдігін қанағаттандырады. Осы abc санын табу керек. Шешуі: Сонда 2abc х 3 abc1 болатындай abc санын табу керек. Бұл есепті көбейту кестесін білетін логикасы жүйрік оқушы былай шығарады. Бірінші 3 – ке көбейткенде 1 – ге аяқталу үшін с = 7 болуы шарт. Яғни 2ab7 х 3 ab71 Енді қандай да бір b санын 3 – ке көбейтіп, оған ойдағы 2 санын қосқанда 7 – ге аяқталатын сан шығуы үшін b = 5 болуы керектігін табамыз, сонда 2a57 х 3 a571 Содан кейін қандай да бір а санын 3 – ке көбейтіп, оған ойдағы ойдағы 1 – ді қосқанда 5 шығу үшін а = 8 болуы шарт екенін табамыз. Ендеше 2857 х 3 8571 екені шығады. Жауабы: 857. Міне осындай есептерді шығара алатын оқушыларды түрлі олимпиадалармен жарыстарға «қорықпай» қатыстыруға болады. Яғни мұндай есептерді оқушыларды шошытып жібермейтіндей етіп жас ерекшеліктеріне, білім деңгейлеріне, қабілеттеріне қарай жеңілден күрделіге принципімен сатылап беру керек. Логикалық есептерді шешудің негізгі мақсаты – жас ұрпақ тәрбиесінің негізгі міндеттерінің бірі – баланың ойлау жүйесін ретке келтіріп, шыңдай түсу, өмірдің кез келген жағдайында дұрыс әрі ұтымды шешім таба алатындай ұшқыр ойлылыққа тәрбиелеу. Әдебиеттер: 1. «Мұғалім.kz» журналы. 2013ж, № 2 2. «Математика және логика» журналы. 2011ж, № 6 3. « Математика Қазақстан мектебінде» журналы. 2016ж, №2  |
