математика в формулах и таблицах. Математика в формулах и таблицах Справочное пособие
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Сибирский государственный университет телекоммуникаций и информатики В.И. Агульник, Б.П. Зеленцов МАТЕМАТИКАв формулах и таблицах Справочное пособиеНовосибирск 2000 г. В.И.Агульник, Б.П.Зеленцов. Математика в формулах и таблицах. Справочное пособие Справочное пособие содержит формулы, таблицы, графики по математике, охватывающие основные разделы элементарной математики - алгебры и геометрии. Оно предназначено для абитуриентов при подготовке к вступительным экзаменам, а также для студентов дневного и заочного обучения при изучении высшей математики и других дисциплин. Кафедра высшей математики Рецензент: И.И.Резван Утверждено редакционно-издательским советом СибГУТИ в качестве учебного пособия. Сибирский государственный университет телекоммуникаций и информатики, 2000 г. В.И.Агульник, Б.П.Зеленцов, 2000 г. ОГЛАВЛЕНИЕ
ЛИТЕРАТУРА ………………………………………………… 1. ЧИСЛА, ДРОБИ, МОДУЛИ n N - множество натуральных чисел d = НОД (n, m) - наибольший общий делитель n и m k = НОК (n, m) - наименьшее общее кратное n и m Z = Q = R – множество действительных чисел Арифметические операции с дробями: Пропорция Модуль числа. Определение: Свойства модуля:     a a+b a-b         a a+b a-b x 2. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ 3. СТЕПЕНИ И КОРНИ 4. КВАДРАТНЫЕ УРАВНЕНИЯ Корни уравнения: Формулы Виета: Разложение квадратного трехчлена на множители: Приведенное уравнение: Квадратное неравенство: Если D>0 , a>0, 5. ПРОГРЕССИИ Арифметическая прогрессия: Общий член: Сумма членов Геометрическая прогрессия Общий член: Сумма членов Сумма геометрической прогрессии (при Некоторые суммы: 6. ЛОГАРИФМЫ Логарифм числа Основное логарифмическое тождество: Свойства логарифмов: Десятичные логарифмы Натуральные логарифмы Логарифмические неравенства: Показательные неравенства: 7. ТРИГОНОМЕТРИЯ 7.1. Основные соотношения 7.2. Перевод из радианной меры углов в градусную и обратно: 7.3. Основные значения тригонометрических функций 7.4. Знаки тригонометрических функций     7.5. Формулы сложения 7.6. Формулы двойных углов 7.7. Формулы тройных углов 7.8. Формулы половинных углов Универсальная тригонометрическая подстановка, используемая для решения тригонометрических уравнений: 7.9. Формулы приведения
7.10. Формулы преобразования суммы и разности 7.11. Формулы преобразования произведения 7.12. Обратные тригонометрические функции 7.13. Простейшие тригонометрические уравнения1) Частные случаи: 2) Частные случаи: 3) 4) RefM499.doc8. Графики основных элементарных функций Парабола Гипербола Y  Y       y0 x0    x0 X     X  y0  Логарифмическая кривая Экспонента  Y   a>1 0  Y a>1   1  X 0 y = log a x y = ax  X Синусоида  Y             1      /2 - 2 X   y = sin x y = cos x  Y            Тангенсоида /2 0  X      y = ctg x y = tg x 10. ПЛАНИМЕТРИЯ
10.1.1. Основные соотношения A,B,C – вершины aa,b,c – стороны ,,  - углы - углытеорема проекций теорема синусов теорема косинусов 10.1.2. Замечательные линии и точки в теугольнике ma, mb, mc - медианы ha, hb, hc - высоты la, lb , lc - биссектрисы p - полупериметр, r - радиус вписанной окружности R – радиус описанной окружности 10.1.3. Формулы площади треугольника Разбиение треугольника медианами 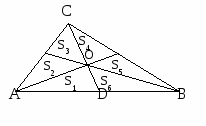 C A D B С 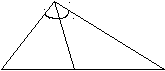 войство биссектрисы треугольника войство биссектрисы треугольника10.1.4. Прямоугольный треугольник a b c 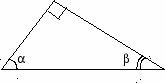 C A D B 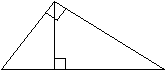 (CD - высота, опущенная на гипотенузу) Подобия в прямоугольном треугольнике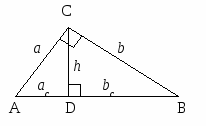 10.1.5. Правильный треугольник p=3a (p - периметр) 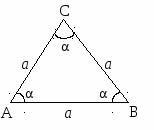 10.2. Четырехугольники 1 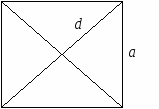 0.2.1. Квадрат 0.2.1. КвадратS=a2 10.2.2. Прямоугольник p=2(a+b) (p - периметр) S=ab 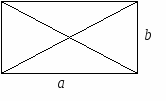 10.2.3. Параллелограмм 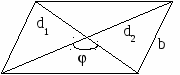 p=2(a+b) (p - периметр) p=2(a+b) (p - периметр)a  a 1  0.2.4. Ромб 0.2.4. Ромб1 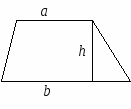 0.2.6. Трапеция 0.2.6. Трапеция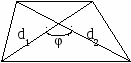 Свойства трапеции1. Во всякой трапеции середины оснований К, М лежат на прямой, проходящей через точку пересечения д 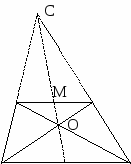 иагоналей О и точку пересечения иагоналей О и точку пересеченияпродолжений боковых сторон. K 2. Средняя линия трапеции параллельна о 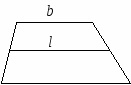 снованиям и равна их полусумме. снованиям и равна их полусумме.a 10.3. Окружность и круг. Д 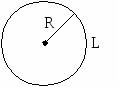 лина окружности лина окружностид 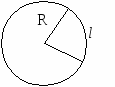 лина дуги окружности лина дуги окружности(n - величина дуги в градусах, - величина дуги в радианах). П 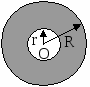 лощадь круга лощадь кругаплощадь кольца П 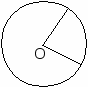 лощадь сектора лощадь сектораСвойства окружности 1) касательная и радиус, проведенный в точку касания, п  ерпендикулярны: r l ерпендикулярны: r l2) отрезки касательных, проведенные к окружности и  з точки, лежащей вне ее, равны, т.е. з точки, лежащей вне ее, равны, т.е.AB = AC 3 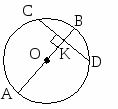 ) диаметр, перпендикулярный хорде, делит ее пополам; диаметр, проходящий через середину хорды, перпендикулярен ей. ) диаметр, перпендикулярный хорде, делит ее пополам; диаметр, проходящий через середину хорды, перпендикулярен ей.(AB) (CD) CK = KD 4 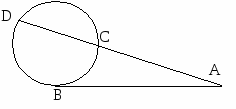 ) квадрат длины касательной равен произведению длины ) квадрат длины касательной равен произведению длинысекущей на ее внешнюю часть: AB2 = 5 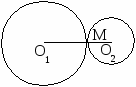 ) центры касающихся окружностей О1, О2 и точка их касания М лежат на одной прямой. ) центры касающихся окружностей О1, О2 и точка их касания М лежат на одной прямой.6 C ) в четырехугольник можно вписать окружность тогда и т 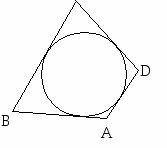 олько тогда, когда суммы длин противоположных олько тогда, когда суммы длин противоположных сторон равны, т.е.: AB + BC = AB + CD 7  ) около четырехугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна ) около четырехугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна1800, т.е.: Следствия из свойства 7): - из всех параллелограммов только около прямоугольника можно описать окружность; - около трапеции можно описать окружность тогда и только тогда, когда она равнобокая; 8) центральный угол измеряется градусной мерой дуги, на к  оторую он опирается: оторую он опирается:О = 9) величина вписанного угла 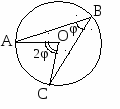 в два раза меньше центрального в два раза меньше центральногоугла, опирающегося на эту же дугу AOC = 2ABC 1  0) вписанные углы, опирающиеся на одну и ту же дугу, имеют одинаковую величину 0) вписанные углы, опирающиеся на одну и ту же дугу, имеют одинаковую величинуABD = ACD 11. СТЕРЕОМЕТРИЯ 1 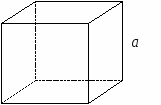 1.1. Куб 1.1. КубОбъем V = a3 Площадь поверхности S = 6a2 1 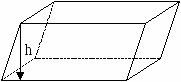 1.2. Параллелепипед 1.2. ПараллелепипедОбъем (S - площадь основания, h - высота) Прямоугольный параллелепипедО 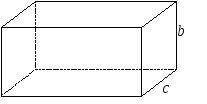 бъем бъемV = abc Площадь a S = 2(ab + bc + ac) d2 = a2 + b2 + c2; (d - диагональ) 1 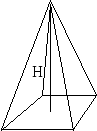 1.3. Пирамида 1.3. ПирамидаОбъем 11.4. Усеченная пирамида Объем 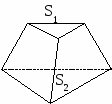 1 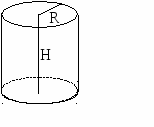 1.5. Цилиндр 1.5. ЦилиндрОбъем Боковая поверхность Площадь полной поверхности 11.6. Конус Объем Площадь полной поверхности  11.7. Усеченный конус О 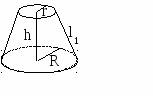 бъем бъемПлощадь полной поверхности 11.8. Сфера и шар Объём шара 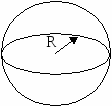 R– радиус сферы (шара) Площадь сферы ЛИТЕРАТУРА
Владимир Игоревич Агульник Борис Павлович Зеленцов Математика в формулах и таблицах. Справочное пособие. Редактор: В.К.Трофимов Корректор: Л.А.Подмогаева Лицензия ЛР – 020475, январь 1998 г. Подписано в печать Формат бумаги 62х84/16 Отпечатано на ризографе, шрифт №10 Изд.л.2, заказ № , тираж –500. Типография СибГУТИ, 630102, Новосибирск, ул Кирова, 86. |
