Высшая математика III этап. Материалы третьего этапа производная функции

• Название: Материалы третьего этапа производная функции
• Анкор: Высшая математика III этап.doc
• Дата: 17.10.2017
• Размер: 463.5 Kb.
• Имя файла: Высшая математика III этап.doc
• Тип: Документы; #9502
• Категория: Математика

ВЫСШАЯ МАТЕМАТИКА III ЭТАП 2006-07

МАТЕРИАЛЫ ТРЕТЬЕГО ЭТАПА

1. Производная функции

1. Найдите производную от функции:

2. Найдите производную от функции:

3. Найдите производную от функции:

4. Найдите производную от функции:

5. Найдите производную от функции:

6. Найдите производную от функции:

7. Найдите производную от функции:

8. Найдите производную от функции:

9. Найдите производную от функции:

10. Найдите производную от функции:

11. Найдите производную от функции:

12. Найдите производную от функции:

13. Найдите производную от функции:

14. Найдите производную от функции:

15. Найдите производную от функции:

16. Найдите производную от функции:

17. Найдите производную от функции:

18. Найдите производную от функции:

19. Найдите производную от функции:

20. Найдите производную от функции:

21. Найдите производную от функции:

22. Найдите производную от функции:

23. Найдите производную от функции:

24. Найдите производную от функции:

25. Найдите производную от функции:
2. Производная сложной функции.

1. Найдите производную от сложной функции: .

2. Найдите производную от сложной функции: .

3. Найдите производную от сложной функции: .

4. Найдите производную от сложной функции: .

5. Найдите производную от сложной функции: .

6. Найдите производную от сложной функции: .

7. Найдите производную от сложной функции: .

8. Найдите производную от сложной функции: .

9. Найдите производную от сложной функции: .

10. Найдите производную от сложной функции: .

11. Найдите производную от сложной функции: .

12. Найдите производную от сложной функции: .

13. Найдите производную от сложной функции: .

14. Найдите производную от сложной функции: .

15. Найдите производную от сложной функции: .

16. Найдите производную от сложной функции: .

17. Найдите производную от сложной функции: .

18. Найдите производную от сложной функции: .

19. Найдите производную от сложной функции: .

20. Найдите производную от сложной функции: .

21. Найдите производную от сложной функции: .

22. Найдите производную от сложной функции: .

23. Найдите производную от сложной функции: .

24. Найдите производную от сложной функции: .

25. Найдите производную от сложной функции: .

3. Дифференциал функции.

1. Найти дифференциал функции: .

2. Найти дифференциал функции: .

3. Найти дифференциал функции: .

4. Найти дифференциал функции: .

5. Найти дифференциал функции: .

6. Найти дифференциал функции: .

7. Найти дифференциал функции: .

8. Найти дифференциал функции: .

9. Найти дифференциал функции: .

10. Найти дифференциал функции: .

11. Найти дифференциал функции: .

12. Найти дифференциал функции: .

13. Найти дифференциал функции: .

14. Найти дифференциал функции: .

15. Найти дифференциал функции: .


4. Применение дифференциала к вычислению погрешностей при измерении физических величин.

1. При прямых измерениях найдено, что диаметр круга равен 6,67см, причём максимальная погрешность измерения составляет 0,03см. Найдите приближённую относительную погрешность диаметра в процентах.

2. Докажите, что относительная погрешность вычисленного объёма шара приблизительно равна утроенной относительной погрешности в измерении его диаметра.

3. Определите относительную погрешность, с которой допустимо измерить радиус шара, чтобы объём его можно было определить с точностью до 2%.

4. Период малых колебаний «нитяного» маятника (в секундах) определяется по формуле ,где l -длина маятника в сантиметрах, а g = 981 см/с² - ускорение силы тяжести. Докажите, что приближённая относительная погрешность периода колебаний маятника равна половине относительной погрешности его измеренной длины.

5. Пользуясь формулой , установите, насколько следует изменить длину маятника l = 25 см, чтобы его период увеличился на 0,05 секунд.

6. Из формулы следует, что определение ускорения силы тяжести с помощью маятника может быть вычислено по формуле Определите относительную погрешность в определении g, если известна относительная погрешность в измерении l, а погрешностью в измерении T можно пренебречь.

7.Из формулы следует, что определение ускорения силы тяжести с помощью маятника может быть сделано по формуле Определите относительную погрешность в определении g, если известна относительная погрешность в измерении T, а относительной погрешностью в l можно пренебречь.

8. Найдите абсолютную и относительную погрешности в определении объема шара, если при измерении его радиуса были получены значения R=(6,00,1)см.

9. Выведите формулу для вычисления относительной погрешности в измерении модуля упругости кости , где L, a,b,- измеряемые величины.

10. Выведите формулу для вычисления относительной ошибки в измерении коэффициента вязкости по методу Стокса , где ,R– измеряемые величины.

5. Частные производные. Полный дифференциал функции.

1. Вычислите частную производную функции

2. Вычислите частную производную функции

3. Вычислите частную производную функции

4. Вычислите частную производную функции

5. Вычислите частную производную функции

6. Вычислите частную производную функции

7. Вычислите частную производную функции

8. Вычислите частные производные и функции z = 2x²y + 3xy² + x³.

9. Вычислите частные производные и функции z = (x² + y²)³.

10. Вычислите частные производные и функции z = xy - .

11. Вычислите частные производные и функции z = .

12. Вычислите частные производные и функции z = x -3siny.

13. Докажите, что функция удовлетворяет дифференциальному уравнению в частных производных

14.Докажите, что закон гармонических колебаний x_t = Acos(ω₀t + φ₀) является решением уравнения гармонических колебаний: .

15.Докажите, что уравнение гармонической волны, распространяющейся в положительном направлении оси x, S(x,t) = S₀cos(ω₀(t -x/v)) является решением волнового уравнения: 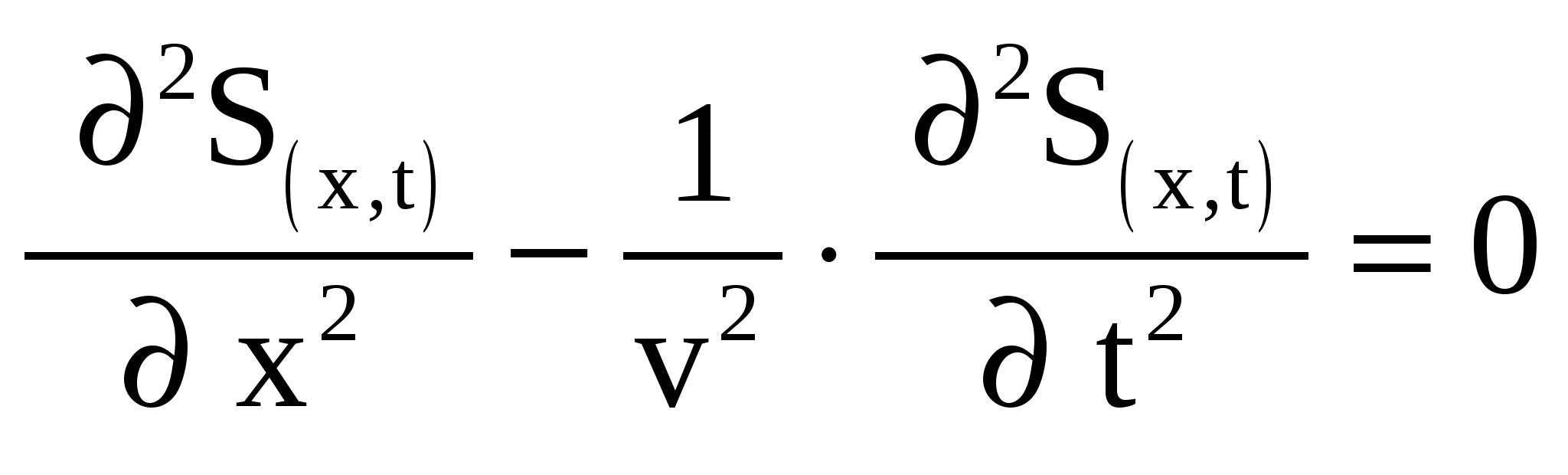, где v -фазовая скорость распространения волны.

16. Докажите, что функция удовлетворяет уравнению .

17. Найти полный дифференциал функции: .
18. Найти полный дифференциал функции: .

19. Найти полный дифференциал функции: .

20. Найти полный дифференциал функции: .

6. Интегральное исчисление.

1. Найдите интеграл: .

2. Найдите интеграл: .

3. Найдите интеграл: .

4. Найдите интеграл: .

5.Найдите интеграл: .

6. Найдите интеграл: .

7. Найдите интеграл: .

8. Найдите интеграл: .

9. Найдите интеграл: .

10.Найдите интеграл: .

11.Найдите интеграл: .

12.Найдите интеграл:.

13.Найдите интеграл:.

14.Найдите интеграл: .

16. Найдите интеграл: .

17. Найдите интеграл: .

18. Найдите интеграл: .

19. Найдите интеграл:.

20. Найдите интеграл: .

21. Найдите интеграл: .

22. Найдите интеграл: .

23. Найдите интеграл: .

24. Найдите интеграл: .

25. Найдите интеграл: .

26. Найдите интеграл: .

27. Найдите интеграл: .

28. Найдите интеграл: .

29. Найдите интеграл: .

30. Найдите интеграл: .

31. Найдите интеграл: .

32. Найдите интеграл: .

33. Найдите интеграл: .

34. Найдите интеграл: .

35. Найдите интеграл: .

36. Найдите интеграл: .

37. Найдите интеграл: .

38. Найдите интеграл: .

39. Найдите интеграл: .

40. Найдите интеграл: .

41. Вычислить определенный интеграл: ;

42. Вычислить определенный интеграл: ;

43. Вычислить определенный интеграл: ;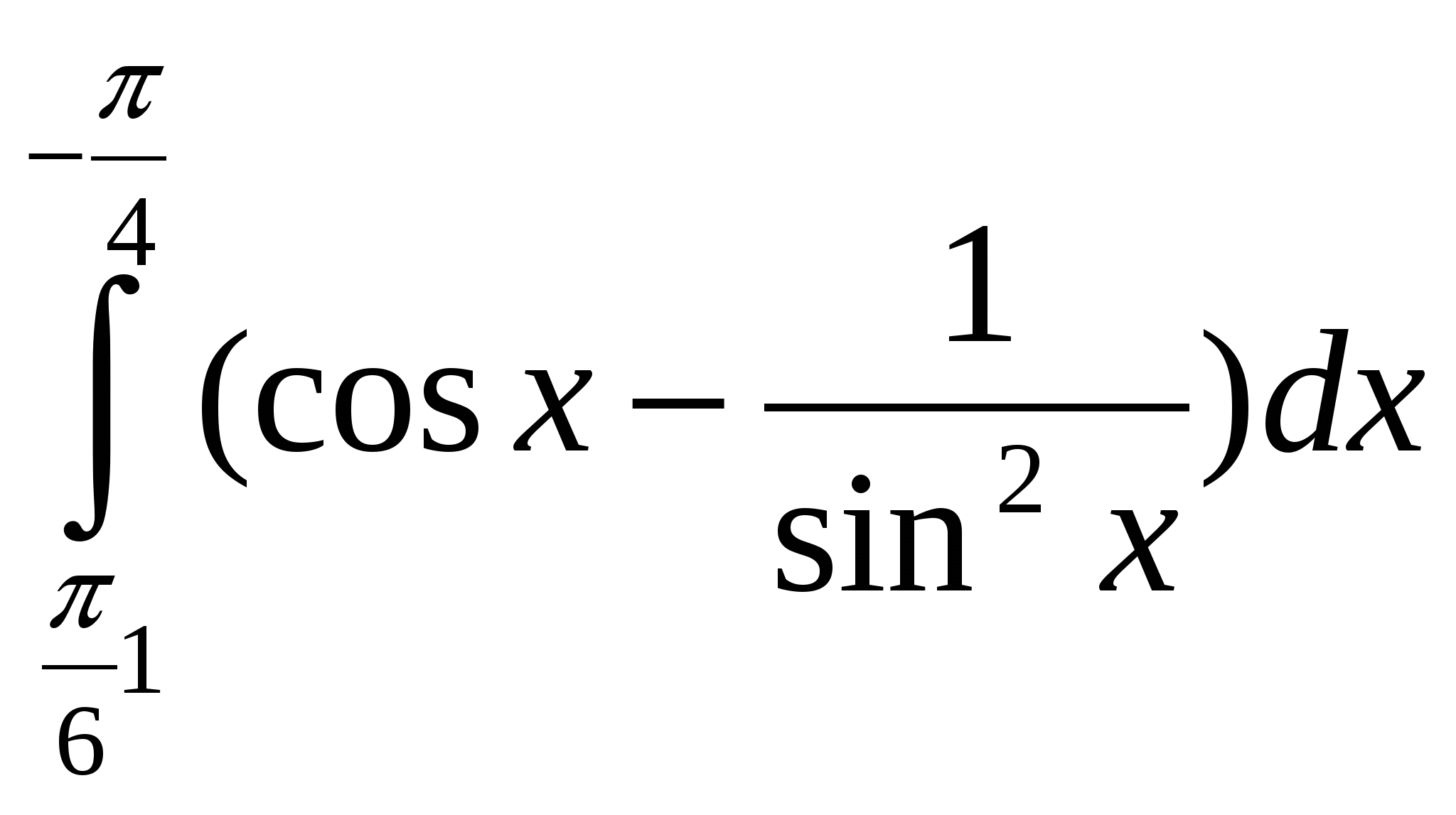

7. Дифференциальные уравнения.

1. Найти общее решение дифференциального уравнения: .

2. Найти общее решение дифференциального уравнения: .

3. Найти общее решение дифференциального уравнения: .

4. Найти общее решение дифференциального уравнения: .

5. Найти общее решение дифференциального уравнения: .

6. Найти общее решение дифференциального уравнения: .

7. Найти общее решение дифференциального уравнения: .

8. Найти общее решение дифференциального уравнения: .

9. Найти общее решение дифференциального уравнения: .

10. Найти общее решение дифференциального уравнения: .

11. Найти частные решения дифференциального уравнения: , если y =0 при x = 2.

12. Найти частные решения дифференциального уравнения: , если y =1+при x=е.

13. Найти частные решения дифференциального уравнения: , если y =6 при x = 9.

14. Найти частные решения дифференциального уравнения: , если y =1 при x = .

15. Найти частные решения дифференциального уравнения: , если y =2 при x = 0.

16. Найти частные решения дифференциального уравнения: , если y =3 при x = 0.

17. Найти частные решения дифференциального уравнения: , если y =8 при x = 1.

8.Задачи на составление дифференциальных уравнений.

1.Из реологического уравнения упруговязкой системы получите дифференциальное уравнение ползучести. Найдите общее решение полученного уравнения для относительной деформации. Решите задачу Коши, приняв за начальные условия отсутствие деформации в начальный момент времени. Схематически изобразите интегральную кривую, решенного Вами дифференциального уравнения.

2. Из реологического уравнения упруговязкой системы получите дифференциальное уравнение релаксации механического напряжения. Найдите общее решение полученного уравнения для напряжения. Решите задачу Коши, приняв за начальные условия напряжение σ₀ в момент времени t₀ = 0. Схематически изобразите интегральную кривую, решенного Вами дифференциального уравнения.

3. Из реологического уравнения вязкоупругой системы получите дифференциальное уравнение ползучести. Найдите общее решение полученного уравнения для относительной деформации. Решите задачу Коши, приняв за начальные условия отсутствие деформации в начальный момент времени. Схематически изобразите интегральную кривую, решенного Вами дифференциального уравнения.

4. Из реологического уравнения вязкоупругой системы получите дифференциальное уравнение упругого последействия. Найдите общее решение полученного уравнения для относительной деформации. Решите задачу Коши, приняв за начальные условия наличие относительной деформации ε₀ в начальный момент времени t₀ = 0. Схематически изобразите интегральную кривую, решенного Вами дифференциального уравнения.

5. Судебному медику необходимо установить момент смерти. При первом осмотре в 9 часов 30 минут местного времени была зафиксирована температура тела потерпевшего Т₁ = 35,5⁰ С, спустя один час температура тела оказалась Т₂ = 35,0⁰ С. Температура воздуха в помещении была постоянной и составляла Т₀ = 22⁰ С. Считать температуру тела в момент наступления смерти Т_N = 36,7⁰ С, а скорость охлаждения тела прямо пропорциональной разности температур тела в данный момент и окружающей среды.

6. Считая, что каждый элементарный слой вещества поглощает одну и ту же часть интенсивности попавшего на него электромагнитного излучения, составьте и решите дифференциальное уравнение для поглощения электромагнитного излучения. Идентифицируйте полученное частное решение дифференциального уравнения как закон поглощения Бугера.

7.Считая, что убыль изделий медицинской техники в процессе эксплуатации прямо пропорциональна исходному количеству изделий и промежутку времени эксплуатации, составьте и решите дифференциальное уравнение для вероятности безотказной работы изделия как функции времени. Идентифицируйте постоянный коэффициент в частном решении уравнения как интенсивность отказов медицинской техники.

8. Составьте дифференциальное уравнение для получения основного закона радиоактивного распада. Для чего считайте, что убыль распадающихся ядер прямо пропорциональна числу нераспавшихся к данному моменту ядер, а коэффициент пропорциональности обозначьте λ и назовите постоянной распада. Решите уравнение, получите частное решение в виде основного закона радиоактивного распада, учитывая , что в начальный момент времени t = 0 число нераспавшихся ядер было N₀. Постройте интегральную кривую.

9. По цилиндрической трубке малого радиуса (т.н. капилляру) стационарно в ламинарном режиме по действием разности давлений ∆P на концах трубки течёт ньютоновская жидкость с вязкостью η. Радиус трубки R, длина трубки l. Используя реологическое уравнение Ньютона , где τ - напряжение сдвига, - модуль градиента скорости, r- расстояние от оси трубки, составьте дифференциальное уравнение для линейной скорости течения жидкости по трубке v как функции расстояния от оси трубки v =v(r). Получите частное решение уравнения из условия, что на стенке трубки т.е. при r = R линейная скорость . Постройте интегральную кривую.

10. Считая известной зависимость линейной скорости течения V вязкой ньютоновской жидкости по цилиндрической трубке радиуса R:, где ΔP - разность давлений на концах трубки, η - вязкость жидкости, l - длина трубки, определите объёмную скорость течения (расход) жидкости Q. Идентифицируйте полученное решение уравнения как формулу Пуазейля.

11. Дифференциальное уравнение, составленное на основании второго закона Ньютона для движения материальной точки вдоль оси х имеет вид: где F- не зависит от времени, а m - масса. Найдите общее решение уравнения, изобразите решение графически .

12. Дифференциальное уравнение, составленное на основании второго закона Ньютона для движения материальной точки вдоль оси х имеет вид: где F- не зависит от времени, а m - масса. Найдите частное решение уравнения, если в начальный момент времени координата была равна нулю, начальная скорость равна нулю. Изобразите графически интегральную кривую.

13. Дифференциальное уравнение, составленное на основании второго закона Ньютона для движения материальной точки вдоль оси х имеет вид: где F- не зависит от времени, а m - масса. Найдите частное решение уравнения, если в начальный момент времени координата была равна нулю, начальная скорость равна V₀. Изобразите графически интегральную кривую.

14.Дифференциальное уравнение, составленное на основании второго закона Ньютона для движения материальной точки вдоль оси х имеет вид: где F- не зависит от времени, а m - масса. Найдите частное решение уравнения, если в начальный момент времени координата была равна Х₀, начальная скорость равна V₀. Изобразите графически интегральную кривую.

15. Скорость размножения бактерий пропорциональна количеству бактерий в рассматриваемый момент. В начальный момент имелось 100 бактерий и их число удвоилось в течении 3 часов. Найти зависимость бактерий от времени и во сколько раз увеличится количество бактерий в течении 9 часов.

16. Температура вынутого из печи тела в течении 20 минут падает от 200⁰С до 150⁰С. Температура воздуха равна 25⁰С. Через сколько времени от момента начала охлаждения температура тела понизится до 30⁰С, если скорость охлаждения тела пропорциональна разности температур тела и окружающей среды.

17. Закон распада лекарственного вещества в организме состоит в том, что скорость распада пропорциональна количеству лекарства. Известно, что половина первоначального количества распадается за время t₀. Какой процент лекарства окажется распавшимся через tчасов?

18.Получите выражение для тепловой мощности N_т , выделяемой при ламинарном течении ньютоновской жидкости вязкостью η по цилиндрической трубке длины l под действием разности давлений ΔP. Считайте известными так же радиус трубки R, удельную тепловую мощность , где - напряжение сдвига как функцию расстояния r от оси трубки и - скорость сдвига как функцию расстояния r от оси трубки.
9. Элементы теории вероятностей.

1.Студент разыскивает нужную ему формулу в 3-х справочниках. Вероятность того, что формула найдется в первом, втором и третьем справочнике, соответственно равны: 0,6; 0,7; 0,8. Найдите вероятность того, что формула содержится только в одном справочнике.

2. Студент разыскивает нужную ему формулу в 3-х справочниках. Вероятность того, что формула найдется в первом, втором и третьем справочнике, соответственно равны: 0,6; 0,7; 0,8. Найдите вероятность того, что формула содержится только в двух справочниках.

3. Студент разыскивает нужную ему формулу в 3-х справочниках. Вероятность того, что формула найдется в первом, втором и третьем справочнике, соответственно равны: 0,6; 0,7; 0,8. Найдите вероятность того, что формула содержится во всех 3-х справочниках.

4. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором, третьем справочнике, соответственно равны: 0,6; 0,7; 0,8. Найдите вероятность того, что формула не содержится ни в одном из трех справочников.

5.Студент разыскивает нужную ему формулу в трех спвочниках. Вероятности того, что формула содержится в первом, втором, третьем справочнике, соответственно равны 0,6; 0,7; 0,8. Найдите вероятность того, что формула содержится хотя бы в одном из трех справочников.

6.Радиологический метод лечения позволяет излечить от некоторого вида опухолей с вероятностью 0,7. Химиотерапия приводит к выздоровлению с вероятностью 0,8. Больной получает радиотерапию и с ним проводят курс химиотерапии одновременно. Какова вероятность излечения больного, если предположить, что эффективность радиотерапии не зависит от химиотерапии и наоборот?

7.Из стерилизатора наугад поочередно вынимают две иглы для инъекций. Известно, что при стерилизации 25% игл портится. В стерилизаторе находилось 20 игл. Определите вероятность того, что хотя бы одна из двух игл окажется хорошей.

8. Студент успел подготовить к экзамену 20 вопросов из 25. Какова вероятность того, что из трех, наудачу выбранных вопросов, студент знает не менее двух?

9.При дезинфекции использованы три вещества. Известно, что первое вещество уничтожает все патогенные микроорганизмы с вероятностью 0,7; второе – с вероятностью 0,75; третье – с вероятностью 0,8. Определите вероятность гибели всех патогенных микроорганизмов при одновременном применении всех трех веществ.

10.Абонент забыл последнюю цифру номера телефона и поэтому набирает ее наудачу. Найдите вероятность того, что ему потребуется сделать не более, чем две неудачные попытки.

11.Найдите вероятность того, что в семьях с двумя детьми оба ребенка – девочки. Считать, что вероятность рождения мальчика равна 0,515 и пол каждого последующего ребенка не зависит от пола предыдущих детей.

12. Вероятность попадания в цель при одном залпе из двух орудий равна 0,94. Найдите вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,7.

13.Задана функция плотности вероятности случайной величины, распределенной по нормальному закону: . Определите математическое ожидание.

14. Запишите выражение функции распределения вероятностей для нормально распределенной случайной величины, если ее математическое ожидание М(х) = - 1, а дисперсия D(x) = 9.
15.Случайная величина задана законом распределения:

Х	- 1	0	2	2,5
Р	0,2	0,3	0,4	0,1

Найдите вероятность Р(х < 2,5).

16.Задана функция плотности вероятности случайной величины, распределенной по нормальному закону: . Определите дисперсию.

1
7.Запишите выражение функции распределения вероятностей для нормально распределенной случайной величины, если ее математическое ожидание М(х) = 1, а дисперсия D(x) = 4.

18.Случайная величина задана таблицей:

Х	- 2	- 1	0	1	2
Р	0,05	0,15	0,1	0,5	0,2

Определите вероятность того, что она примет значения в промежутке: -1 < X < 1.

19.Задана функция плотности вероятности случайной величины, распределенной по нормальному закону: . Определите константу С.

20. Нарисуйте графики функции распределения вероятностей для 3-х случайных величин, распределенных по нормальному закону с математическим ожиданием М(х) = 0 и различными дисперсиями. Причем: .

21. Случайная величина задана таблицей:

Х	-2	-1	0	1	2
Р	0,05	0,15	0,1	0,5	0,2

Постройте и нарисуйте график функции распределения вероятностей.

22.Задана функция плотности случайной величины, распределенной по нормальному закону: .Определите математическое ожидание.

23.Запишите выражение функции плотности распределения вероятностей для нормально распределённой случайной величины, если ее математическое ожидание М(х) = 0, а дисперсия D(х) = 4.

24.Случайная величина принимает значения: -0,1; 0; 0,1; 0,3; с равными вероятностями. Найдите математическое ожидание и дисперсию.

25.Автомат изготавливает шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная ее величина Х распределена по нормальному закону со средним квадратическим отклонением σ = 0,4 мм, Найдите, сколько будет годных шариков среди ста изготовленных.

26.Случайная величина принимает два значения: 0 и 1. Найдите вероятность того, что появится значение Х=0, если вероятность значения Х=1 равна 0,2.

27. Задана функция плотности случайной величины, распределенной по нормальному закону: . Определите вероятность Р (Х > 5 ).

28.Может ли при каком-либо значении аргумента функция распределения вероятностей быть больше 1?

29.Случайная величина распределена по нормальному закону с математическим ожиданием М(х) = 2. Найдите вероятность Р (х>3), если вероятность Р (х<1) = 0,375.

30.Случайная величина принимает два значения: 0 и 1. Вероятность значения Х=1 равна 0,1. Определите математическое ожидание.

31.Задана функция плотности вероятности случайной величины, распределенной по нормальному закону: .Определите математическое ожидание.

32. Может ли при каком-либо значении аргумента функция распределения вероятностей быть меньше единицы?

33. Случайная величина распределена по нормальному закону с математическим ожиданием M(x) = 2. Найдите вероятность Р(х > 2), если вероятность Р(х < 1) = 0,375.

34.Случайная величина принимает два значения: 0 и 1. Вероятность того, что появится значение х = 0, равна 0,2. Определите дисперсию.

35. Задана функция плотности вероятности случайной величины, распределенной по нормальному закону: . Определите дисперсию.

36. Может ли при каком-либо значении аргумента функцияраспределения вероятностей быть отрицательной?

37. Случайная величина распределена по нормальному закону с математическим ожиданием M(x) = 2. Найдите вероятность Р(х < 2), если вероятность Р(х < 1) = 0,375.

38. Случайная величина принимает шесть значений: 0, 1, 2, 3, 4, 5 с равными вероятностями. Определите математическое ожидание.

39. Задана функция плотности вероятности случайной величины, распределенной по нормальному закону: . Определите дисперсию.

40.Может ли при каком-либо значении аргумента функцияраспределения вероятностей бытьменьше единицы?

41.Случайная величина распределена по нормальному закону с математическим ожиданием M(x) = 2. Найдите вероятность Р(х > 3), если вероятность Р(х < 1) = 0,375.

42. Случайная величина принимает пять значений: 1, 2, 3, 4, 5 с равными вероятностями. Определите стандартное отклонение.

43.Случайная величина распределена по нормальному закону с математическим ожиданием M(x)=2. Найдите вероятность P(1
44. Случайная величина задана законом распределения в виде таблицы:

х	-1	0	2	2,5
р	0,2	0,3	0,4	0,1

Определите математическое ожидание.

45. Дискретная случайная величина х принимает 3 возможных значения : с вероятностью ; с вероятностью и с вероятностью . Найдите и , зная, что М(х) = 8.

46.Случайная величина задана таблицей:

Х	-2	-1	0	1	2
Р	0,05	0,15	0,1	0,5	0,2

постройте и нарисуйте график распределения вероятностей.

47.Случайная величина распределена по нормальному закону с математическим ожиданием M(x)=0. Определить вероятность того, что она примет значения x < 0, если известно, что вероятность принять значения из промежутка -2 < x < 2 равна 0,8.