Главная страница
Навигация по странице:

  • Содержание отчёта

  • Пример и методические указания Составим программу вычислений в Mathcad с пояснениями.1.

    		•

    ТАУ. Задание 1. Mathcad Передаточная, переходная и весовая функции систем автоматического управления


    Скачать 133.5 Kb.
    НазваниеMathcad Передаточная, переходная и весовая функции систем автоматического управления
    Дата19.12.2021
    Размер133.5 Kb.
    Формат файлаdoc
    Имя файлаЗадание 1.doc
    ТипДокументы
    #308997

    ЗАДАНИЕ 1

    (выполняется в программе Mathcad)

    Передаточная, переходная и весовая функции систем автоматического управления
    Для выполнения этого задания следует знать:

    1. Основные понятия и классификация систем автоматического управления (САУ).

    2. Математическое описание линейных САУ. Одностороннее преобразование Лапласа.

    3. Свойства одностороннего преобразования Лапласа. Передаточные функции.

    4. Временные характеристики САУ. Нахождение временных характеристик линейных систем по передаточным функциям.




    1. Передаточная функция системы автоматического управления задана выражением вида: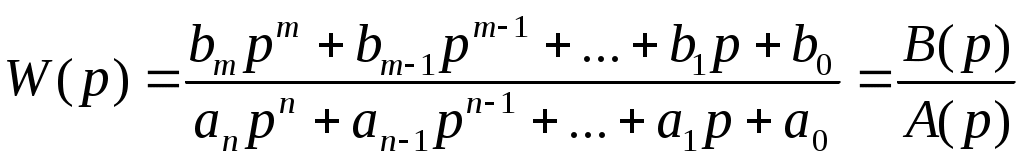


    , где m ≤ n.


    Коэффициенты ai и bi приведены в таблице 1.1. Найти полюсы и нули передаточной функции и построить корневой годограф. На корневом годографе обозначить полюсы одним цветом (или отметками), а нули – другим.
    Таблица 1.1

    V
    a5
    a4
    a3
    a2
    a1
    a0
    b5
    b4
    b3
    b2
    b1
    b0

    1
    7,6
    11,1
    –
    3,5
    –
    18
    17,9
    –
    24
    6,9
    13,3
    –

    2
    0,6
    1,1
    –
    –
    4,4
    0,3
    –
    27,1
    19,9
    –
    4,2
    15

    3
    –
    4,4
    –
    6,8
    7,4
    16
    –
    –
    –
    –
    38,3
    14,5

    4
    10,5
    –
    3,9
    8
    –
    5,3
    –
    –
    –
    1,6
    0,7
    –

    5
    –
    11
    6,2
    16,2
    5,7
    –
    –
    4,7
    23,2
    –
    26,8
    32,4

    6
    14,9
    7,2
    4,6
    21,7
    10,8
    1,6
    –
    –
    –
    –
    –
    15,3

    7
    –
    1,9
    17,8
    2,9
    18,6
    –
    –
    –
    20,4
    0,3
    17,1
    18,5

    8
    6,7
    8
    18,9
    –
    –
    5,2
    30
    22,4
    –
    34,3
    –
    30

    9
    10,5
    8
    –
    13,7
    8,7
    –
    10,2
    –
    22,1
    20,9
    –
    –

    10
    –
    0,5
    –
    0,1
    1,6
    7,1
    –
    –
    –
    2,1
    –
    27,2

    11
    16,2
    –
    –
    2,9
    14,6
    0,6
    6,2
    26,8
    –
    –
    39,3
    11,8

    12
    –
    1,7
    19
    5,5
    19,6
    –
    –
    32,6
    5,7
    12,3
    –
    –




    1. Найти переходную h(t) и весовую w(t) функции системы с учётом того, что

    , .

    При этом оригиналы h(t) и w(t) найти с помощью теоремы разложения: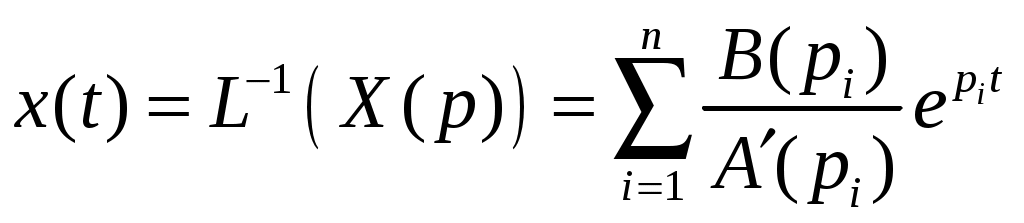

    ,

    где pi – i-й корень уравнения .

    Если среди корней какого-либо из уравнений или (или обоих) имеются кратные, выражение для нахождения оригинала по теореме разложения будет сложным. Поэтому соответствующие оригиналы следует найти в Mathcad с помощью встроенного обратного преобразования Лапласа (ключевое слово invlaplace).

    1. Построить графики функций h(t) и w(t). Интервал времени подобрать для наглядного отображения процесса.


    Содержание отчёта (оформляется в MS Word):

      • титульный лист;

      • задание по варианту;

      • передаточная функция системы по варианту;

      • нахождение весовой и переходной функций;

      • графики переходной и весовой функций, построенные в одном масштабе по оси времени.



    Пример и методические указания

    Составим программу вычислений в Mathcad с пояснениями.

    1.

    Пусть заданы коэффициенты многочленов A(p) и B(p):





    Определим многочлены A(p) и B(p) с учётом коэффициентов и передаточную функцию: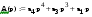







    Для нахождения корней уравнений A(p)=0 и B(p)=0 выразим коэффициенты многочленов в виде столбцов с помощью ключевого слова coeffs (с панели символьных операций). Коэффициенты в столбцах расположатся по возрастанию степени.



    Найдём нули и полюсы передаточной функции с помощью функции polyroots().

    Функция имеет аргументом столбец коэффициентов и возвращает вектор-столбец корней:





    На корневом годографе изобразим мнимые части корней относительно действительных. Обозначим нули и полюсы разными символами (в контекстном меню графика – пункт «Формат»):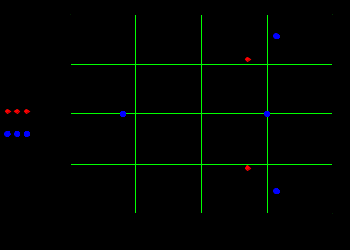



    2.

    Чтобы найти весовую функцию системы по формуле w(p)=L-1(W(p)), определим функцию производной знаменателя A1(p):



    По теореме разложения найдём оригинал, где n-число полюсов (число столбцов в матрице pA):





    3.

    Для построения графика функции зададим шаг и временной интервал:





    Отобразим график функции w(t):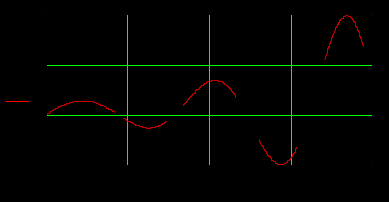



    Из-за погрешностей вычисления функция w(t) в некоторых точках имеет комплексное значение с исчезающе малой мнимой частью, например:



    Поэтому для корректного отображения весовой функции используем только её действительную часть: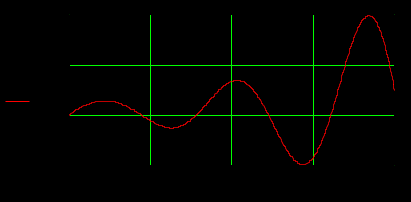



    Аналогично, чтобы найти переходную функцию системы по формуле h(p)=L‑1(W(p)/p), определим функцию производной знаменателя A2(p):



    Очевидно, что корни многочлена знаменателя p∙A(p) будут такими же, как и многочлена A(p), но с добавкой одного нулевого корня:







    Здесь образовались два нулевых корня (нулевой корень кратности 2). В этом случае необходимо применить теорему разложения в общем виде (для случая кратных корней) или, что проще, использовать возможности Mathcad для нахождения оригинала с помощью обратного преобразования Лапласа.

    Числа в выражении округлены с помощью ключевого слова float до четырёх значащих цифр.



    Отобразим график полученной переходной функции: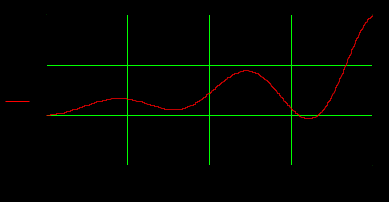

    написать администратору сайта