Ответы на вопросы к экзамену дисциплина Алгебра и геометрия. алгебра. Вопросы к экзамену по дисциплине Алгебра и геометрия 1 Числа. Числовые поля (Q, R, С). Поле комплексных чисел

• Название: Вопросы к экзамену по дисциплине Алгебра и геометрия 1 Числа. Числовые поля (Q, R, С). Поле комплексных чисел
• Анкор: Ответы на вопросы к экзамену дисциплина Алгебра и геометрия
• Дата: 19.03.2022
• Размер: 0.63 Mb.
• Имя файла: алгебра.docx
• Тип: Вопросы к экзамену; #404373

Вопросы к экзамену по дисциплине Алгебра и геометрия

1 Числа. Числовые поля (Q, R, С). Поле комплексных чисел.

R-множество действительных чисел. , которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.

Q-рациональные числа. , которые можно представить в виде положи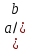тельной обыкновенной дроби , отрицательной обыкновенной дроби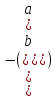 или числа ноль.

C-комплексные числа. это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i² = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi.

Комплексное число равно нулю, если соответственно равны нулю его действительная и мнимая части

2 Алгебраическая, тригонометрическая и показательная форма комплексного числа. Действия с комплексными числами. Формулы Муавра.

Комплексные числа: Z=x+i*y, где x–действительная часть, i-мнимая единица (i²=-1), y-мнимая часть,

Алгебраическая форма:z = a + bi,

Тригонометрическая форма: z = r(cos  +isin )

Показательная форма: z = re^iφ

Три формы представления комплексного числа.

1. Представление комплексного числа в виде z = x +iy называется алгебраической формой.

2. Из справедливости равенств (1.1.2) следует, что комплексное число можно представить в тригонометрической форме z = r(cos+isin) (1.1.4)

3. Из справедливости формулы Эйлера cos i+sin i = e следует представление комплексного числа в показательной форме

Действия с комплексными числами

1) Сложение и вычитание

2) Умножение.

3) Деление.

4) Возведение в целую положительную степень.

5) Извлечение корня. если z=r(cos +isin) комплексное число, то существует ровно n различных значений корня степени n, определяемых формулами Муавра: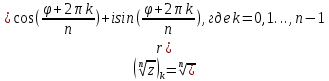

z^n = r^n ( cos n φ+ i sin n φ) формула муавра

где n – целое положительное число. Это выражение называется формулой Муавра. (Абрахам де Муавр (1667 – 1754) – английский математик). Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.

3 Матрицы и определители.

Матрица А размера mn – совокупность чисел, расположенных в виде таблицы из m строк и n столбцов.

Числа a_ij, входящие в состав матрицы, называют ее элементами.

Квадратная матрица – матрица, где число строк m равно числу столбцов n, т. е. m=n.

Диагональная матрица – матрица, где все элементы, кроме главной диагонали равны нулю.

Единичная матрица – матрица, где все элементы, главной диагонали равны единицы.

Нулевая матрица – матрица, где все элементы равны нуля.

Треугольная матрица – матрица, где все элементы равные нулю, расположены выше (ниже) главной диагонали.

Матрица-строка (столбец) – матрица, состоящая из одной строки (столбца).

Две матрицы A и B называются равными (A=B), если они одинаковых размеров, и все их соответствующие элементы равны (т. е. элементы, стоящие на одинаковых местах, равны).

Матрица А^Т называется транспонированной по отношению к матрице A, если она получена из матрицы A заменой строк столбцами, а столбцов строками с сохранением их номеров.

Определитель квадратной матрицы A n-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Определителем квадратной матрицы А второго порядка, называется число, равное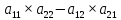

Определитель - это скалярная величина, которая может быть вычислена и поставлена в однозначное соответствие любой квадратной матрице. Число, определяющее свойство квадратной матрицы (детерминант)
4 Свойства определителей. Вычисление определителей.

Вычисление определителей.

Определителем квадратной матрицы А второго порядка, называется число, равное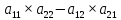

Определитель квадратной матрицы A n-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Свойства определителей:

1. величина определителя не изменится при транспонировании.

2. определитель, все элементы некоторой строки (столбца) которого равны нулю, равен нулю.

3. величина определителя при перестановке любых двух строк (столбцов) меняет знак на противоположный.

4. общий множитель некоторой строки (столбца) можно выносить за знак определителя.

5. если элементы какой-либо строки (столбца) представляются в виде суммы двух слагаемых, то определитель может быть разложен на сумму двух определителей, в первом из которых элементы названной строки (столбца) равны первым слагаемым, во втором - вторым.

6. величина определителя не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на одно и тоже число. свойства определителей используются при вычислении определителей (в особенности свойство 6).

5 Системы линейных алгебраических уравнении. Формулы Крамера.

Алгебраическое уравнение относительно неизвестных x называется линейным, если его можно записать в виде системы с постоянными числами (коэффициентами уравнения) и называемое свободным членом. Совокупность m линейных алгебраических уравнений относительно неизвестных, рассматриваемых совместно называются системой линейных алгебраических уравнений (СЛАУ).

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения. Совместная система называется определенной, если она имеет одно решение, и неопределенной, если она имеет более одного решения. Две СЛАУ с одним и тем же числом неизвестных называются эквивалентными или равносильными, если они обе несовместны или обе совместны и имеют одни и те же решения. Число уравнений в эквивалентных системах может быть различным.

Матрица, составленная из коэффициентов при неизвестных, называется матрицей системы. Матрица системы с добавлением столбцов правых частей называется расширенной матрицей системы

Если определитель системы отличен от нуля, то система совместна и имеет единственное решение, которое находится по формулам Крамера:

6 Действия над матрицами: сложение и умножение матриц.

Сложение матриц. Суммой двух матриц A и B размера mn называется матрица C=A+B такого же размера, каждый элемент которой C = a_ij+b_ij равен сумме элементов матриц A и B, стоящих на тех же местах.

Сложение матриц обладает следующими свойствами:

1) A+B=B+A коммутативность;

2) (A+B)+C=A+(B+C) ассоциативность;

3) A +  =  +А=А

Умножение матрицы на число. Для того, чтобы умножить матрицу A на число α, нужно каждый элемент этой матрицы умножить на это число. В результате получится матица С= A   .

Умножение матриц удовлетворяет следующим свойствам:

1) Определитель квадратной матрицы порядка n, равной произведению матрицы на число, равен произведению определителя матрицы на это число в степени n;

2) дистрибутивность: (A+B) = A  + B  ;

3) распределительный закон: A(α+β) = A  + A  β;

4) A(αβ)= (Aβ);

5) A+(-A) = (-A) +А=0;

Умножение матриц.

Произведением строки a на столбец b называется число, равное сумме произведений элементов строки и столбца с одинаковыми номерами

Длина строки (число столбцов) матрицы A должны совпадать с высотой строки (количеством строк) матрицы B.

Произведением матрицы A на матрицу B называется матрица C размера m p  , каждый элемент которой, стоящий в строке с номером i и столбце с номером j равен произведению i -той строки матрицы A на j-тый столбец матрицы B.

Умножение матриц обладает следующими свойствами:

1)Если обе матрицы A и B квадратные, то определены два произведения AB и BA, но ABBA. Если матрицы A и B таковы, что выполняется AB=BA, то они называются перестановочными);

2) A = ,   A =  для любой матрицы A, если оба произведения матриц определены

3) ассоциативность: (AB) C= A(B C);

4) дистрибутивность: A(B+C) = AB+ AC;

5) (AB) = ( A)B);

6)Если определено произведение AB , то определено произведение BTAT , причем (AB)T= BTAT

7)Если матрицы A и B квадратные, то определитель их произведения равен произведению определителей матриц

7 Обратная матрица. Решение систем матричным способом.

Квадратная матрица B, удовлетворяющая равенствам AB= BA=E, где E – единичная матрица того же порядка, что A и B, называется обратной к A и обозначается A −1.

Вообще, матрица, определитель которой отличен от нуля, называется невырожденной. В противном случае матрицу называют вырожденной.

Для того чтобы найти обратную матрицу к матрице A, следует:

1) Найти определитель матрицы A, убедиться, что ΔA0;

2) Найти алгебраические дополнения Aij ко всем элементам матрицы A;

3) Из полученных чисел составить матрицу, ее называют матрицей, союзной к матрице A;

4) Полученную матрицу транспонируем;

5) Транспонированную матрицу умножаем на число

Свойства обратной матрицы:

1. (AB)^-1=B^-1A^-1

2. |A^-1 |=|A|^-1

3. (A^-1) ^-1=A

4. (A^T) ^-1=(A^-1)^T

Если матрица A невырожденная, то существует обратная матрица A-1. Тогда умножив обе части уравнения (слева на обратную матрицу, мы получим решение системы: X=A-1B

Матрица А* называется союзной к матрице А, если она составлена из алгебраических дополнений элементов матрицы А и транспонирована

Матрица А⁻1 называется обратной к матрице А, если выполняется условии: А* А⁻1= А⁻1* А=E

Всякая невырожденная матрица имеет обратную: А⁻1=А*/ΔА

8 Ранг матрицы. Методы нахождения ранга.

Рангом матрицы называется наибольший из порядков миноров, отличных от нуля Свойства:

1) при транспонировании ранг не меняется.

2)Если из матрицы вычеркнуть нулевую строчку, то ранг не изменится.

3)При элементарных преобразованиях ранг не меняется

1. Метод окаймления миноров. Он состоит в следующем:

a) Находится минор рассматриваемой матрицы, отличный от нуля (первого, второго и т.д. порядков).

б) Окаймляя его строками и столбцами (из числа оставшихся строк и столбцов), находят минор следующего порядка, отличный от нуля. Как только такой минор нашелся, прекращают вычисление минора данного порядка и переходят к вычислению миноров следующего порядка, получаемых окаймлением найденного. Процесс продолжается до тех пор, пока не получат, что все миноры какого-либо порядка равны нулю. Миноры более высоких порядков уже не рассматриваются.

2. Метод элементарных преобразований. Он заключается в том, что элементарными преобразованиями исходная матрица приводится к ступенчатому виду:

9 Теорема о базисном миноре.

Любой, отличный от нуля, минор матрицы А порядка, равного рангу матрицы, называется базисным минором. Столбцы и строки, на пересечении которых расположен базисный минор, называются базисными столбцами и строками. Теорема 1.9.1. (о базисном миноре). Всякий столбец (строка) матрицы является линейной комбинацией её базисных столбцов (строк). Сами базисные столбцы (строки) линейно независимы.

10 Теорема Кронекера-Капелли.

Теорема 1.10.1. (Кронекера-Капелли) Для того чтобы СЛАУ (1.10.1) была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.

11 Однородные системы уравнений. Фундаментальная система решений. Общее решение однородной системы.

Однородные СЛАУ всегда имеют нулевое (тривиальное) решение.

Если RgA=n, то однородная система имеет только тривиальное решение X = (0,..., 0) .

Если RgA=rn, то система имеет n-r линейно независимых решений.

Совокупность решений называют нормальной фундаментальной системой решений. Вообще любая система линейно независимых решений называется фундаментальной системой решений.

Выражение вида X=C₁X₁+C₂X₂+…+ Cn-rX_n-r, называют общим решением однородной системы уравнений.

12 Общее решение неоднородной системы. Метод Гаусса.

Метод Гаусса: Будем полагать что в системе n-уравнений…

Как правило в методе Гаусса система 1 представляется в форме расширенной матрицы. Очевидно что элементарные преобразования над строками расширенной матрицы соответствуют аналогичным преобразованиям системы. При этом система преобразуется в эквивалентную.

Метод Гаусса состоит из 2ух этапов: 1-прямой ход , система с помощью элементарных преобразований над строками приводится к ступенчатому виду (под главной диагональю нули, на главной диагонали единицы). 2этап: обратный ход,из последнего уравнения находим неизвестную и подставляем ее в вышестоящее ур-е. и т.д.

13 Системы координат. Векторы. Линейные операции над векторами. Проекция вектора на ось. Направляющие косинусы и длина вектора.

Система координат это совокупность точки начала отсчёта (нач.координат) и некоторого базиса.Как на плоскости так и в пространстве возможно задание самых разнообразных систем координат. Декартова система координат

Вектор-направленный отрезок. Проекция вектора М на ось L – это основание перпендикулярное MM1 опущенного на ось L. Если угол между вектором и осью острый то проекция будет с плюсом, если угол тупой то с минусом.

14 Линейные пространства. Линейная зависимость и независимость.

Множество всех прямоугольных матриц размерности m  n; множество всех n-мерных векторов, множество решений системы линейных однородных уравнений образуют линейные пространства.

Система векторов называется линейно зависимой, если существуют такие числа не все равные нулю, что их линейная комбинация с этими коэффициентами равна нулевому вектору; линейно независимой, если последнее равенство возможно тогда и только тогда, когда все равны нулю.

15 Базис. Координаты. Размерность.

Любая совокупность (подсистема) векторов из системы векторов называется базисом данной системы если:

1) векторы этой совокупности (подсистемы) линейно независимы;

2) любой вектор системы является линейной комбинацией векторов этой подсистемы

3)каждый вектор хL представляет собой линейную комбинацию векторов этой системы, т.е

Коэффициенты этого разложения называют координатами вектора x по базису. Количество векторов базиса называют размерностью линейного пространства.

16 Скалярное произведение векторов.

Скалярное произведение векторов называют число, равное произведению длин этих векторов на косинус угла между ними. ,

Свойства скалярного произведения:

1. 
   ;
   
2. 
   ;
   
3. 
   ;
   
4. 
   ;
   
5. 
   , m=const.
   

Угол между векторами:

17 Ориентация тройки векторов. Векторное произведение векторов.

Упорядоченная тройка векторов называется правой (положительно ориентированной), если из конца третьего вектора поворот от вектора к вектору по наименьшему углу происходит против часовой стрелки), и левой (отрицательно ориентированной) – если поворот по наименьшему углу происходит по ходу часовой стрелки

Векторным произведением векторов( , ) называется вектор , удовлетворяющий следующим условиям:

1) , где  - угол между векторами , sin  0; 0   

2) вектор c  ортогонален векторам

3) образуют правую тройку векторов.

Свойства векторного произведения векторов:

1. 
   ;
   
2. 
   если  или = 0 или = 0;
   
3. 
   ;
   
4. 
   ;
   
5. 
   ;
   
6. 
   Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах .
   

18 Смешанное произведение векторов.

Смешанным произведением векторов называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов .

Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах .

Свойства смешанного произведения:

1. 
   Смешанное произведение равно нулю, если:
   

а) хоть один из векторов равен нулю;

б) два из векторов коллинеарные;

в) векторы компланарны.

2. 
   ;
   
3. 
   
   
4. 
   =
   
5. 
   Объем треугольной пирамиды, образованной векторами , равен
   
6. 
   ;
   

19 Уравнения линий на плоскости.

Ф(х,у) =0,называется уравнением линии L, если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты ни одной точки, не лежащей на линии L.

20 Уравнения прямой на плоскости (общее, с угловым коэффициентом, в отрезках, нормальное).

Общие уравнение прямой: Ах + Ву + С = 0

С угловым коэффициентом: у = kx + b

В отрезках:

Нормальное:

21 Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости. Пучок прямых.

Угол между прямыми:

Расстояние от точки до прямой: Пучок прямых: y-y₀=k(x-x₀₎
22 Уравнения плоскости. Расстояние от точки до плоскости. Пучок плоскостей.

Уравнения плоскости: Ax + By + Cz + D = 0

Расстояние от точки до плоскости:

Пучок плоскостей:

23 Прямая в пространстве. Точка пересечения прямой и плоскости.

Каноническими уравнениями прямой в пространстве:

24 Кривые 2-го порядка (эллипс).







25 Кривые 2-го порядка (гипербола).






26 Кривые 2-го порядка (парабола).





27 Цилиндры 2-го порядка.





28 Эллипсоид.



29 Однополостный гиперболоид.



30 Двуполостный гиперболоид.



31 Эллиптический параболоид.



32 Гиперболический параболоид.



33 Конус.





34. Понятие линейного пространства и линейного оператора. Базис и размерность.

Пусть V - непустое множество элементов x, y, z, ... и R - множество действительных чисел. Пусть на множестве V заданы операция сложения, которая каждой паре x, y элементов V ставит в соответствие определённый элемент z множества V, и операция умножения элементов V на число, которая каждому элементу множества V и произвольному числу  множества R ставит в соответствие определённый элемент z множества V. Элемент z называют соответственно суммой и произведением числа  на элемент множества V и пишут z = x + y и z =  x или z= x  .

Если для операции сложения и умножения на число выполняются аксиомы:

1. x + y = y + x,  x, y  V

2. (x + y) + z = x + (y + z),  x, y, z  V

3.  0  x {x+ 0 = x}. 0 называется нулевым элементом множества V.

4.  x  (- x) {x + (- x) = 0}. Элемент (- x) называется противоположным элементу x.

5. 1  x =x,  x  V

6.  (  x)=(  )x,    , R,  x  V

7.  (x + y) =  x+  y,   R,  x, y  V

8. (  +  )x =  x +  x,    , R,  x  V

то непустое множество V называется вещественным линейным пространством. Элементы x, y, z, ...,  V называются элементами пространства или векторами.

Пусть V и W - линейные пространства размерностей n и m. Оператором А, действующим из V в W (А: V → W) называется отображение V в W, сопоставляющее каждому элементу x  V некоторый элемент y  W. Записывается y = A(x) или y = Аx. Элемент x  V называется прообразом y, y - образом x. Оператор А: V → W называется линейным, если  x1, x2  V и для любого  R выполняются соотношения: 1. А(x1 + x2)=Аx1 + Аx2 - свойство аддитивности оператора; 2. А(  x)=  Аx. - свойство однородности оператора.

35. Матрица линейного оператора. Невырожденные линейные операторы. Примеры.

П усть е₁, е₂, …, е_n - некоторый базис в пространстве V и А - линейное преобразование в V. Для любых n векторов g₁ g₂ ,..., gn существует одно и только одно линейное преобразование А, такое, что Ае₁=g₁, Ае₂=g₂, ..., Ае_n=g_n. Обозначим координаты вектора g_k в базисе e₁ e₂, ..., e_n через 1 2 , a₁, a₂, ..., a_n , т.е. положим . Совокупность чисел a_ik (i, k=1,2, ..., n) образует матрицу А=( ik a ), которую мы назовём матрицей линейного преобразования в базисе e₁ e₂, ..., e_n , т.е.

36. Действия с линейными операторами.

Пусть А  и В – два линейных оператора, действующих из V в W. Суммой этих операторов назовем оператор А + В, определяемый равенством (А + В) А +В  для любого   из V. Легко видеть, что сумма линейных операторов тоже будет линейным оператором.

Сложение линейных операторов обладает, очевидно, следующими свойствами:

1. А + В = В +А.

2. (А +В) +Е = А + (В + Е).

3. А + О = А  для любого А.

4. (–А) + А = О.

Произведением  линейного  оператора  на  скаляр  α  назовем оператор αА, определяемый равенством  А) А . Ясно, что αА – тоже линейный оператор.

Для умножения линейного оператора на число справедливы, очевидно, следующие свойства:

1. А = А; 0А = О; (–1)А= –А.

2. α (βА)  А.

3.  А =  А + βА.

4.  (А + В) =  А +  В.

Обозначим через   множество всех линейных операторов, действующих из V в W.

Произведением линейных операторов А и В из   называется оператор АВ, определяемый следующим образом: (А В) А(В  для любого   из V. Произведение линейных операторов тоже будет линейным оператором.

Справедливы следующие свойства умножения линейных операторов:

1.  АВ) = ( А )В.

2. (АВ)Е = А (ВЕ).

3. (А + В)Е = АЕ + ВЕ,  Е(А + В) = ЕА + ЕВ.

37. Изменение матрицы оператора при переходе к новому базису.

При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве X произошел переход от базиса e = {e 1, ..., e n} к базису e' = {e' 1, ..., e' n}. Связь между матрицей A e оператора A в базисе e и матрицей A e' этого оператора в базисе e' задается формулой.

38. Образ и ядро линейного оператора.

Пусть A – линейный оператор, действующий в линейном пространстве V. Совокупность векторов y = Ax, где x  V , называется образом оператора A и обозначается . Множество всех векторов x V , для которых Ax = 0 , называется ядром оператора A и обозначается . Образ и ядро линейного оператора A являются подпространствами линейного пространства V

39. Ранг и дефект линейного оператора. Примеры.

Размерность образа оператора A совпадает с рангом матрицы линейного оператора и называется рангом оператора. Действительно, образ оператора A порождается векторами Af1 ¸Af2 ,..., Afn , где f1 f2 ,..., fn - какой-нибудь базис пространства V, и значит, его размерность равна максимальному числу линейно независимых векторов в системе Af1 ¸Af2 ,..., Afn, или максимальному числу линейно независимых столбцов матрицы. Размерность ядра линейного оператора называют его дефектом.

Найти образ, ядро, ранг и дефект линейного оператора A, имеющего в базисе матрицу

40. Невырожденные операторы и их свойства.

1) Невырожденный оператор A имеет невырожденный обратный оператор A-1 , такой что , где I - тождественный оператор, действующий по правилу Ix x = для любого x V .

2) Образ невырожденного линейного оператора, заданного в линейном пространстве V, совпадает со всем пространством V. ImA V= .

3) Ядро невырожденного оператора состоит только из нулевого вектора KerA = 0.

4) Ранг невырожденного оператора равен размерности линейного пространства, в котором он определен.

5) Дефект невырожденного оператора равен нулю.

6) Если операторы A и B, определенные в линейном пространстве V, невырожденные, то их произведение оператор C A B =  тоже невырожденный.

7) Невырожденный оператор, действующий в линейном пространстве V, осуществляет взаимно однозначное отображение этого пространства.

8) Невырожденный оператор осуществляет преобразование любой линейно независимой системы векторов опять в линейно независимую.

41. Собственные значения и собственные векторы линейного оператора. Линейная независимость собственных векторов, отвечающих различным собственным числам. Диагональный вид матрицы.

Собственным вектором линейного преобразования А (квадратной матрицы А) называется такой ненулевой вектор X, который удовлетворяет уравнению AX = X, где  - число

собственный вектор – это такой вектор, который под действием линейного оператора переходит в коллинеарный вектор, т.е. просто умножается на некоторое число. В отличие от него, несобственные векторы преобразуются более сложно.

Теорема 5.8.2. Собственные векторы линейного оператора, отвечающие попарно различным собственным значениям, являются линейно независимыми.

Квадратная матрица называется диагональной, если все ее элементы, отличные от нуля, расположены на главной диагонали.

42. Независимость характеристического многочлена от выбора базиса. Теорема Кели-Гамильтона.

Теорема 5.8.1. Характеристический многочлен линейного оператора не зависит от выбора базиса.

Теорема 5.7.1. (Кели-Гамильтона). Матрица линейного оператора является корнем своего характеристического многочлена.

43. Подобные матрицы.

Определение. Две квадратные матрицы порядка п А и В называются подобными, обозначение A B , если найдется невырожденная квадратная матрица Р порядка п такая, что В=Р^-1АР.

Ясно, что матрицы одного и того же линейного оператора в разных базисах подобны.

Свойства подобных матриц.

Теорема. Отношение подобия квадратных матриц порядка n рефлексивно, симметрично и транзитивно. Это значит, что для любых квадратных матриц А, В и С(а) A  A;(б) A B B A;(в) A B, B C  A  C,

44. Необходимые и достаточные условия диагонализируемости оператора.

Линейный оператор A, определенный в n-мерном линейном пространстве L n называется диагонализируемым, если в этом пространстве существует базис, в котором матрица оператора имеет диагональный вид. В частности, если все собственные значения линейного оператора – попарно различные действительные числа, то оператор является диагонализируемым. Действительно, согласно теореме 5.8.2, соответствующие им собственные векторы являются линейно независимыми, а значит, образуют базис линейного пространства.

Пример 5.9.1. Выяснить, является ли диагонализируемым линейный оператор, заданный в некотором базисе матрицей A. В случае, если оператор диагонализируемый, построить диагональный вид его матрицы и указать соответствующий базис.

45. Определение евклидова пространства. Ортонормированная система векторов. Метод ортогонализации Шмидта.

Пусть E —линейное пространство над полем вещественных чисел. Скалярным произведением на E будем называть произвольную функцию, ставящую в соответствие упорядоченной паре векторов x,y ∈ E вещественное число (x,y) и обладающую следующими свойствами:

1) симметричность (коммутативность): ∀x,y ∈ E (x,y)=(y,x); 2) дистрибутивность: ∀x,y,z ∈ E (x+y,z)=(x,z)+(y,z),

3) линейность: ∀x,y,∈ E , ∀α ∈ R (αx,y)=α(x,y); 4) положительность: ∀x ≠ 0 (x,x) > 0.

Евклидово линейное пространство (ЕЛП) — это линейное пространство над R, на котором зафиксировано некоторое скалярное произведение.

Система векторов e1,e2,…,en называется ортонормированной, если векторы этой системы попарно ортогональны друг другу, и длина каждого вектора равна единице, т.е.

Теорема 5.10.2. Векторы, образующие ортонормированную систему, являются линейно независимыми.

Пусть в линейном евклидовом пространстве имеется линейно независимая система векторов f1, f2,…,fn . Из нее всегда можно построить ортонормированную систему с помощью алгоритма ортогонализации Шмидта.

46. Сопряженные и самосопряженные операторы, их свойства.

Линейный оператор A* , действующий в линейном евклидовом пространстве E, называется сопряженным к линейному оператору A, действующему в том же пространстве, если для любых двух векторов x,y  E , выполняется равенство ( Ax ,y) = (x ,A* y ).

Линейный оператор A, действующий в евклидовом пространстве, называется самосопряженным, если он совпадает с сопряженным, т.е. * A A = . Это означает, что для любых двух векторов x,y E , выполняется равенство ( Ax ,y) = (x ,A y ).

Свойства сопряженного оператора:

1. (αA) ∗ = αA ∗ , α ∈ R. 2. (A ∗ ) ∗ = A. 3. (A + B) ∗ = A ∗ + B ∗ . 4. (AB) ∗ = B ∗A ∗ . 5. Если линейный оператор A невырожден, то сопряженный с ним оператор A ∗ также невырожден и выполняется равенство

Свойства самосопряженного оператора:

1. Для того, чтобы линейный оператор A был самосопряженным необходимо и достаточно, чтобы его матрица A в каком-либо ортонормированном базисе была симметрической, т.е. A = AT .

2. Характеристическое уравнение самосопряженного оператора имеет только действительные корни.

3. Собственные векторы самосопряженного оператора A, отвечающие разным собственным значениям, ортогональны.

4. Пусть A - самосопряженный оператор n-мерного евклидова пространства E и λ1, . . . , λn – попарно различные собственные значения этого оператора. Тогда в E существует ортонормированный базис, в котором матрица этого линейного оператора имеет диагональный вид, а диагональные элементы такой матрицы – собственные значения.

5. Для любого самосопряженного оператора A существует ортонормированный базис, состоящий из собственных векторов оператора A. Матрица линейного оператора A в этом базисе имеет диагональный вид, на диагонали расположены собственные значения оператора A, повторяющиеся столько раз, какова их кратность.

6. Если A – симметрическая матрица порядка n, то существует такая невырожденная матрица T порядка n, что T −1AT – диагональная матрица с диагональными элементами в виде собственных значений λ1, . . . , λn матрицы A самосопряженного оператора A.

47. Ортогональные операторы и ортогональные матрицы.

Линейный оператор A евклидова пространства E называется ортогональным оператором, если он сохраняет скалярное произведение в E, т.е. для любых двух векторов x,y E выполняется ( Ax,Ay,) = ( x,y).

Ортогональному оператору в любом ортонормированном базисе соответствует ортогональная матрица. Если матрица, транспонированная к невырожденной матрице P, совпадает с матрицей, обратной к ней, P^T = P^-1 , то такая матрица называется ортогональной.

48. Квадратичные формы. Матрица квадратичной формы. Канонический вид квадратичной формы.

Квадратичной формой от переменных x1,x2,…,xn называется однородный многочлен второй степени от этих переменных. В общем виде квадратичную форму можно записать в виде F= aijxixj. Из коэффициентов aij можно составить симметрическую матрицу A=aiji,j=1,…n, это матрица квадратичной формы.

Квадратичная форма имеет канонический вид F=1y12+2y22+…+ nyn2, если ее матрица является диагональной, т. е. форма содержит лишь слагаемые с квадратами переменных. Здесь y1,y2,…,yn - переменные, связанные с исходными переменными x1,x2,…,xn невырожденным линейным преобразованием

49. Приведение квадратичной формы к каноническому виду методом Лагранжа. Примеры.

Элементарным способом приведения квадратичной формы к каноническому виду является метод Лагранжа.

Идея метода Лагранжа состоит в том, что прием, используемый в п.2 (выделение полного квадрата), исключает одну переменную из числа ведущих. Например, если переменная x1 — ведущая (т.е. и хотя бы один из коэффициентов отличен от нуля), то выделяем полный квадрат по переменной  (собираем все члены с и дополняем их сумму до полного квадрата):

50. Приведение квадратичной формы к каноническому виду ортогональным преобразованием.

Существует довольно простой метод (метод Лагранжа) приведения квадратичной формы к каноническому виду. Этот метод, однако, во многих задачах не дает нужного результата. Например, в задачах аналитической геометрии часто требуется привести общее уравнение кривой или поверхности второго порядка к каноническому виду, причем такое приведение требуется осуществить с помощью весьма специального преобразования переменных (а именно ортогонального); метод Лагранжа не всегда обеспечивает это условие. В связи с этим мы укажем способ, основанный на отыскании собственных значений матрицы квадратичной формы. Теорема 38. Всякая квадратичная форма с матрицей А может быть приведена к каноническому виду