Матрица
 Скачать 213.08 Kb. Скачать 213.08 Kb.
|
|
Матрица – прямоугольная таблица чисел, обозначающая коэффициенты при неизвестных в системе уравнений. Пример: 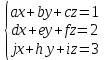 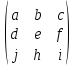 * * Диагональный вид матрицы – матрица, в которой все элементы кроме главной диагонали равны нулю. 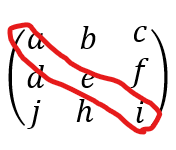 - Главная диагональ. - Главная диагональ.Пример: 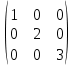 Другими словами: диагональный вид матрицы — это матрица (система уравнений), в которой в каждой строке (уравнении) находится лишь одна неизвестная переменная (с каким-то коэффициентом), и только в этой строке. Как привести матрицу к диагональному виду Представим систему уравнений: 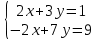 Как можно ее решить? Можно в одном уравнении выразить одну переменную через другую и подставить в другое уравнение, потом полученное значение одной переменной подставить в наше прошлое, где мы выражали первую переменную через вторую, и мы получим ответ. Но есть способ проще. В системе уравнений можно прибавлять/вычитать одно уравнение из другого, предварительно умножив на любое число. И чтобы было реально легко, мы делаем так, чтобы убралась одна из переменных. В нашем случае легче всего просто прибавить к первому уравнению второе, тогда иксы уничтожатся, останется только игрек, который легко посчитать: 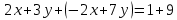 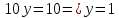 Ну а икс можно будет потом просто найти, подставив найденное значение игрека. НО, что мы сейчас делали? Давайте посмотрим, что происходило бы в матрице: 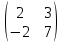 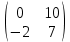 Мы сделали ноль вместо одного из элементов! Что мы для этого делали, если рассматривать чисто матрицу? Мы вычли одну строку чисел из другой, предварительно умножив на любое свое число (в нашем случае 1). А значит, что все остальные ячейки превращаются в ноль точно по такому же алгоритму. Я объяснил, как это работает в системе уравнений, я объяснил, что при этом происходит в матрице, теперь расскажу реальный нормальный алгоритм, чтобы не наобум действовать, а оптимально приходить к конечному варианту. 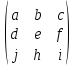 – Вот у нас есть матрица. Нам нужно сохранить какие-то числа на местах – Вот у нас есть матрица. Нам нужно сохранить какие-то числа на местах 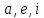 , остальные части матрицы (коэффициентами их называют) должны быть равны нулю. Будем работать по порядку. Сначала делаем все нули в первом столбце, не обращая внимания на то, что будет при этом твориться в остальных. Для этого нужно помножить , остальные части матрицы (коэффициентами их называют) должны быть равны нулю. Будем работать по порядку. Сначала делаем все нули в первом столбце, не обращая внимания на то, что будет при этом твориться в остальных. Для этого нужно помножить 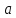 на такое число, чтобы получилось на такое число, чтобы получилось 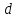 , и потом вычесть из второй строки первую, тогда коэффициент при , и потом вычесть из второй строки первую, тогда коэффициент при 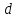 станет нулем, потом также и с третьей строкой. Если же множитель для станет нулем, потом также и с третьей строкой. Если же множитель для 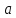 получается не целый, то можно для начала помножить вторую строку на что-то, чтобы это новое получается не целый, то можно для начала помножить вторую строку на что-то, чтобы это новое 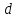 уже нацело делилось на уже нацело делилось на 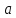 , тогда будет удобно и нормально. , тогда будет удобно и нормально. Помножая строку мы типа делаем вот так: 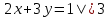 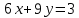 Ничего в принципе не изменилось, но зато теперь коэффициент при 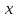 делится нацело на 3. делится нацело на 3. Когда мы проделали это с первым столбцом и у нас осталось там лишь одно число, то мы идем и то же самое делаем со вторым и третьим и так далее столбцом, НО, оставляем коэффициенты именно на главной диагонали, чтобы было удобно. Если всё будет легко, то можно и начинать пользоваться свойствами матриц / определителей, чтобы облегчить себе жизнь. Например – можно переставлять строки в матрице местами. Ведь нет разницы в том – какое уравнение ты запишешь первым в системе уравнений. Алгоритм приведения к диагональному виду, описанный мною выше, называется алгоритмом Гаусса-Жордана. И создан он, чтобы легко и быстро решать такие вот системы уравнений, где куча неизвестных, большие коэффициенты и т.п. Вот вообще хороший пример, иллюстрирующий всё, что я тут описал выше:  Хотя, может быть не совсем всё… ну ладно, думаю всё же стало понятнее. Взято отсюда: Нахождение решения СЛУ и обратной матрицы методом Гаусса-Жордана (mathprofi.ru) Всем пока |
