особые точки ду 2 го порядка. курсовая работа особые точки ду 2 го порядка. Задача нахождение решения уравнения, удовлетворяющего заданным начальным условиям, как и в случае уравнения первого порядка, называется

• Название: Задача нахождение решения уравнения, удовлетворяющего заданным начальным условиям, как и в случае уравнения первого порядка, называется
• Анкор: особые точки ду 2 го порядка
• Дата: 05.03.2023
• Размер: 157.68 Kb.
• Имя файла: курсовая работа особые точки ду 2 го порядка.docx
• Тип: Задача; #969894

Введение

Дифференциальное уравнение второго порядка связывает независимую переменную, искомую функцию и ее первую и вторую производные. В частных случаях в уравнении могут отсутствовать x, и . Однако уравнение второго порядка обязательно должно содержать вторую производную .

Дифференциальное уравнение второго порядка в общем случае имеет вид:



или, если это возможно, в виде, разрешенном относительно второй производной:

.

Как и в случае уравнения первого порядка, для такого уравнения справедлива теорема.

Теорема о существовании и единственности решения ДУ второго порядка. Пусть в уравнении функция и ее частные производные по у и по непрерывны в некоторой области G изменения переменных x, и . Тогда, какова бы ни была внутренняя точка (х₀; у₀; ) этой области, данное уравнение имеет единственное решение , удовлетворяющее начальным условия: у (х₀) = у₀ и .

Задача нахождение решения уравнения , удовлетворяющего заданным начальным условиям, как и в случае уравнения первого порядка, называется задачей Коши.

Общим решением дифференциального уравнения второго порядка называется функция , которая зависит от двух произвольных постоянных С₁ и С₂ и удовлетворяет условиям:

3) она является решением этого дифференциального уравнения при любых конкретных значениях постоянных С₁ и С₂;

4) каковы бы ни были начальные условия, существуют единственные значения постоянных С₁ = С₁₀ и С₂ = С₂₀ такие, что функция является решением уравнения и удовлетворяет этим начальным условиям.

Значения постоянных С₁₀ и С₂₀ можно найти из системы уравнений

.

Частным решением дифференциального уравнения второго порядка называется всякое решение уравнения , полученное из общего решения при конкретных значениях постоянных С₁ = С₁₀ и С₂ = С₂₀

Дифференциальные уравнения второго порядка, допускающие понижение порядка

Преобразование дифференциального уравнения второго порядка, в ходе которого с помощью замены переменной его сводят к уравнению первого порядка, называется понижением порядка.

Простейшими уравнениями, допускающими понижение порядка, являются следующие:

1) ;

2) ;

3) .

Рассмотрим последовательно, как осуществляется понижение порядка и как интегрируется каждое из указанных уравнений.

1. Уравнение .

Принцип решения этого типа уравнений мы рассмотрели в примере.

Введем новую функцию v (x), положив , тогда . Подставив полученные выражения в уравнение , получим:

или



.

Возвращаясь к замене, получим

или





или



2. Уравнение .

Это уравнение не содержит явно искомой функции у. Вводя, как и в предыдущем случае, новую функцию и замечая, что , получаем уравнение превого порядка относительно функции v (x):

.

Допустим, что найдено общее решение этого уравнения

v = φ (x, C₁).

Заменяя в этом решении функцию v на , получаем:

или .

Отсюда общее решение уравнения будет иметь вид:

.

3. Уравнение .

Для понижения порядка уравнения введем новую функцию v (y), зависящую от у, полагая .

Продифференцируем это равенство по х, помня, что у является функцией от переменной х, т.е. v (y) – сложная функция:

.

Т.к. , то .

Подставляя выражения и в исходное уравнение, получим уравнение первого порядка относительно функции v (y):

.

Пусть функция является общим решением этого уравнения. Вспоминая, что ,получаем уравнение с разделяющимися переменными:

или .

Интегрируя его, находим общий интеграл первоначального уравнения:



.

Дифференциальные уравнения

Дифференциальное уравнение второго порядка называется линейным однородным дифференциальным уравнением (ЛОДУ) с постоянными коэффициентами, если оно имеет вид:

,

где p и q – некоторые действительные числа.

Для нахождения общего решения ЛОДУ достаточно найти два его различных частных решения и . Тогда общее решение ЛОДУ будет иметь вид

,

где С₁ и С₂ – произвольные независимые постоянные.

Леонард Эйлер предложил искать частные решения ЛОДУ в виде

,

где k – некоторое число.

Дифференцируя эту функцию два раза и подставляя выражения для у, у' и у" в уравнение , получим:

,







Полученное уравнение называется характеристическим уравнением ЛОДУ. Для его составления достаточно в исходном уравнении заменить у", у' и у соответственно на k², k и 1:

Решив характеристическое уравнение, т.е. найдя корни k₁ и k₂,мы найдем и частные решения исходного ЛОДУ.

Характеристическое уравнение есть квадратное уравнение, его корни находятся через дискриминант

.

При этом возможны следующие три случая^[2].

Случай 1. Дискриминант больше нуля, следовательно, корни k₁ и k₂ действительные и различные:

k₁ ¹ k₂

В этом случае общее решение ЛОДУ имеет вид:

,

где С₁ и С₂ – произвольные независимые постоянные.

Случай 2. Дискриминант равен нулю, следовательно, корни k₁ и k₂ действительные и равные:

k₁ = k₂ = k

В этом случае общее решение ЛОДУ имеет вид

,

где С₁ и С₂ – произвольные независимые постоянные.

Случай 3. Дискриминант меньше нуля. В этом случае уравнение не имеет действительных корней:

, корней нет.

В этом случае общее решение ЛОДУ имеет вид

,

где С₁ и С₂ – произвольные независимые постоянные,

, .

Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами сводится к нахождению корней характеристического уравнения и использованию формул общего решения уравнения (не прибегая к вычислению интегралов).

Алгоритм нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами:

1. Привести уравнение к виду , где p и q – некоторые действительные числа.

2. Составить характеристическое уравнение .

3. Найти дискриминант характеристического уравнения.

4. Используя формулы (см. Таблицу 1), в зависимости от знака дискриминанта записать общее решение.
Таким образом, нам надо найти общее решение ЛОДУ, что сделать не трудно, и отыскать какое-нибудь частное решение исходного ЛНДУ. Вид этого частного решения устанавливается по виду правой части исходного ЛНДУ, т.е. по виду функции r (x).

Рассмотрим некоторые возможные случаи.

1. Функция r (x) – многочлен степени т:



Тогда частное решение следует искать в виде

,

где k – число корней характеристического уравнения, равных нулю, т.е.

k = 0, если q ¹ 0

k = 1, если q = 0, p ¹ 0

k = 2, если q = 0, p = 0.

2. Функция r(x) – произведение числа на показательную функцию:



В этом случае частное решение следует искать в виде

,

где n – число корней характеристического уравнения, равных а, т.е.

п = 0, если k₁ ¹ а, k₂ ¹ а,

п = 1, если k₁ = а, k₂ ¹ а или k₁ ¹ а, k₂ = а

п = 2, если k₁ = k₂ = а

3. Функция r (x) – сумма тригонометрических функций вида:



где А, В, b – некоторые действительные числа, причем b ¹ 0.

Тогда частное решение следует искать в виде

,

где s = 1, если p = 0, q > 0,

s = 0, во всех других случаях.

Подводя итог, составим алгоритм нахождения общего решения ЛНДУ второго порядка с постоянными коэффициентами со специальной правой частью:

1. Привести уравнение к виду , где p и q – некоторые действительные числа, r (x) – некоторая функция.

2. Составить соответствующее однородное уравнение: .

3. Найти – общее решение этого однородного уравнения, используя Таблицу 1.

4. Используя Таблицу 2, определить общий вид частного решения ЛНДУ.

5. Найти числа С_i и записать – частное решение исходного неоднородного уравнения.

6. Записать искомое общее решение ЛНДУ по формуле:



Приложение 1

Вывод формул общего решения

ЛОДУ второго порядка с постоянными коэффициентами

Случай 1. Дискриминант больше нуля, следовательно, корни k₁ и k₂ действительные и различные:

k₁ ¹ k₂

В этом случае частными решениями ЛОДУ являются функции и . Следовательно, общее решение ЛОДУ имеет вид:

,

где С₁ и С₂ – произвольные независимые постоянные.

Случай 2. Дискриминант равен нулю, следовательно, корни k₁ и k₂ действительные и равные:

k₁ = k₂ = k

В этом случае имеем лишь одно частное решение , а для нахождения общего решения ЛОДУ нам необходимо два различных частных решения. Как найти второе?

Покажем, что наряду с частным решением ЛОДУ будет и .

Действительно, подставим функцию в исходное уравнение , найдя предварительно ее производные. Имеем:



ß



.

Но k – это корень характеристического уравнения, следовательно, ; кроме того, по теореме Виета или , т.е. . Тогда

.

Это значит, что функция является решением ЛОДУ.

Таким образом, у нас есть два различных частных решения ЛОДУ: и , следовательно, общее решение ЛОДУ имеет вид

,

где С₁ и С₂ – произвольные независимые постоянные.

Случай 3. Дискриминант меньше нуля. В этом случае уравнение не имеет действительных корней, корни квадратного уравнения в этом случае – комплексные числа.

Комплексные числа – особое числовое множество, в котором можно извлекать квадратный корень из отрицательных чисел.

В этом множестве есть элемент i, который называется мнимая единица и обладает свойством: , откуда .

При таких условиях можно извлекать корень из любого отрицательного числа: .

Любое комплексное число можно представить в виде

,

где a и b – действительные числа. При этом a называется действительной частью комплексного числа, bi называется мнимой частью комплексного числа.

Нетрудно доказать, что привычное нам множество действительных чисел R является подмножеством множества комплексных чисел С: R Ì С.

Но вернемся к нашему ЛОДУ, для которого характеристическое уравнение имеет отрицательный дискриминант: .

Найдем корни характеристического уравнения :



Таким образом, характеристическое уравнение имеет два различных комплексных корня и ,

где , .

Следовательно, частными решениями исходного ЛОДУ будут функции и .

К сожалению, эти частные решения содержат мнимую единицу, что не очень хорошо, т.к. мы должны найти решение ЛОДУ на множестве действительных чисел. Попробуем преобразовать наши частные решения так, чтобы они не содержали мнимую единицу.

Воспользуемся формулами Эйлера:

, .

Тогда

,

.

Теперь мы можем найти два действительных частных решения:

и .

В итоге общее решение ЛОДУ имеет вид

,

гдеС₁иС₂–произвольные независимые постоянные,

,

Особые точки Дифференцальных уравнений 2-го порядка

Если в окрестности точки (x₀, y₀) плоскости для уравнения выполняются условия существования и единственности решения задачи Коши (непрерывность f(x, y) и ), то через эту точку проходит единственная интегральная кривая. Если эти условия нарушаются, точку (x₀, y₀) называют особой точкой дифференциального уравнения. Через особую точку может не проходить ни одной интегральной кривой (т.е. задача , y(x₀) = y₀ не имеет решения); может проходить одна интегральная кривая; может проходить несколько интегральных кривых. Особые точки могут образовать кривую, которая сама является интегральной кривой уравнения. Решение уравнения, в каждой точке которого нарушается его единственность, называют особым решением.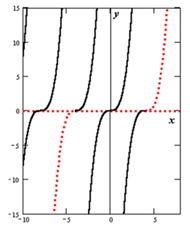



Для примера рассмотрим уравнение . Здесь - непрерывна в любой точке (x, y), но - не имеет конечного предела при , т.е. в любой точке (x, y) при y = 0 нарушается условие существования непрерывной производной . Следовательно, любая точка (x, 0) является особой точкой уравнения. Прямая y = 0, очевидно, интегральная кривая уравнения (функция y = 0 удовлетворяет уравнению). Найдём общее решение этого уравнения:



Несколько таких функций приведено на рисунке справа вверху вместе с решением y = 0. В любой точке (x, 0) нарушается единственность решения, таким образом, решение y = 0 - особое. На самом деле через любую точку (x, 0)проходит бесконечное количество интегральных кривых, так как любая кривая, составленная из частей особого и неособых решений (одна такая кривая выделена красным пунктиром), также является интегральной кривой.

Решение примеров

ЗАКЛЮЧЕНИЕ

Особая точка дифференциального  уравнения - точка, в которой одновременно обращаются в нуль и числитель  и знаменатель правой части дифференциального уравнения

где Р и Q - непрерывно дифференцируемые функции.

Предполагая, что особая точка расположенна в начале координат и используя Тейлора формулу, можно представить уравнение выше в виде:

  где P(x, у) и Q(x, у)- бесконечно малые по отношению к .Характер поведения интегральных кривых около особой точки зависит от корней l1 и l2 характеристического уравнения.

В окрестности особой точки  система может обладать очень  сложной динамикой. В зависимости  от собственных значений матрицы, различают  четыре типа невырожденных особых точек  линейных систем: узел, седло, фокус, центр. Кроме основных типов появляются так называемые сложные: седло-узел, центро-фокус и т.д. Они образуются как результат слияния точек покоя основных типов.

Мы имеем классы устойчивых и неустойчивых точек. Ясно, что наличие  исключительных направлений, заключается  в одну из областей 1 или 2, исключает  возможность устойчивой особой точки. Но вообще наличие исключительного направления не препятствует устойчивости точки, даже наличию центра. Отсутствие исключительных направлений приводит, вообще говоря, к двум возможным случаям: или особая точка есть фокус, либо устойчивая особая точка. Если же исключительные направления имеются в конечном числе, тогда легко видеть, когда могут возникать в окрестности начала координат эллиптические, гиперболические и параболические области.

Гиперболическая – в том  случае, если, рассматривая два средних  исключительных направления, мы убеждаемся, что оба они могут быть заключены  в область .

Эллиптические получаются в  том случае, если два соседних исключительных направления могут быть заключены  в область типа 1(рис. д).

Наконец, если правая часть  характеристического уравнения  тождественно обращается в 0, то только по конечному числу направлений  в особую точку могут входить  интегральные кривые.