Лабораторная работа 4 Ексель. Лаб Раб 4 Реш Уравн EXEL. В общем виде любое уравнение одной переменной принято записывать так, при этом корнем
 Скачать 0.51 Mb.
|
|
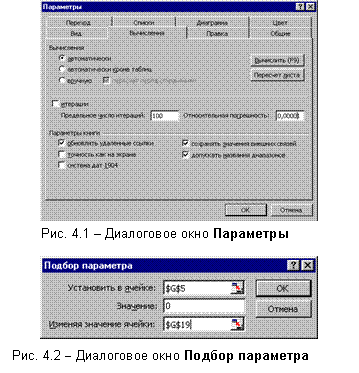
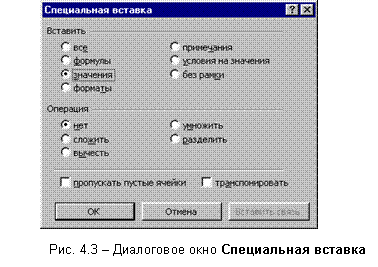
Лабораторная работа 4. Численное решение Уравнений и систем уравнений Область локализации корней В общем виде любое уравнение одной переменной принято записывать так  , при этом корнем (решением) называется такое значение x*, что  оказывается верным тождеством. Уравнение может иметь один, несколько (включая бесконечное число) или ни одного корня. Как легко видеть, для действительных корней задача отыскания решения уравнения легко интерпретируется графически: корень есть такое значение независимой переменной, при котором происходит пересечение графика функции, стоящей в левой части уравнения f(x), с осью абсцисс.Например, для уравнения 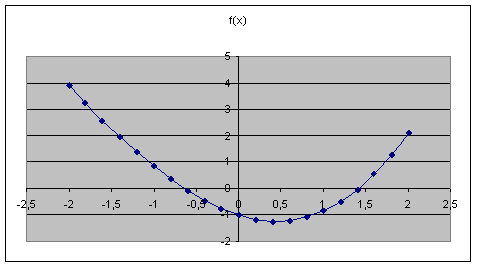 выполним преобразование и приведем его к виду f(x)=0 т.е.  . График этой функции представлен на рисунке 1. Очевидно, что данное уравнение имеет два действительных корня – один на отрезке [-1, 0] , а второй – [1, 2]. Рисунок 1. График функции  Таким образом, можно приблизительно определять область локализации корней уравнения. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён. Критериисходимостиприрешенииуравнений Абсолютная погрешность - абсолютное изменение приближения на соседних шагах итерации  Относительная погрешность - относительное изменение приближения на соседних шагах итерации  Близость к нулю вычисленного значения левой части уравнения (иногда это значение называют невязкойуравнения,так как для корня невязка равна нулю)  Часть 1. Решение уравнений Задание 1. Нахождение корней полиномов при помощи табулирования и сервисной функцииПодбор параметра. Известно, что если функция, определенная в интервале [a,b], имеет значения F(а) и F(b) с разными знаками, то в интервале [a,b] есть, по крайней мере, один корень. Построить алгоритм нахождения корней уравнений с заданной точностью EPS следующим образом. 1. Определить (локализовать) начальный интервал [A,B], где находятся корни можно графически или следующим приемом. Дляполиномов  модули всех корней xk , k= 1…n расположены в круговом кольце  , (4.1)г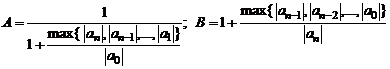де  .Таким образом, положительные корни лежат в интервале [A, B], а отрицательные корни в интервале [B,A]. 2. Табулируя полином в найденных начальных интервалах (например, с шагом (ВА)/10), составить таблицу {x, P(x)}. 3. Определить две соседние ячейки х, где функция меняет свой знак. Одно из значений (для которого значение функции ближе к нулю) принять за начальное приближение к корню полинома. 4. Уточнение корня производится методом последовательных приближений с помощью сервисной команды Подбор параметра(меню Сервис). Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры (СервисПараметрыВычисления) (рис. 4.1). 5. Открыть диалоговое окно Подбор параметра (рис. 4.2). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома. В поле Значение ввести 0 (т.е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, отведенной для переменной х, где должно находиться начальное приближение к корню полинома.
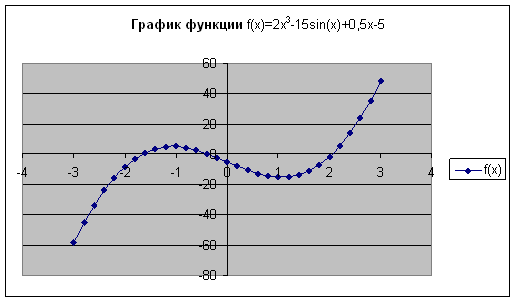
Примечание. В этой ячейке должно содержаться числовое значение, а не формула, его вычисляющая. Для того, чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 4.3). В появившемся диалоговом окне отметить Значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра. 6. После подбора параметра (ОК) х получит значение корня. Процесс повторяется для всех найденных начальных приближений в диапазоне, определяемом формулой (4.1).
Данные для решения взять из таблицы 4.1. Корни найти с точностью EPS=0,00001. Таблица 4.1 Полиномы
Пример решения уравнения, используя “Подбор параметра” Например, найдем все корни уравнения 2x3-15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3; 3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня.
Рисунок 4. Поиск приближенных значений корней уравнения Выполните команду меню Сервис/Параметры,во вкладкеВычисления установите относительную погрешность вычислений E=0,00001, а число итераций N=1000, установите флажок Итерации. Выполните команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 9) заполните следующие поля: Установить в ячейке: в поле указывается адрес ячейки, в которой записана формула правой части функции; Значение: в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0); Изменяя значение: в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула. 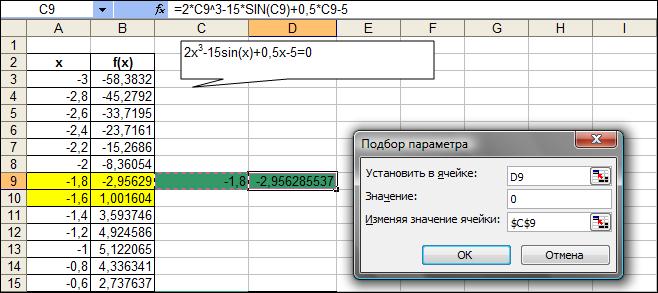 Рисунок 5. Диалоговое окноПодбор параметрадля поиска первого корня После щелчка на ОК получим значение первого корня -1,65793685. Выполняя последовательно операции аналогичные предыдущим, вычислим значения остальных корней: -0,35913476 и 2,05170101. Задание 2.Нахождение корней нелинейных уравнений с помощью метода итераций. Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций уравнение представляют в виде x=F(x) и записывают итерационную схему  , (4.2)с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, которое выбирается самостоятельно. Достаточное условие сходимости процесса: в окрестности корня | F /(x)| <1. Порядок действий в Excel может быть следующий. 1. Представить данное уравнение в виде x=F(x). 2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность. 3. В первую ячейку первой строки таблицы занести значение 0, во вторую – начальное приближение. 4. В следующие строки занести, соответственно, номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5). 5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения EPS. Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений – метод Ньютона. Его итерационная схема имеет вид  . (4.3)Сравнивая (4.2) и (4.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (4.3). В большинстве случаев метод Ньютона сходится быстрее. Данные для решения взять из таблицы 4.2. Точность решения EPS=0,0001. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат – очередное приближение к корню. Задание 3. Нахождение корней нелинейных уравнений методом бисекции. Если метод итераций сходится не всегда, то метод бисекции (или метод деления отрезка пополам, или метод дихотомии) – безусловно сходящийся метод нахождения корней нелинейного уравнения F(x)=0, лишь бы был известен отрезок, на котором расположен корень уравнения. Пусть непрерывная функция F(x) меняет знак на концах отрезка [a,b], т.е. F(a)*F(b) < 0. Назовем такой отрезок отрезком локализации корня: на нем есть, по крайней мере, один корень. Найдем координату середины этого отрезка c=(a+b)/2 и рассмотрим два получившихся отрезка [a,c] и [c,b]. Если F(a)*F(с) < 0, то корень находится на отрезке [a,c], в противном случае – на отрезке [с,b]. Процесс деления все новых и новых отрезков локализации корня продолжаем до тех пор, пока длина отрезка не станет меньше заданной величины точности решения EPS. Таблица 4.2 – Нелинейныеуравнения
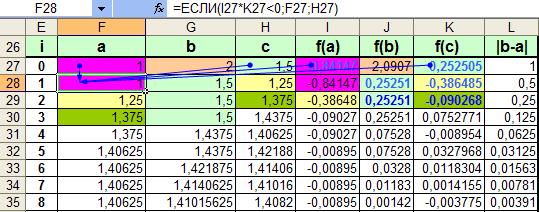
При использовании Excel достаточно внести в некоторые ячейки, лежащие в одной строке, формулы, осуществляющие: вычисление значений левой и правой границы отрезков локализации; нахождение середины отрезка; вычисление произведения значений функций в левой и правой границах отрезка (для контроля правильности алгоритма); проверку на точность решения (аналогично предыдущему заданию). Затем формулы копируются вниз по столбцам до тех пор, пока не будет найден корень с заданной степенью точности EPS=0,0001. Данные для решения взять из таблицы 4.2, то есть решить одно и то же уравнение двумя способами. Пример решения уравненияметодом бисекции (дихотомии) Найти решение заданного уравнения методом дихотомии с точностью до 10-5. Создать расчетную схему на основе метода дихотомии для уравнения: на отрезке [1, 2]Данный метод заключается в проверке на каждой итерации условия: если f(a)f(с)<0  и выбор соответствующего отрезка для следующей итерации.
|
