Лабораторная работа 4 Ексель. Лаб Раб 4 Реш Уравн EXEL. В общем виде любое уравнение одной переменной принято записывать так, при этом корнем
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Часть 2 Матричные (групповые)операции Табличные формулыили формулы массива– очень мощное вычислительное средство Excel, позволяющее работать с блоками рабочего листа как с отдельными ячейками. Табличные формулы в качестве результата возвращают массив значений. Поэтому перед вводом такой формулы необходимо: выделить диапазон ячеек, куда будут помещены результаты; набрать формулу; по окончании ввода нажать комбинацию клавиш Ctrl+Shift+Enter!!! Формула вводится во все ячейки выделенного интервала. При активизации любой ячейки из интервала, содержащего формулу массива, в строке формул отображается введенная формула, заключенная в фигурные скобки. Именно фигурные скобки являются признаком табличной формулы. Для выделения всего блока, содержащего табличную формулу, необходимо выделить одну из его ячеек, после чего нажать комбинацию клавиш Ctrl+/. Невозможно редактировать содержимое только одной ячейки из интервала с табличной формулой. Изменить можно только весь блок целиком, для чего он и должен быть предварительно выделен. Операции с матрицами К простейшим операциям с матрицами принято относить следующие: сложение и вычитание матриц, умножение и деление матрицы на число, перемножение матриц, транспонирование, вычисление обратной матрицы. Умножение (деление) матрицы на число, сложение (вычитание) матриц в Excel реализуются достаточно просто: с помощью обычных формул (поэлементное сложение или вычитание, умножение или деление на число), либо с использованием табличных формул, как это описано ниже. Сложение матриц Например, пусть необходимо сложить две матрицы размера 33. Элементы первой матрицы (9 элементов) разместим в интервале A1:C3, второй – в диапазоне E1:G3. Под результат выделим интервал A5:C7. После чего, не снимая выделения, введем формулу =A1:C3+E1:G3, нажав комбинацию клавиш Ctrl+Shift+Enter. В ячейках интервала A5:C7 отобразится результат – сумма соответствующих элементов матриц, а в строке формул мы увидим {=A1:C3+E1:G3}. Умножение матрицы на число Пусть вместо сложения нам надо умножить первую матрицу на число 2. Для этого перемещаемся внутрь интервала A5:C7, выделяем его, нажав комбинацию Ctrl+/,вносим в формулу исправления =A1:C3*2 и нажимаем Ctrl+Shift+Enter. В интервале A5:C7 увидим результат умножения, а в строке формул – табличную формулу {=A1:C3*2}. Для остальных матричных операций в Excel предусмотрены функции:
Первая из этих функций в качестве результата возвращает число (определитель матрицы), поэтому вводится как обычная формула (Enter). Последние три возвращают блок ячеек, поэтому должны вводиться как табличные формулы (Ctrl+Shift+Enter). Задание 4. Решение систем линейных алгебраических уравнений. Для работы с матрицами используем (Вставка функцииМатематические): МОБР вычисление обратной матрицы А-1; МОПРЕД вычисление определителя матрицы D; МУМНОЖ нахождение произведения двух матриц. С их помощью можно решать системы линейных алгебраических уравнений вида 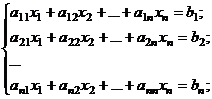 (4.4) (4.4)или в матричном виде А*Х=В, где А= {aij}– матрица коэффициентов при неизвестных; В = {bij} – вектор-столбец правых частей уравнений; Х = {xij} – вектор-столбец неизвестных. Способ 1 (метод обратной матрицы).Решение имеет вид Х = А–1*В, где А–1 – матрица, обратная по отношению к матрице А. С помощью функции МОБР находится обратная матрица, а затем с помощью функции МУМНОЖ она перемножается с вектором-столбцом правых частей уравнений. Напоминание. При работе с матрицами перед вводом формулы необходимо выделить область на рабочем листе, куда будет выведен результат вычисления, а после задания исходных данных в поле функции выйти не как обычно, нажатием клавиши Enter или кнопки ОК, а нажатием клавиш Ctrl + Shift + Enter. 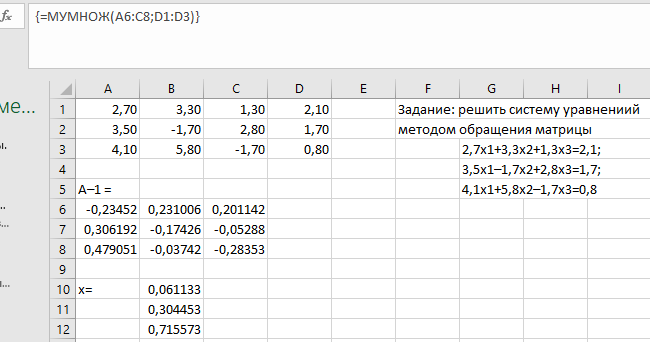 Способ 2 (правило Крамера).Если определитель , составленный из коэффициентов при неизвестных, отличен от нуля, то решение имеет вид x j = j/ , j=1...n. (4.5) Здесь j – дополнительный определитель, полученный из главного определителя системы путем замены его j-го столбца вектором-столбцом В. С помощью функции МОПРЕД находятся главный и дополнительные определители, и по формулам (4.5) вычисляются корни СЛАУ. 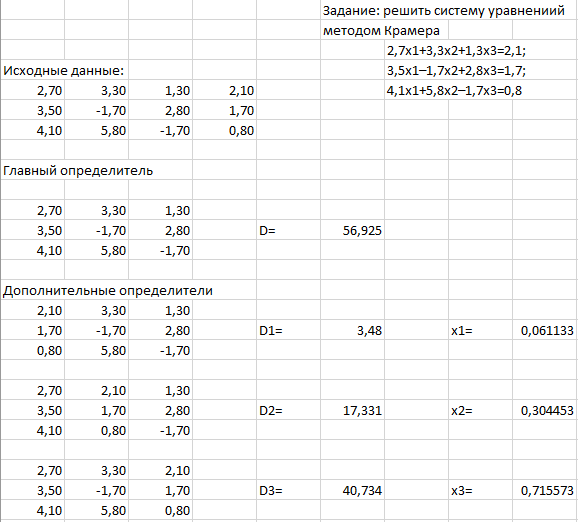 Способ 3 (метод исключений Гаусса).Этот метод основан на приведении матрицы системы к треугольному виду, что достигается последовательным исключением неизвестных из уравнений системы. Предположим, что в (4.4) a11 0. Разделим первое уравнение системы на a11 (этот коэффициент называется ведущим или главным элементом), получим 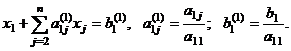 Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент ai1 (i=2,3,, n). Эти n–1 уравненийпринимаютвид 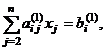 где Далее аналогичную процедуру выполняют с этой системой, оставляя в покое первое уравнение. Только теперь делят на другой ведущий элемент a22(1) 0. В результате исключения неизвестных приходим к СЛАУ с верхней треугольной матрицей с единицами на главной диагонали: 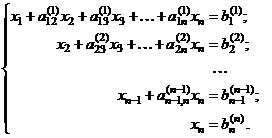 (4.6) (4.6)Индексы над коэффициентами означают, сколько раз данное уравнение преобразовывалось. Прямой ход метода Гаусса завершен. Обратный ход метода Гаусса заключается в нахождении неизвестных xn, xn-1, ... ,x1 , причем в указанном порядке. В этом списке xn уже определено из последнего уравнения системы (4.6), а общая формула обратного хода имеет вид: 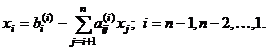 Проиллюстрируем этот алгоритм на примере решения системы из трех уравнений. 1. Располагаем на листе Excel матрицу коэффициентов и столбец правых частей (т.н. расширенная матрица 34), например, в ячейках А4:D6 (рис. 4.4). 2. Выделяем диапазон ячеек А8:D8 и вводим формулу: {=A4:D4/A4}. Фигурные скобки появляются автоматически при вводе формулы комбинацией клавиш Shift+Ctrl+Enter, как признак того, что идет работа не с отдельными ячейками, а с массивами. 3. Выделяем диапазон ячеек А9:D9, вводим формулу {=A5:D5-$A$8:$D$8*B5} и копируем эту формулу в диапазон ячеек А10:D10. В ячейках А9 и А10 появились нули. 4. В ячейки А12:D12 копируем значения первой строки расширенной матрицы А8:D8, в ячейки А13:D13 – формулу {=A9:D9/B9}. При этом второй элемент главной диагонали матрицы коэффициентов становится равным единице.
В ячейки А14:D14 вводим формулу {=A10:D10–$A$13:$D$13*B10}. 5) В ячейки А16:D17 копируем значения первых двух строк расширенной матрицы (А12:D13), а в ячейки А18:D18 – формулу {=A14:D14/C14}. Прямой ход метода Гаусса завершен: получилась верхняя треугольная матрица с диагональными элементами, равными 1. Решить тремя способами систему линейных алгебраических уравнений, взяв данные для решения из таблицы 4.3. Проверить найденное решение умножением матрицы коэффициентов на вектор-столбец решения. Таблица 4.3 – Системылинейныхалгебраическихуравнений
Продолжениетаблицы 4.3
Продолжениетаблицы 4.3
|