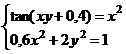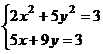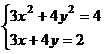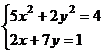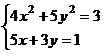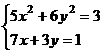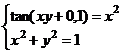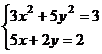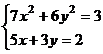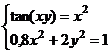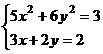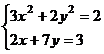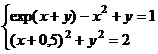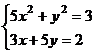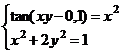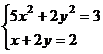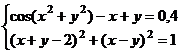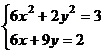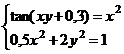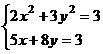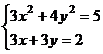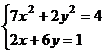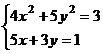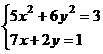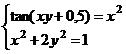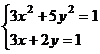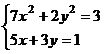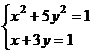Лабораторная работа 4 Ексель. Лаб Раб 4 Реш Уравн EXEL. В общем виде любое уравнение одной переменной принято записывать так, при этом корнем
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
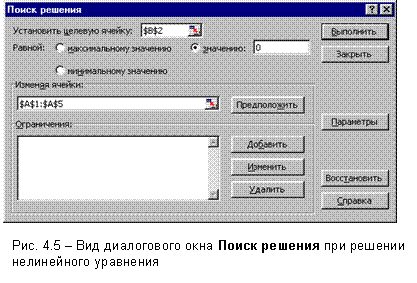
Задание 5. Решение систем нелинейных уравнений. С помощью сервисной программы Поиск решения (Сервис|Поискрешения) в Excel можно решать системы нелинейных уравнений. В общем случае система нелинейных уравнений имеет вид: 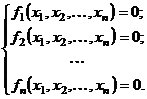 (4.7) (4.7)Составим новую функциюF(x1, х2, ..., хn),представляющую собой сумму квадратов правых частей уравнений: Очевидно, переменные x1, х2, ..., хn , являющиеся решением системы (4.7), с необходимостью и достаточностью являются также решением уравнения Путь решения следующий. На листе Excel отводим ячейки для неизвестных данной системы уравнений, например с А1 по А5 (если пять переменных), и вводим туда начальные приближения. В ячейку В2 вводим формулу, вычисляющую функцию (4.8). Открываем диалоговое окно Поиск решения (рис. 4.5). В поле Установить целевую ячейку вводим В2, в группе Равной устанавливаем переключатель в положение Значению и в поле ввода задаем 0. В поле Изменяя ячейки вводимдиапазонячеек А1:А5.
После нажатия на кнопку Выполнить будет найдено решение, которое поместится в ячейки А1:А5. В ячейке В2 будет вычислено значение левой части уравнения (4.9) с относительной погрешностью, задаваемой в диалоговом окне Параметры поиска решения . Примечание 1.При неудачном выборе вектора начального приближения решение может быть не найдено. Поэтому необходим предварительный анализ системы уравнений с целью определения лучшего (более близкого к корню) начального приближения. Например, для системы из двух уравнений можно затабулировать функцию (4.8) и в качестве начальных выбрать приближения, наиболее близкие к нулю. Примечание 2. Система уравнений может иметь несколько корней, поэтому необходим ее анализ и с этой стороны. Задавая разные начальные приближения, можно получить разные решения системы. Примечание 3. Более подробно о возможностях программы Поиск решения изложено в лабораторной работе 12. tan(ху+0,4)-x2 +0,6 x2 + 2 y2-1 Решить систему нелинейных уравнений, взяв данные из таблицы 4.4. Проверитьнайденноерешение. Таблица 4.4 – Системынелинейныхуравнений
Продолжениетаблицы 4.4
Построить поверхность, описываемую функциейF(x, y) в окрестности одного из корней, пользуясь описанием, приведенным в лабораторной работе 2. Пример1 решения уравнения, используя надстройку “Поиск решения” Например, найдем все корни уравнения 2x3-15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3;3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня. На рисунке 12 представлен пример заполнения окна Поиск решения для нахождения первого корня на отрезке [-2; -1]. 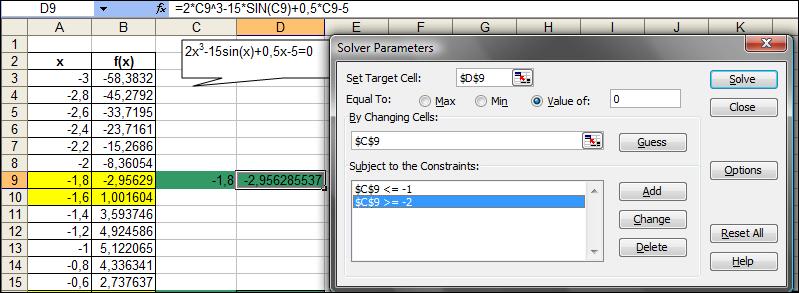 Рисунок 8. Пример решения уравнения при помощи надстройкиПоиск решения 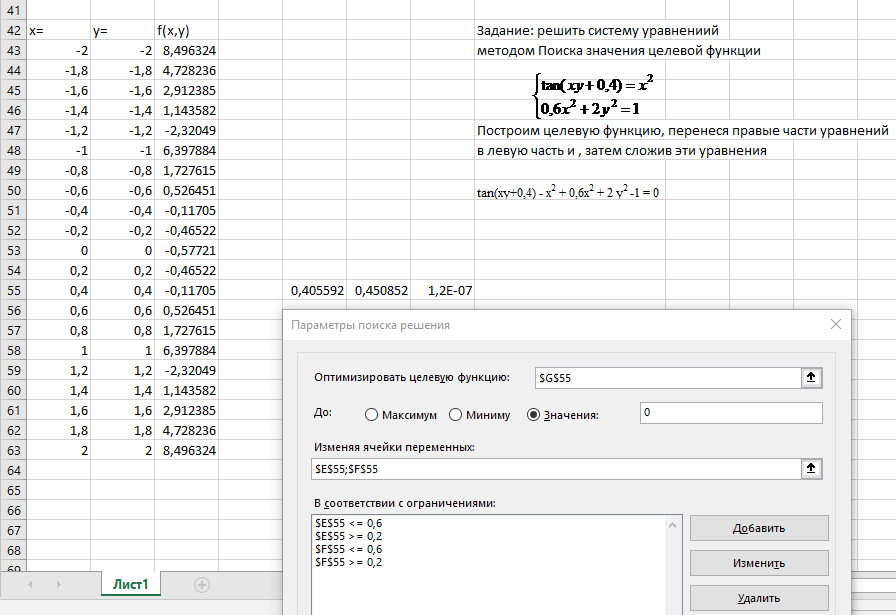 Рисунок 9. Пример2 решения уравнения при помощи надстройкиПоиск решения |