решение уравнений маткад. Нелин_уравнения. Практическая работа 5 Численное решение нелинейных уравнений в Mathcad (метод простых итераций)
 Скачать 318.5 Kb. Скачать 318.5 Kb.
|
Практическая работа №5Численное решение нелинейных уравнений в Mathcad (метод простых итераций) Цель работы:научиться решать нелинейное уравнение в Mathcad, используя вычислительный алгоритм метода простых итераций; Задание №1. Решить нелинейное уравнение методом итераций. Метод простых итераций является одним из наиболее важных способов численного решения уравнений. Этот метод состоит в следующем. Пусть дано уравнение f(x)=0, (1) где f(x) непрерывная функция, требуется определить вещественные корни этого уравнения. Запишем уравнение (1) равносильным уравнением x= Выберем каким-либо способом, например графически, приближенное значение корня x0 и подставим его в правую часть уравнения (2). Получим некоторое число x1= Подставим теперь в правую часть уравнения (3) вместо x0 число x1. Получим новое число x2= Рассмотрим реализацию алгоритма метода простых итераций в Mathcad на следующем примере. Найти действительные корни уравненияx-sin(x)=0.25 с точностью до трех значащих цифр. Установим формат чисел так, чтобы результаты вычислений отображались с нужным количеством знаков после десятичной точки (запятой). Для получения приближенного значения корня данного уравнения запишем его следующим образом: f(x):sin(x)+0.25 g(x):x Заметим, что функция f(x) является итерирующей функцией метода простых итераций. Построим графики функций f(x) и g(x), точка пересечения которых и даст приближенное значение корня исходного уравнений. Этим значением будет x0=1.2. Определим начальное значение для вычислений следующим образом: x0:1.2. Определим функцию первой производной итерирующей функции f(x) для проверки условия сходимости, вызвав, оператор дифференцирования из палитры вычислений (Calculus Palette): d(x): Вычислим значение функции d(x) в точке x0=1.2. Так как d(1.2)=0.3624<1, можно продолжать вычисления. Определим дискретный аргумент i:=0..9, задающий количество вычисляемых значений xi. Определим функцию вычисления приближений методом последовательных приближений в векторной форме: xi+1:f(xi) Для получения вектора результатов в свободном месте рабочего пространства Mathcad напишите: x=. Обратим внимание на то, что начиная с четвертого значения элементы вектора результатов остаются неизменными до трех знаков после десятичной точки (запятой). Это говорит о том, что сходимость результата с точностью до трех знаков достигнута на пятой итерации. Введите условие оценки погрешности вычислений Результат на экране:  Система уравнений для поиска приближенного решения графическим способом.  Графики функций f(x) и g(x). Точка пересечения этих графиков дает при-ближенное решение уравнения Начальное значение для вычисления приближений. П  Д Функция вычисления приближений. Вектор результатов Оценка погрешности вычислений  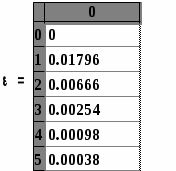 Так как по условию погрешность вычислений не должна различаться в трех значащих цифрах после десятичной точки (ε4 и ε5 не различаются в трех цифрах после десятичной точки), в качестве корня уравнения выбираем x4 К Задачи для самостоятельного решения. Методом простых итераций с точностью до трех значащих цифр решить следующие уравнения. x3-x-1=0 x5-x-0.2=0 Практическая работа №6Численное решение нелинейных уравнений в Mathcad (метод бисекции) Цель работы:научиться решать нелинейное уравнение в Mathcad, используя вычислительный алгоритм метода бисекции (половинного деления). Задание №1. Решить нелинейное уравнение методом бисекции. Метод бисекции (половинного деления) состоит в следующем. Пусть дано уравнение f(x)=0, (1) где f(x) непрерывная функция на [a, b] и f(a)f(b)<0. Требуется определить вещественные корни этого уравнения. Для нахождения корня уравнения на отрезке [a, b] нужно разделить этот отрезок пополам. Если Рассмотрим реализацию алгоритма метода половинного деления в Mathcad на следующем примере. Найти действительный корень уравненияx4+2x3-x-1=0. Деление продолжать до получения отрезка длиной ε ≤ 10-3. Определите левую часть нелинейного уравнения как функцию f(x). Построим график функции f(x), точка пересечения которого с осью и даст приближенное значение корня исходного уравнения. Определим по графику значения концов отрезка, содержащего корень уравнения: a=0, b=1. Задайте значения концов отрезка [a, b] в векторной форме. Для этого, используя палитру векторов и матриц, получите, оператор вектора на два элемента и заполните его идентификаторами концов отрезка a0 и b0. При помощи клавиши пробела выведите курсор за знак оператора, нажмите клавишу :, введите еще один оператор вектора на два элемента и заполните его значениями концов отрезка: 0 и 1. Задайте дискретную переменную i (от 0 до 10), определяющую количество этапов деления отрезка [a, b], за которое мы рассчитываем получить решение уравнения. Определите формулы вычисления концов отрезка на каждом этапе деления его пополам. На отрезке [ai, bi] серединой будет точка Если Подобная операция необходима для другого конца отрезка [ai, bi], для bi. Если  , то конец нового отрезка для вычислений bi+1 совпадет с точкой половинного деления отрезка, т.е. , то конец нового отрезка для вычислений bi+1 совпадет с точкой половинного деления отрезка, т.е. 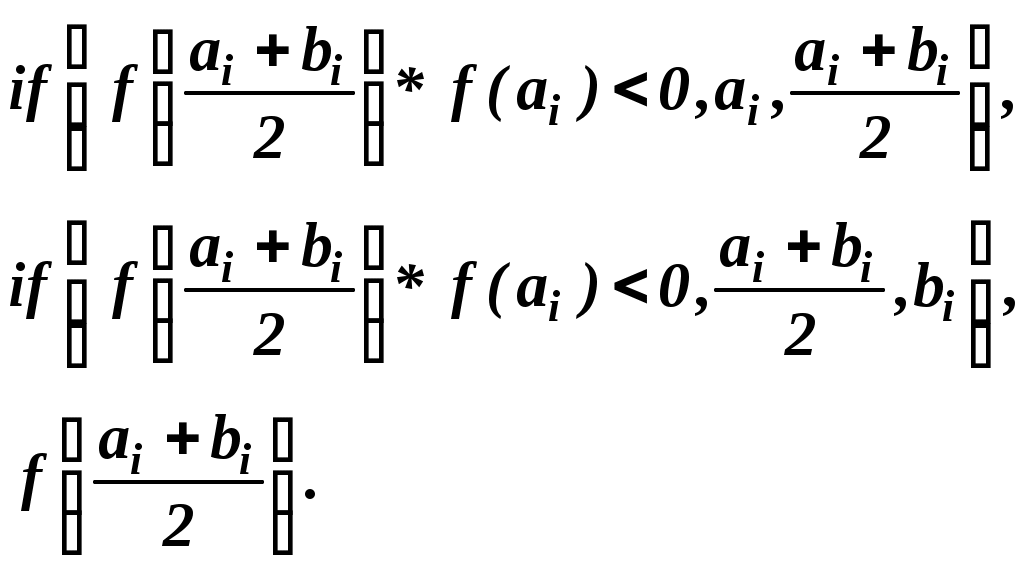 Условный оператор if работает следующим образом. Если логическое выражение, записанное в скобках, истинно, то переменная слева от знака := принимает значение выражения или величины, стоящей первой после логического выражения, в противном случае переменной присваивается значение выражения, или величины, стоящей на втором месте после логического выражения. Чтобы увидеть результат вычислений, введите последовательно a=, b=, g=. Вектор a покажет начала всех разделенных отрезков, b концы этих отрезков. Вектор g содержит значения функции f(x) в серединах всех отрезков [a, b]. Среди значений вектора a или вектора b будет корень исходного уравнения. Определим корень уравнения следующим образом. Вычислим длину отрезка [ai, bi] i=0,…,10, определив ее как Результат на экране: Л Локализация корня уравнения. 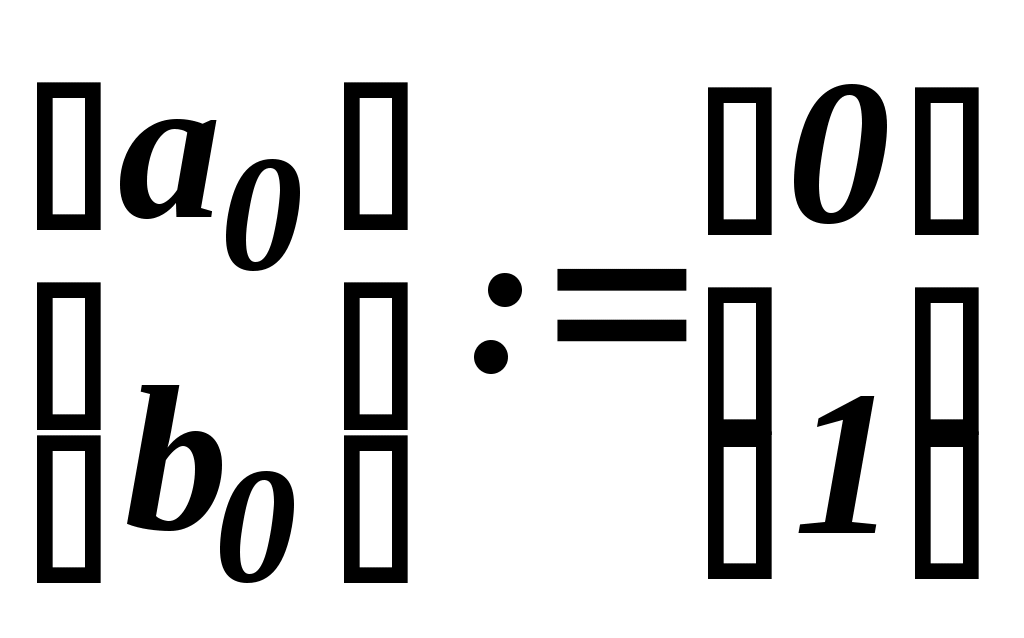 Значения концов отрезка [a, b] в векторной форме Д  Формулы для определения начала и конца отрезка и определения значения f(x) в середине отрезка.  Р 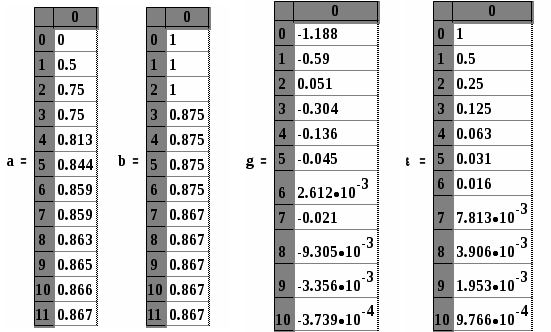 езультаты вычислений. З К Задачи для самостоятельного решения. Методом бисекции (половинного деления) уточнить корень уравнения. x3+x-1000=0 с точностью до 10-4. tg(x)=x на отрезке Практическая работа №7Численное решение нелинейных уравнений в Mathcad (метод Ньютона) Цель работы:научиться решать нелинейное уравнение в Mathcad, используя вычислительный алгоритм метода Ньютона (метод касательных). Задание №1. Решить нелинейное уравнение методом Ньютона. Знаменитый метод Ньютона является одним из наиболее эффективных способов численного решения нелинейных уравнений. Этот метод состоит в следующем. Пусть дано уравнение f(x)=0, (1) где f(x) непрерывная функция, требуется определить вещественные корни этого уравнения с точностью ε. Расчетная формула метода Ньютона имеет следующий вид  (2) (2)Выберем каким-либо способом, например, графически, приближенное значение корня x0 и, подставляя его в правую часть уравнения (2), можем начать итерационный процесс вычисления корня уравнения. Условием завершения итерационного процесса является выполнение условия В случае выполнения неравенства (3), корнем уравнения (1) будем считать значение xk+1. Рассмотрим реализацию алгоритма метода Ньютона в Mathcad на следующем примере. Найти действительные корни уравненияс точностью до трех значащих цифр. Установим формат чисел так, чтобы результаты вычислений отображались с нужным количеством знаков после десятичной точки (запятой). Преобразуем заданное уравнение к виду (1) и определим его правую часть как функцию f(x). Определим приближенное значение корня уравнения графически. Для этого построим график функции Определим начальное значение для вычислений следующим образом: x0:a. Определим дискретный аргумент k:=0..9, задающий количество итераций (вычисляемых значений xk). Определим первую производную функции f(x) как функцию d(x): Определим вычислительную формулу Ньютона в векторной форме: 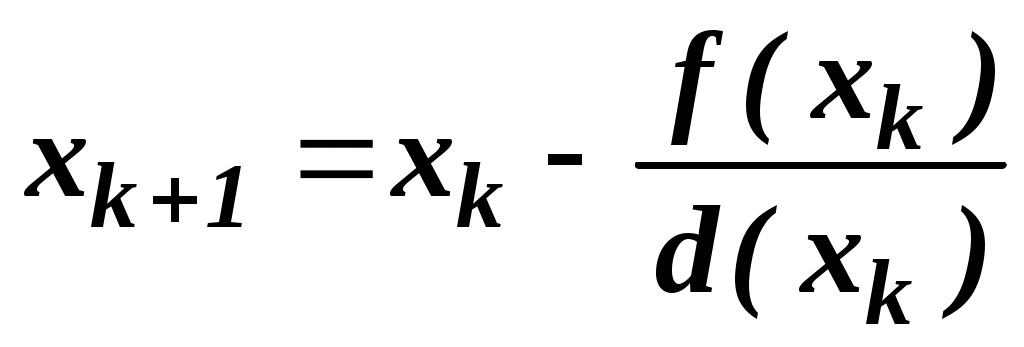 Для получения вектора результатов в свободном месте рабочего пространства Mathcad напишите: x=. Введите условие оценки погрешности вычислений Результат на экране: Нелинейное уравнение определено в виде функции. Локализация корней уравнения графическим способом. 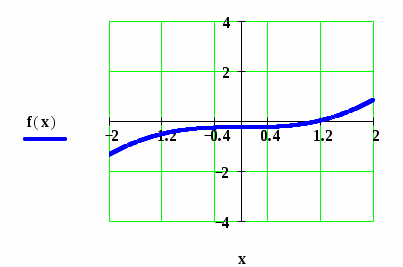 Приближенное значения корня уравнения. К Н 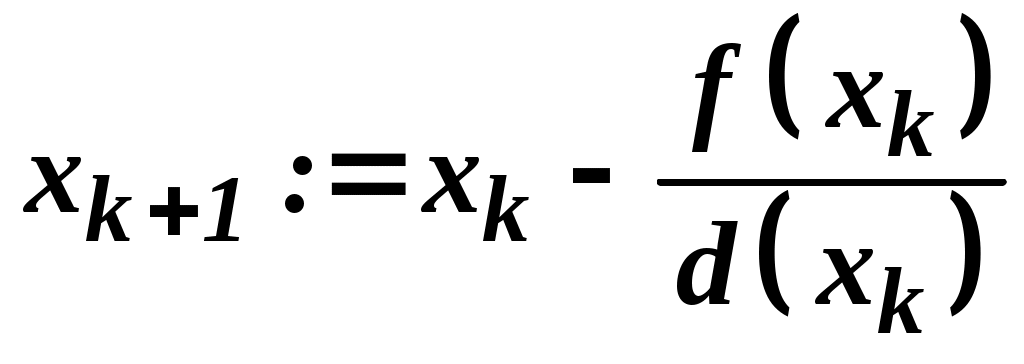 Вычислительная формула Ньютона. Результат вычислений. Расчет погрешности вычислений.   Погрешность вычислений становится допустимой на второй итерации Задачи для самостоятельного решения. Используя метод Ньютона, найти с точностью ε=10-6 положительный корень уравнений |
