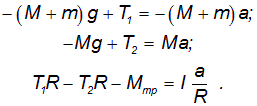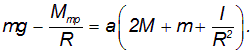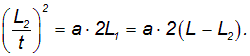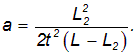Лабораторные работы (1) (2). Варианты к лабораторной работе (номер варианта соответствует первой букве вашей фамилии)
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
|
ВАРИАНТЫ К ЛАБОРАТОРНОЙ РАБОТЕ № 1. (номер варианта соответствует первой букве вашей фамилии)
Теоретические основы работыОсновные законы динамики материальных точек – это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:
называют основным уравнением динамики. Эскиз машины Атвуда показан на рис. 1. 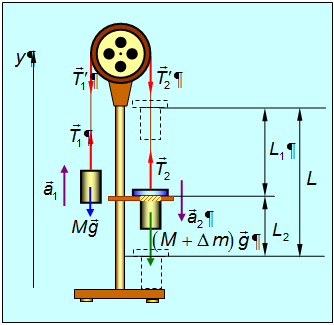 Рис. 1. Эскиз машины Атвуда Два одинаковых груза с массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m (в виде шайбы), то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на соответствующий груз с силой натяжения Т1 или Т2, а на блок – с силами Т’1 и Т’2. Тогда на каждый груз действует сила тяжести и сила натяжения нити. Основное уравнение динамики для груза с перегрузком имеет вид:
а для другого груза (без перегрузка):
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
где ΣMk – алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I – момент инерции блока относительно оси вращения; ε - его угловое ускорение. Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим
где: R – радиус блока; Мтр – момент силы трения. Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока: или
Проецируя уравнения (2) и (3) на ось у, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4а):
Умножая первое из уравнений (8) на (-1), и складывая все уравнения (8), получим
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m:
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11). Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы: 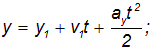 где у1, v1 – начальные параметры. Исключая из этих уравнений время t, при условии v1=0, получим
Система грузов перемещается на величину sy=L1, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12). В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину L2 за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу получим
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным. С помощью формулы (15) найдём расчётную формулу для величины ускорения а грузов с перегрузком:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||