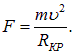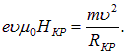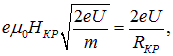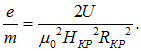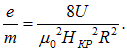Лабораторные работы (1) (2). Варианты к лабораторной работе (номер варианта соответствует первой букве вашей фамилии)
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
Теоретические основы работы
При движении электрона в поперечных электрическом или магнитном полях возможно определение удельного заряда по отклонению его траектории от первоначального направления. Электрическое поле с напряженностью Е действует на электрон, находящийся в этом поле с силой: где e=‑1.60219∙10-l9 Кл – заряд электрона. Здесь приведено табличное значение заряда электрона, которое определено в настоящее время с точностью до 5 знака после запятой. Заметим, что модуль заряда электрона называют элементарным зарядом. Направление этой силы противоположно направлению вектора напряженности электрического поля. Работа, совершаемая этой силой при движении электрона в поле, будет сопровождаться изменением кинетической энергии электрона. Магнитное поле с индукциейВ действует на электрон, движущийся в этом поле с силой Fm, силой Лоренца, которая зависит от величины и направления скорости движения электрона (рис. 1). 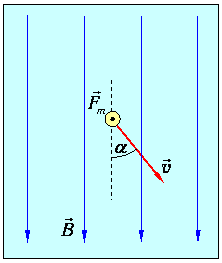 Рис. 1. Сила магнитного поля – сила Лоренца – равна;
где е – заряд электрона, v – скорость электрона, B – индукция магнитного поля. Если движение электрона происходит в вакууме (воздухе), то эту силу можно выразить через напряженность магнитного поля Н.
где а – угол между вектором напряженности поля и вектором скорости электрона, μ0=12.57-10' Гн/м – магнитная постоянная, μ – магнитная проницаемость среды (для вакуума или воздуха равна 1). Сила Лоренца перпендикулярна плоскости, в которой лежат векторы v и B. Направление ее можно определить по известному правилу «левой руки». Здесь надо учесть, что заряд электрона отрицателен. На рис. 1 направление силы показано точкой от плоскости чертежа на нас. Так как сила Лоренца перпендикулярна вектору скорости частицы, то она может изменить не величину, а только направление скорости электрона. В случае движения электрона по направлению линий индукции магнитного поля (sina=0) магнитная сила Fm=0, а при движении перпендикулярно к ним (sina=l) эта сила имеет максимальное значение и вызывает движение электрона по окружности (рис. 2). 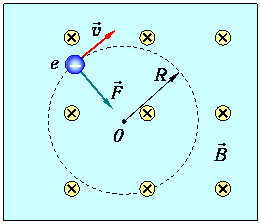 Рис. 2. Если в пространстве, где движется электрон, имеются одновременно электрическое и магнитное поля, то в общем случае будет происходить изменение скорости электрона как по величине, так и по направлению. Представим себе находящиеся в вакууме металлический цилиндр и металлическую накаливаемую нить, натянутую вдоль оси цилиндра (рис. 3). Если между нитью и цилиндром приложить разность потенциалов так, чтобы нить являлась катодом, а цилиндр положительным анодом, то электроны, вылетающие из нити, будут под действием электрического поля притягиваться к цилиндрическому аноду. Их движение будет прямолинейным и ускоренным. Если дополнительно создать внутри цилиндра однородное магнитное поле, напряженность которого параллельна оси цилиндра, то вылетающие из нити электроны, пересекая магнитное поле, будут двигаться не по радиальным, а по криволинейным траекториям. 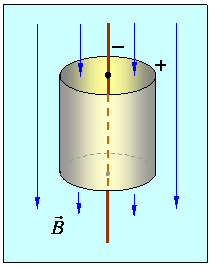 Рис. 3. Очевидно, что искривление траекторий электронов будет тем больше, чем больше будет действующая на них сила Лоренца, пропорциональная напряженности магнитного поля. Практически такую установку можно осуществить, поместив электронную лампу с цилиндрическим анодом в соленоид с током. Нагревая катод и создавая некоторую разность потенциалов U между катодом и анодом, будем пропускать через соленоид постоянный ток, получая тем самым постоянное магнитное поле внутри цилиндра-анода. Тогда на электрон, вылетевший из катода, одновременно будут действовать силы со стороны электрического и магнитного полей. Электрическая сила Fв направлена по радиусу от катода к аноду. Напряженность электрического поля в пространстве между двумя коаксиальными цилиндрами (катодом и анодом), строго говоря, переменна и определяется достаточно сложным выражением, которое мы приводить не будем. Однако приближенный анализ возможен из энергетических соображений. Электрон, пролетевший от катода к аноду, приобретает кинетическую энергию, равную работе электрической силы независимо от того, движется ли он по прямой или по любой другой траектории:
Таким образом, действие электрического поля между катодом и анодом сводится к разгону электрона до скорости v. Точный расчёт движения электрона в рассматриваемом (переменном с расстоянием) электрическом поле достаточно сложен, поэтому в дальнейшем будем приближённо считать, что электрон движется от катода к аноду с постоянной скоростью порядка v, где значение vопределяется формулой (3). Проводимый приближённый анализ не повлияет на верность получаемых в работе качественных результатов. Сила, действующая со стороны магнитного поля, зависит от напряженности магнитного поля Н внутри соленоида с током. Если соленоид достаточно длинный, то напряженность рассчитывается следующим образом:
где I – сила тока в соленоиде, N – число витков в соленоиде, 1 – длина соленоида. Магнитное поле искривляет траекторию движения электрона в плоскости, перпендикулярной оси катода и анода (предполагаем, что вылетающие из катода электроны не имеют скорости в направлении оси катода и анода, в противном случае, траектории электронов были бы спиральными). Очевидно, если Н мало, то траектории частиц будут слабо искривлены, и все электроны будут попадать на внутреннюю поверхность анода. Однако можно создать поле с такой напряженностью, что траектории электронов не пересекут поверхности анода, а все электроны вернутся на катод (рис. 4). 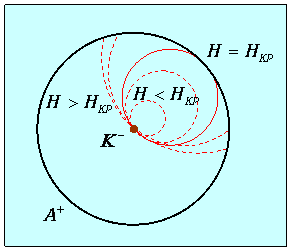 Рис. 4. Предельное значение напряженности магнитного поля: при котором прекращается попадание электронов на анод: называется критическим HКР. При напряженности HКР траектория электрона будет в рассматриваемом приближении круговой с радиусом RКР:который и будет определять нормальное (центростремительное) ускорение, приобретенное электроном под действием магнитной силы:
Тогда на основании (2) и (3) можно записать
Учитывая, что величина скорости определяется только электрическим полем (3), получим:
Откуда и получаем удельный заряд электрона:
Как видно из рис. 4. при величине поля Н=НКР радиус траектории электрона приближённо равен половине радиуса анода RКР,=0.5R.Тогда удельный заряд электрона равен
|