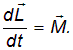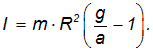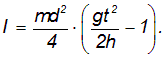Лабораторные работы (1) (2). Варианты к лабораторной работе (номер варианта соответствует первой букве вашей фамилии)

• Название: Варианты к лабораторной работе (номер варианта соответствует первой букве вашей фамилии)
• Дата: 09.04.2021
• Размер: 1.17 Mb.
• Имя файла: Лабораторные работы (1) (2).doc
• Тип: Исследование; #192940
• страница: 3 из 10

Теоретические основы работы

Маятник Максвелла представляет собой (рис. 1) массивный диск 2, закрепленный на оси 3, подвешенный на бифилярном подвесе.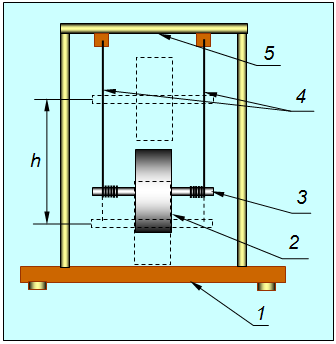



Рис. 1. Схема маятника Максвелла

Движение маятника (диска) Максвелла описывается следующей системой уравнений, справедливых для любого твердого тела:

		(1)
		(2)

Первое из уравнений описывает поступательное движение центра масс тела под действием приложенных к телу внешних сил, результирующая которых записана в правой части уравнения (1). Второе уравнение называется уравнением моментов и может быть записано относительно произвольного начала (как неподвижного, так и движущегося). Запись уравнения (2) относительно неподвижного начала может оказаться весьма неудобной, так как законы движения точек приложения сил, вызывающих моменты, до решения системы (1)-(2) неизвестны. Поэтому начало, относительно которого считаются моменты, удобно жестко связать с движущимся телом, то есть выбрать начало в системе отсчета, движущейся вместе с телом (с центром масс тела). Но центр масс тела движется ускоренно, вследствие чего связанная с ним система отсчета неинерциальна. Поэтому при произвольном выборе начала (жестко связанного с движущимся телом) в правой части уравнения (2) должны, появиться в качестве слагаемых моменты сил инерции (появление которых связано с движущейся системой отсчета). Однако, если в качестве начала выбрать сам центр масс тела, то суммарный момент сил инерции (относительно центра масс) обратиться в нуль. Тогда в правой части уравнения (2) под М понимается суммарный момент относительно центра масс всех внешних сил, действующих на тело, а под L в левой части - момент импульса твердого тела при его вращении относительно оси, проходящей через центр масс маятника, то есть относительно оси симметрии маятника.

Так как движение маятника Максвелла - плоское (каждая точка маятника движется в вертикальной плоскости), то второе уравнение упрощается и принимает вид

(3)

где L - проекция момента импульса, а M - проекция момента внешних сил на ось симметрии (ось вращения) маятника.

При вращении тела относительно оси, не меняющей своего направления, в частности, при вращении маятника вокруг оси симметрии, имеет место соотношение

(4)

где I - момент инерции тела относительно упомянутой оси, ω - угловая скорость вращения относительно этой же оси. На основании (3), (4) можно записать

		(5)
		(5а)

В последней формуле ε представляет собой угловое ускорение вращающегося тела.

Так как центр масс маятника движется вдоль вертикали (поднимается или опускается), то уравнение (1) также упрощается

		(6)
		(6а)

где а - означает проекцию ускорения тела, а F - проекцию суммы внешних сил на вертикальное направление.

Таким образом, система уравнений (1) - (2) принимает вид





Решая эти уравнения, можно определить закон движения маятника. Если же ускорение маятника известно, то можно найти момент инерции маятника относительно его оси. Ось симметрии мятника, относительно которой происходит его вращение, названа нами просто осью маятника. Нахождение момента инерции маятника и является целью настоящей работы, когда по измеряемым величинам вычисляется ускорение, а после чего находится момент инерции I.

Внешними силами, действующими на маятник, является сила тяжести mg и суммарная сила натяжения нитей Т (рис. 2).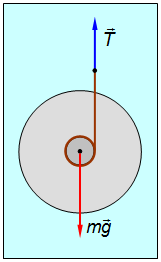



Рис. 2. Силы, действующие на маятник Максвелла

Принимая за положительное направление вертикали направление вниз, можно переписать уравнение (6) в виде:

(7)

Относительно оси маятника отличным от нуля моментом обладает только сила натяжения нити

(8)

где R - половина внешнего диаметра d оси маятника – стержня, на который наматывается нить (толщиной намотанной нити пренебрегаем). С учетом (8) уравнение (5) принимает вид

(9)

В отсутствие проскальзывания нити, cвязь между угловым ускорением ε маятника и ускорением a его центра масс имеет вид:

(10)

Исключая T и ε из уравнений (7), (9), (10), можно получить

(11)

Так как движение маятника вниз - равноускоренное, то

(12)

где h – первоначальная высота подъема маятника, а t – время опускания (падения) маятника Максвелла. Подстановка (12) в (11) позволяет получить окончательную расчётную формулу

(13)

Кинетическая энергия плоского движения твердого тела равна:



где v – скорость центра масс, I – момент инерции тела относительно оси, проходящей через его центр масс. Пренебрегая силами сопротивления, можно было бы получить нашу расчётную формулу (13) и с помощью закона сохранения механической энергии, приравнивая механические энергии маятника в начальном и конечном положениях, например, для движения вниз



и, учитывая, что в отсутствие проскальзывания нити, линейная скорость движения связана с угловой скоростью известной формулой



а также то, что для равноускоренного движения маятника вниз высота h связана с конечной скоростью v формулой