Лабораторные работы (1) (2). Варианты к лабораторной работе (номер варианта соответствует первой букве вашей фамилии)
 Скачать 1.17 Mb.
|
Обработка экспериментальных данныхПравила записи результатов измерений При записи результата измерений в стандартной форме (А =<А> ± ∆А, где <А> – среднее значение физической величины, ∆А – абсолютная погрешность физической величины) необходимо соблюдать следующие правила: 1. погрешность ∆А необходимо округлить до двух значащих цифр, если первая из них – единица, и до одной значащей цифры во всех остальных случаях; 2. при записи значения <А> необходимо указывать все цифры вплоть до последнего десятичного разряда, использованного для записи погрешности Понятие знaчaщей и незнaчaщей цифры Будем называть значащими цифрами верные и сомнительную цифры числа. Незначащими цифрами являются: 1) нули в начале числа, при помощи которых определяются разряды десятичных дробей в числах, меньших единицы; 2) нули в конце числа, заменяющие после округления отброшенные (неверные или вообще неизвестные) цифры; 3) неверные цифры, если они почему-либо не отброшены. Значащие цифры данного числа – все цифры от первой слева, не равной нулю, до последней справа. При этом нули, следующие из множителя 10k (k – целое число), не учитывают. Примеры: 1) 0,2396 – 4 значащие цифры, первая цифра – 2; 2) 0,00173 – 3 значащие цифры, первая цифра – 1; 3) 30170 – 5 значащих цифр, первая цифра – 3, последний нуль – также значащая цифра; 4) 301,7·102 – 4 значащие –цифры, первая цифра – 3, последняя – 7; 5) 20000 – 5 значащих цифр, первая цифра – 2, все последующие нули –также значащие цифры; 6) 20·103 – 2 значащие цифры, первая цифра – 2, вторая цифра – 0, нули, следующие из множителя 103, не учитывают; 7) 0,02·106– одна и единственная значащая цифра – 2. Пример. Обработка результатов прямых измерений диаметра d шарика с помощью микрометра. Значения diдля пяти измерений приведены во втором столбце таблицы.
Проводим расчеты:  Полагая стандартную инструментальную погрешность микрометра равной его точности (  ), найдем стандартную погрешность диаметра шарика: Правильная запись результата измерений:  Примеры неправильной записи результата измерений: 1)  – погрешность занижена больше, чем на 15=20 % из-за нарушения правила 1;2)  – нарушено правило 2;3)  – не выполнено правило 1Компьютерная модель имитирует опыт, данные которого необходимо записать. Затем полученные значения обработать по предложенной методике и представить конечный результат с необходимым количеством значащих цифр. Особенность заданий в том, что погрешности практически отсутствуют, что значительно облегчает расчеты. Однако «лишние» цифры (незначащие) могут возникнуть в результате расчетов, поэтому важно уметь округлять конечный результат так, чтобы в нем оставались только верные цифры. Количество верных цифр определяется шкалой и пределом измерений приборов. Но в промежуточных расчетах нужно оставлять цифры «с запасом»: к верным цифрам нужно добавлять сомнительную цифру. Также важно уметь записывать числа в стандартной форме (  ) с указанием единиц измерения.Правила построения графиков Результаты экспериментов обычно представляют не только в виде таблиц, но и в графической форме. Для графиков следует использовать специальную бумагу (миллиметровую, логарифмическую или полулогарифмическую). Перед построением графика следует исходя из пределов, в которых заключены значения функции и аргумента, выбрать разумные масштабы по оси абсцисс и по оси ординат. Эти масштабы выбираются произвольно, независимо друг от друга, но так, чтобы экспериментальные точки заняли всю площадь графика. Иногда интервал, в котором заключены значения аргумента или функции, лежит далеко от нуля. В этом случае целесообразно начинать деления на соответствующей оси не с нуля, а с некоторого значения, лишь немногим меньшего, чем наименьшее значение, которое надо отложить на этой оси. В противном случае на графике получается много свободного места, а сама кривая – в очень мелком масштабе (рис. 1а). Масштабные деления наносят на оси, около них пишут соответствующие цифры. Стрелками указывают направления, в которых возрастают откладываемые величины. У концов осей пишут обозначения этих величин с указанием единиц измерения. Проводить перпендикуляры от точек к осям координат не следует, так как они загромождают рисунок и мешают анализировать результаты. Через экспериментальные точки всегда следует проводить самую простую кривую, совместимую с этими точками, т.е. кривую, от которой экспериментальные данные отступают, как правило, не более чем на стандартную ошибку. Эта кривая должна быть плавной и проходить таким образом, чтобы примерно одинаковое число точек находилось бы над кривой и под ней. Для проведения на графиках кривых линий пользуются лекалами. 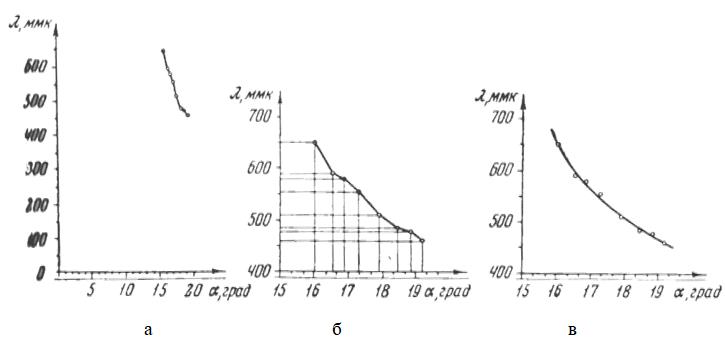 Рис 1. Примеры неправильного (а и б) и правильного (в) построения графиков. Проведение наилучшей прямой Существуют различные методы проведения прямых линий через экспериментальные точки. Самый простой способ, пригодный для оценки результатов, состоит в использовании прозрачной линейки. Благодаря прозрачности линейки видно, сколько точек находится по обе стороны от проводимой линии. Её надо провести так, чтобы по обе стороны было одинаковое количество экспериментальных точек. Параметры этой линии (наклон, пересечения с осями координат) измеряются непосредственно на графике. В результате получаем аналитическое выражение прямой 𝑦 = 𝑎 + 𝑏𝑥, которая в общем случае при 𝑎, не равном нулю, не проходит через начало координат. Рекомендации по оформлению отчета1. Отчет оформляют в электронном виде в редакторе Word 2. Объем отчета составляет 2-3 страницы. 3. В отчете необходимо указать: 3.1 Фамилию, имя, отчество студента; 3.2 Номер группы; 3.3 Дисциплину; 3.4 Фамилию, имя, отчество преподавателя; 4. Рекомендуемая структура отчета: 4.1 Название работы; 4.2 Цель работы; 4.3 Таблицы измерений и таблицы расчетов 4.5 Формулы и законы, используемые для расчетов; 4.6 Подстановка значений величин в формулы и результаты расчетов; 4.7 Результаты ускорения а и ускорения свободного падения g в стандартной форме |