Лінійна алгебра та аналітична геометрія. Матриці і визначники Матриця. Основні визначення. Лінійні операції над матрицями
 Скачать 52.36 Kb. Скачать 52.36 Kb.
|
Матрицею 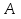 розміром розміром 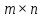 називають прямокутну таблицю чисел, розташованих у називають прямокутну таблицю чисел, розташованих у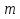 рядках та рядках та 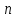 стовпцях, і позначають великими літерами латини і беруть у круглі ( ), квадратні [ ] або подвійні || || дужки: стовпцях, і позначають великими літерами латини і беруть у круглі ( ), квадратні [ ] або подвійні || || дужки: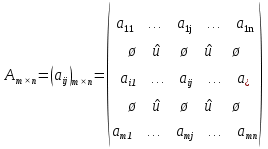 . .
Числа 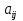 , , 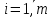 , , 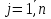 , називаються елементами матриці , називаються елементами матриці 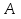 . . Елементами матриці називаються елементи таблиці чисел, з яких вона складається.
Число 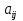 . .Приклад. Матриця 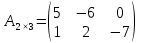 має 2 рядка та 3 стовпці. Елемент має 2 рядка та 3 стовпці. Елемент 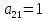 знаходиться у 2-му рядку та 1-му стовпці. знаходиться у 2-му рядку та 1-му стовпці.
Матриця називається квадратною, якщо кількість стовпців цієї матриці дорівнює кількості її рядків, тобто 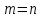 . . Квадратну матрицю розміру 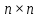 називають матрицею порядку називають матрицею порядку 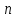 та позначають: та позначають: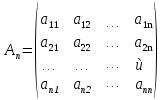 . .Числа 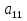 , , 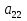 ,…, ,…, 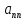 утворюють головну діагональ квадратної матриці утворюють головну діагональ квадратної матриці 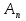 , а , а 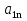 , , 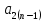 ,…, ,…, 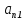 числа утворюють побічну діагональ матриці числа утворюють побічну діагональ матриці 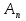 . .Квадратна матриця називається верхньою трикутною (нижньою трикутною), якщо всі її елементи нижче (вище) головної діагоналі, рівні нулю. Приклад. Матриця 4-го порядку 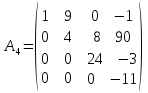 є верхньою трикутною матрицею, а матриця є верхньою трикутною матрицею, а матриця 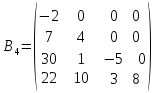 є нижньою трикутною матрицею. є нижньою трикутною матрицею.
Порядком квадратної матриці називається число її рядків (стовпців).
Матриця називається нульовою, якщо всі її елементи дорівнюють нулю. Позначається 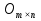 . .Приклад. Нульова матриця 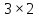 : : 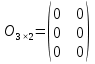 . .
Квадратна матриця називається діагональною, якщо всі її елементи окрім елементів головної діагоналі дорівнюють нулю. Приклад. Діагональна матриця третього порядку: 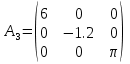 . .
Діагональна матриця називається одиничною, якщо всі елементи головної діагоналі цієї матриці дорівнюють одиниці. Одиничні матриці позначаються літерами 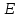 або або 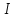 . .Приклад. Одинична матриця порядку 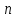 : : 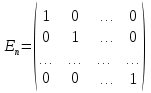 . .Матриця, яка містить один рядок (стовпець), називається матрицею-рядком або вектор-рядком (матрицею-стовпцем або вектор-стовпцем). Приклад. Матриця 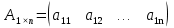 є матрицею-рядком, що містить є матрицею-рядком, що містить 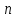 елементів, а матриця елементів, а матриця 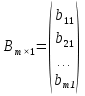 є матрицею-стовпцем, що містить є матрицею-стовпцем, що містить 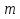 елементів. елементів.Яка матриця називається східчастою?Матриця 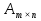 називається східчастою, якщо крайній елемент кожного рядка знаходиться справа від крайнього елемента попереднього рядка. називається східчастою, якщо крайній елемент кожного рядка знаходиться справа від крайнього елемента попереднього рядка.Елемент рядка матриці 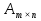 називається крайнім, якщо він відмінний від нуля, а всі елементи цього рядка, які знаходяться зліва від нього, дорівнюють нулю. називається крайнім, якщо він відмінний від нуля, а всі елементи цього рядка, які знаходяться зліва від нього, дорівнюють нулю.Приклад. Східчаста матриця розміру 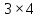 : : 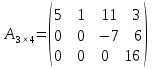 . .Елементи 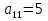 , , 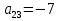 та та 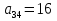 є крайніми елементами 1-го, 2-го та 3-го рядків відповідно. є крайніми елементами 1-го, 2-го та 3-го рядків відповідно.
Матриці 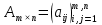 та та 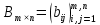 називаються рівними між собою, якщо вони однакової розмірності і всі відповідні елементи цих матриць рівні між собою. називаються рівними між собою, якщо вони однакової розмірності і всі відповідні елементи цих матриць рівні між собою.
Сумою матриць однакової розмірності 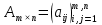 та та 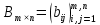 називається матриця називається матриця 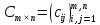 , кожен елемент якої дорівнює сумі відповідних елементів матриць , кожен елемент якої дорівнює сумі відповідних елементів матриць 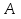 та та 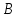 , тобто , тобто 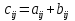 , , 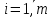 , , 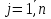 . Позначається : . Позначається : 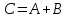 . .Приклад. Задано матриці: 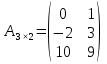 та та 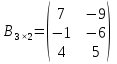 . . Тоді 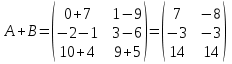 . .
Ні.
Сумою 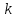 матриць називається матриця, яка є результатом послідовного додавання даних матриць. матриць називається матриця, яка є результатом послідовного додавання даних матриць.
Добутком матриці 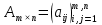 на число на число 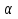 називається матриця називається матриця 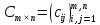 , кожен елемент якої дорівнює добутку кожного елемента матриці , кожен елемент якої дорівнює добутку кожного елемента матриці 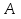 на число на число 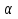 , тобто , тобто 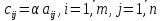 . .Приклад. Для матриці 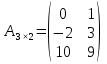 та числа та числа 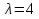 : : 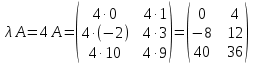 . .
Матриця 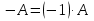 називається протилежною до матриці називається протилежною до матриці 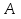 . .
Різницею матриць однакової розмірності 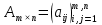 та та 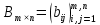 називається матриця називається матриця 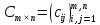 , кожен елемент якої дорівнює різниці відповідних елементів матриць , кожен елемент якої дорівнює різниці відповідних елементів матриць 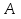 та та 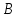 , тобто , тобто 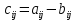 , , 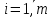 , , 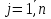 . Позначається : . Позначається : 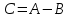 . .Приклад. Задано матриці: 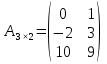 та та 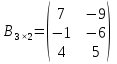 . . Тоді 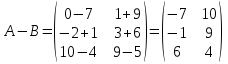 . .
Лінійними операціями над матрицями називаються додавання матриць і множення матриці на число.
Основні властивості операцій додавання матриць та множення матриці на число: Теорема. Для довільних матриць 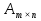 , , 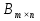 , , 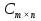 , та чисел , та чисел 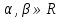 виконується: виконується:
Доведення. Всі властивості операцій додавання матриць та множення на число випливають безпосередньо з означень цих операцій та властивостей операцій додавання дійсних чисел.
Задано матриці: 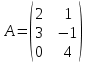 ; ; 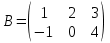 ; ; 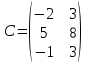 ; ; 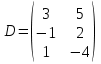 . .Матрицю 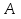 не можна додавати до матриці не можна додавати до матриці 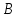 , оскільки матриця , оскільки матриця 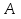 має розміри має розміри 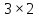 , а матриця , а матриця 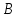 - розміри - розміри 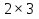 , а додавати можливо лише матриці однакової розмірності. , а додавати можливо лише матриці однакової розмірності.Матриці 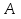 і і 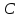 однакової розмірності, тому додати їх можливо: однакової розмірності, тому додати їх можливо: 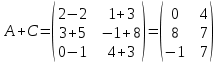 . .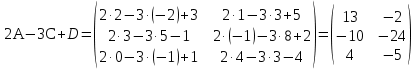 . .
а) 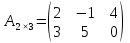 ; б) ; б) 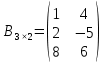 ; в) ; в) 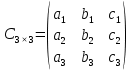 . .
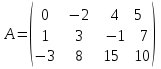 : : 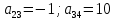 . .
Матриця 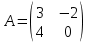 є квадратною з порядком 2; є квадратною з порядком 2;матриця 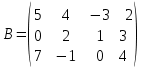 не є квадратною; не є квадратною;матриця 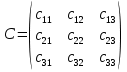 є квадратною з порядком 3. є квадратною з порядком 3.
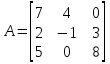 : :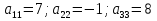 – елементи складають головну діагональ; – елементи складають головну діагональ;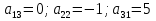 – елементи складають побічну діагональ. – елементи складають побічну діагональ.
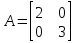 є діагональною, тому що всі елементи матриці, окрім головної діагоналі, дорувнюють нулю; є діагональною, тому що всі елементи матриці, окрім головної діагоналі, дорувнюють нулю;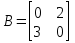 не є діагональною; не є діагональною;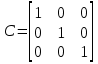 є діагональною, тому що всі елементи матриці, окрім головної діагоналі, дорувнюють нулю. є діагональною, тому що всі елементи матриці, окрім головної діагоналі, дорувнюють нулю.
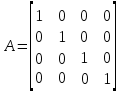 . .
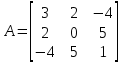 є симетричною матрицею; є симетричною матрицею;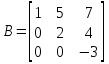 є верхньою трикутною матрицею, оскільки всі елементи її нижче від головної діагоналі дорівнюють нулю; трапецевидна; є верхньою трикутною матрицею, оскільки всі елементи її нижче від головної діагоналі дорівнюють нулю; трапецевидна;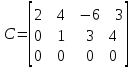 є трапецевидною матрицею; є трапецевидною матрицею;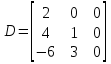 є нижньою трикутною матрицею, оскільки всі елементи її вище від головної діагоналі дорівнюють нулю; є нижньою трикутною матрицею, оскільки всі елементи її вище від головної діагоналі дорівнюють нулю;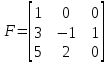 . .
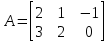 та та 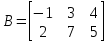 : : 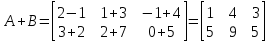 . .
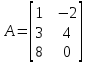 : : 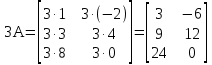 ; ; 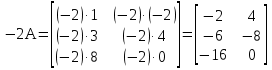 . .
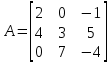 ; ; 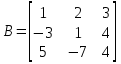 ; ; 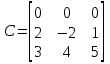 : :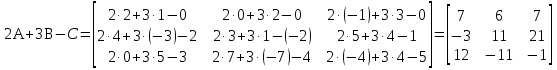 ; ;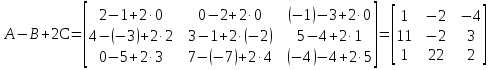 . .
а) 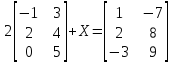 : : 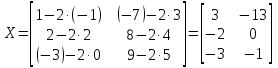 ; ;б) 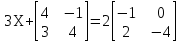 : : 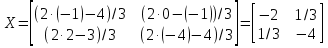 . . |

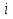 -му рядку та
-му рядку та 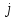 -му стовпці матриці
-му стовпці матриці 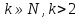 ?
?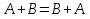 ;
;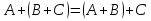 ;
;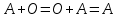 ;
;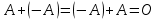 ;
;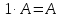 ;
;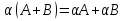 ;
;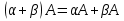 ;
;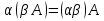 .
.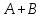 ,
, 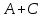 ? Знайти
? Знайти 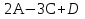 .
.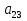 ,
, 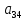 , якщо
, якщо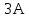 та
та 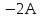 :
: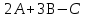 та
та 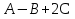 :
: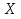 .
.