prakticheskaya_rabota_Матрицы. Операции над матрицами. Матрицы. Операции над матрицами
 Скачать 136.38 Kb. Скачать 136.38 Kb.
|
|
Практическая работа №1 Тема: Матрицы. Операции над матрицами. Цель: сформировать умение выполнять основные операции над матрицами. Теоретические сведения к практической работе Определение. Матрицей размером nm называется прямоугольная таблица, составленная из n m чисел и имеющая n строк и m столбцов. Числа ij, составляющие матрицу, называются элементами матрицы А=(ij)=  Определение. Матрицу Аt называют транспонированной по отношению к матрице А, если она получена из матрицы А заменой строк этой матрицы её столбцами, и, наоборот, столбцов строками. 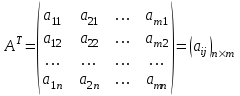 . .Пример,  , , 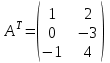 . . Определение. Квадратная матрица называется треугольной, если все ее элементы, размещенные над главной диагональю (под ней), равны нулю, т.е. 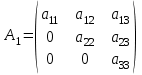 - верхняя треугольная матрица, - верхняя треугольная матрица,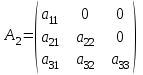 – нижняя треугольная матрица. – нижняя треугольная матрица.Определение. Матрица, все элементы которой равны нулю, называется нуль-матрицей. Матрица-строка 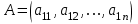 , матрица-столбец , матрица-столбец 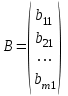 . .Операции над матрицами. 1) Пусть матрицы 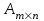 и и  одинаковой размерности. Суммой матриц одинаковой размерности. Суммой матриц 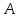 и и  называется матрица называется матрица 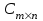 той же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы той же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы 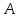 и и  . .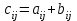 для всех для всех  и и 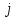 . .2) Разностью матриц 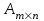 и и  одинаковой размерности называется матрица одинаковой размерности называется матрица 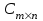 той же размерности, каждый элемент которой рамен разности соответствующих элементов матрицы той же размерности, каждый элемент которой рамен разности соответствующих элементов матрицы 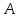 и и  . .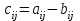 для всех для всех  и и 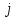 . .3) Произведением матриц 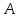 на число на число 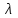 называется матрица называется матрица 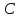 , каждый элемент которой равен , каждый элемент которой равен 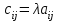 . .4) Матрицу 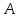 можно умножить на матрицу можно умножить на матрицу  ( ( ) лишь в то случае, когда число столбцов первой матрицы ) лишь в то случае, когда число столбцов первой матрицы 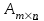 равно число строк второй матрицы равно число строк второй матрицы  , т.е. , т.е. 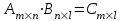 . При этом каждый элемент матрицы-произведения . При этом каждый элемент матрицы-произведения  определяется так: определяется так: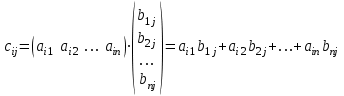 , для всех , для всех  и и 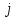 . .Т.е., элемент 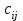 равен сумме произведений элементов равен сумме произведений элементов  -й строки матрицы -й строки матрицы 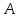 на соответствующие элементы на соответствующие элементы 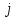 -го столбца матрицы -го столбца матрицы  . .Найти произведение матрицы-строки и матрицы-столбца: Пример 1. 1) 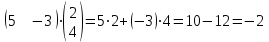 , ,2) 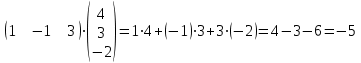 , ,3) 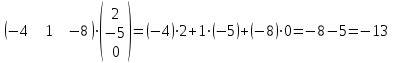 , ,4) 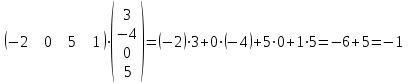 , ,5)   . .Пример 2 Для заданных матриц 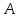 , ,  , , 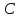 найти матрицы найти матрицы 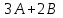 , , 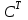 , , 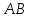 , , 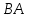 , , 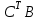 , , 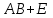 , ,  . . , , 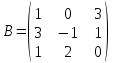 , ,  . .Решение 1.1) 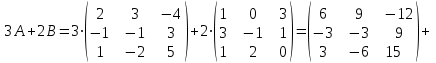 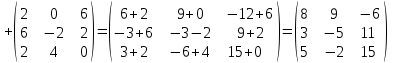 ; ;1.2) 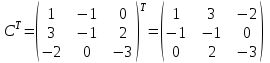 ; ;1.3) 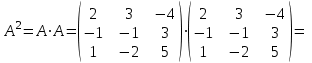 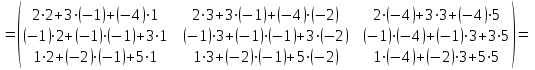 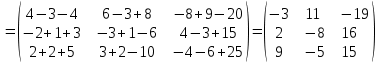 ; ;1.4)  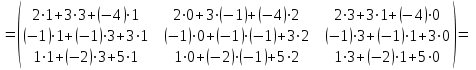 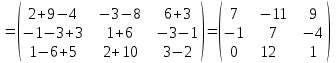 ; ;1.5)    . .Подчеркнем еще раз, что 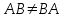 . .1.6) 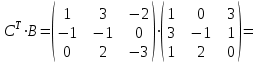 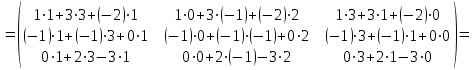 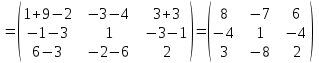 ; ;Содержание практической работы: Задание 1. Для матриц 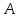 , ,  , , 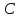 вычислить: вычислить:1) 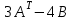 , 2) , 2) 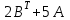 , 3) , 3)  , ,4) 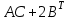 , 5) , 5) 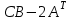 , 6) , 6)  , если , если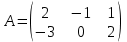 , , 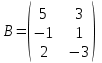 , ,  . .Задание 2. Для матриц 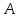 , ,  , , 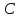 вычислить: вычислить:1) 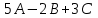 , 2) , 2) 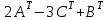 , ,3) 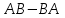 , 4) , 4) 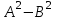 , если , если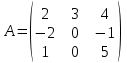 , , 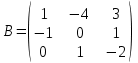 , , 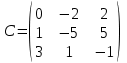 . .Задание 3. Найти произведение матриц: 1)  ; 2) ; 2) 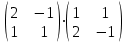 ; ;3) 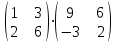 ; 4) ; 4) 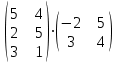 ; ;5) 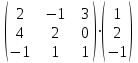 ; 6) ; 6)  ; ;7) 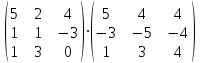 ; 8) ; 8) 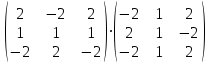 |
