ЛР№7. Маятник Обербека
 Скачать 99.72 Kb. Скачать 99.72 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Факультет компьютерных технологий и информатики отчет по лабораторной работе №7 по дисциплине «Физика» Тема: Маятник Обербека
Санкт-Петербург 2021 Цель работы. Экспериментальное исследование законов динамики вращательного движения твердого тела на примере маятника Обербека, определение постоянной части момента инерции маятника Обербека. Схема установки. Маятник Обербека (рис. 1) представляет собой крестовину 1 с грузами 2, на вращающейся оси 3. 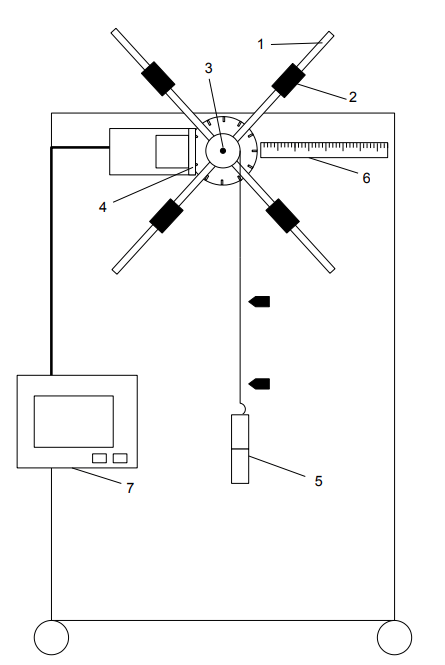 Рисунок 1 — Схема маятника Обербека На шкив на оси намотана нить с грузиком 5, которая, разматываясь, вызывает вращательное движение крестовины. На четырех взаимно перпендикулярных стержнях крестовины располагаются четыре подвижных груза 2 массой 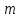 каждый, положение которых относительно оси вращения маятника определяется по измерительной линейке 6. В опыте положения грузов на крестовине меняют с помощью их перемещения по резьбовым спицам крестовины. Фиксация грузов в каждой серии измерений осуществляется путем законтривания двух резьбовых половин каждого груза в выбранном положении. На оси крестовины располагается датчик 4 угловой скорости вращения маятника, подключенный через концентратор к измерительному блоку 7. каждый, положение которых относительно оси вращения маятника определяется по измерительной линейке 6. В опыте положения грузов на крестовине меняют с помощью их перемещения по резьбовым спицам крестовины. Фиксация грузов в каждой серии измерений осуществляется путем законтривания двух резьбовых половин каждого груза в выбранном положении. На оси крестовины располагается датчик 4 угловой скорости вращения маятника, подключенный через концентратор к измерительному блоку 7.Основные теоретические положения. Вращение маятника описывается основным уравнением динамики вращательного движения 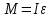 , (1) , (1)где 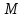 – момент сил, действующих на маятник; – момент сил, действующих на маятник;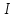 – его момент инерции. – его момент инерции.Вращательный момент М сил, действующих на маятник, определяется выражением: 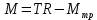 , (2) , (2)где 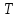 – сила, действующая на шкив маятника со стороны нити; – сила, действующая на шкив маятника со стороны нити;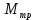 – момент сил трения в оси маятника; – момент сил трения в оси маятника;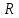 – радиус шкива, на который намотана нить с прикрепленным к ней грузом – радиус шкива, на который намотана нить с прикрепленным к ней грузом 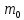 . .Движение груза 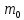 на нити описывается вторым законом Ньютона на нити описывается вторым законом Ньютона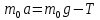 . (3) . (3)С учетом этого уравнения момент сил, действующих на маятник, можно записать в виде: 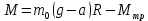 . (4) . (4)Если подставить (4) в (1), то уравнение вращательного движения маятника примет вид 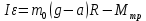 . (5) . (5)С учетом, что угловое ускорение 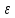 вращения маятника связано с ускорением вращения маятника связано с ускорением 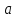 движения груза движения груза 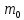 соотношением соотношением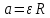 , (6) , (6)это уравнение можно привести к виду: 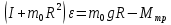 , (7) , (7)В этой формуле правая часть равенства есть постоянная величина. Отсюда следует, что вращение маятника для выбранного в опыте положения грузов является равноускоренным. Кроме того, из формулы (7) следует, что увеличение момента инерции 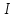 системы должно приводить в данной работе к уменьшению углового ускорения системы должно приводить в данной работе к уменьшению углового ускорения 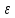 ее вращения, и наоборот. ее вращения, и наоборот.Если 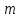 – масса одного из грузов на крестовине, – масса одного из грузов на крестовине, 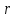 – его расстояние до оси вращения маятника, то момент инерции крестовины с 4-мя грузами в формуле (7) равен – его расстояние до оси вращения маятника, то момент инерции крестовины с 4-мя грузами в формуле (7) равен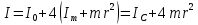 , (8) , (8)где 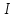 – суммарный момент инерции крестовины без грузов; – суммарный момент инерции крестовины без грузов;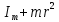 – момент инерции одного из подвижных грузов, рассчитанный по теореме Гюйгенса-Штейнера; – момент инерции одного из подвижных грузов, рассчитанный по теореме Гюйгенса-Штейнера;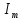 – его собственный момент инерции; – его собственный момент инерции;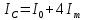 – постоянная часть момента инерции маятника Обербека. – постоянная часть момента инерции маятника Обербека.Момент инерции 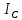 в данной работе является экспериментально определяемой величиной. Для его нахождения запишем (7) для двух различных положений в данной работе является экспериментально определяемой величиной. Для его нахождения запишем (7) для двух различных положений 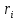 и и 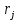 грузов грузов 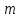 относительно оси вращения маятника: относительно оси вращения маятника: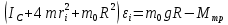 , (9) , (9)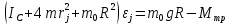 . (10) . (10)Равенство правых частей этих равенств означает и равенство их левых частей: 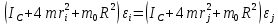 , (11) , (11)Отсюда можно найти искомую величину 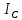 : :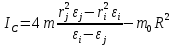 , (11) , (11)где 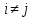 , и при , и при 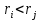 должно быть должно быть 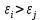 . .В этой формуле величины 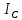 , , 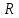 , , 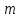 , , 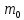 – константы, поэтому множитель – константы, поэтому множитель 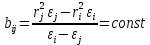 при различной геометрии постановки эксперимента. при различной геометрии постановки эксперимента.Угловое ускорение вращения маятника определяется по формуле 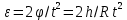 , где , где 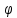 – угол поворота шкива при прохождении грузом на нити расстояния – угол поворота шкива при прохождении грузом на нити расстояния 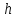 между двумя метками на установке за время между двумя метками на установке за время 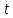 . Операцию определения времени . Операцию определения времени 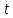 и вычисления и вычисления 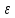 в работе выполняет измерительный блок установки. При этом средние значения в работе выполняет измерительный блок установки. При этом средние значения 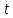 и и 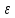 по четырем измерениям в одном опыте высвечиваются на ЖК дисплее установки. по четырем измерениям в одном опыте высвечиваются на ЖК дисплее установки.Обработка результатов эксперимента.
Используя данные таблицы 2, проверьте близость значений коэффициентов 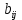 в формуле (11) при различной геометрии постановки эксперимента и, при их близости, рассчитайте постоянную часть момента инерции маятника Обербека в формуле (11) при различной геометрии постановки эксперимента и, при их близости, рассчитайте постоянную часть момента инерции маятника Обербека 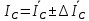 с с 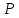 = 95%. = 95%.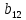 = 10,35 * 10-4 м2 = 10,35 * 10-4 м2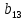 = 11,43 * 10-4 м2 = 11,43 * 10-4 м2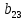 = 13,23 * 10-4 м2 = 13,23 * 10-4 м2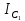 = 1,117 * 10-3 кг*м2 = 1,117 * 10-3 кг*м2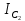 = 1,2466 * 10-3 кг*м2 = 1,2466 * 10-3 кг*м2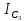 = 1,5838 * 10-3 кг*м2 = 1,5838 * 10-3 кг*м2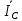 = 1,3158 * 10-3 кг*м2 = 1,3158 * 10-3 кг*м2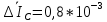 кг*м2 кг*м2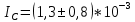 кг*м2 кг*м2Расчёт для двух опытов момента силы трения, действующего в оси маятника. В соответствии с формулами (9) и (10) получаем: 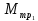 = = 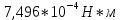 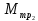 = = 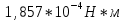 Из-за большой погрешности 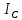 эти значения так различаются. эти значения так различаются.Расчёт момента инерции крестовины маятника Обербека. Исходя из формулы 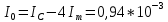 кг*м2. кг*м2.Расчёт по одной из серий Таблицы 7.2 в момент времени t угловой скорости вращения маятника, угла его поворота и числа сделанных им оборотов; линейной скорости, касательного, нормального и полного ускорения точек на ободе шкива. Определение пути, который прошёл груз на нити за это время. Сопоставление полученного значения со значением h в Таблице 1. Для расчета возьмем первую серию опытов. 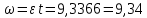 рад/c рад/c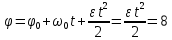 рад рад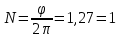 полный оборот полный оборот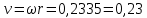 м/с м/с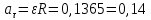 м/с2 м/с2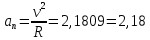 м/с2 м/с2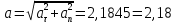 м/с2 м/с2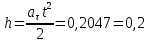 м, сходится с данными из таблицы. м, сходится с данными из таблицы.Выводы. Удалось экспериментально изучить законы динамики вращательного движения твёрдого тела на примере маятника Обербека и определить его постоянную часть момента инерции 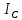 , момент сил трения в оси маятника, момент инерции крестовины, а также кинематические характеристики движения для одной из серии опытов. , момент сил трения в оси маятника, момент инерции крестовины, а также кинематические характеристики движения для одной из серии опытов.Протокол к л.р. №7 Таблица 1 – Параметры установки
Приборные погрешности масс 2 г, 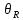 = 0.5 мм, = 0.5 мм, 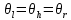 = 1 мм. = 1 мм.Таблица 2 – Результаты наблюдений
Выполнил: Жилин И.А. Факультет: КТИ Группа: № 1303 Проверила: Дедык А.И. 02.11.2021 Ответы на теоретические вопросы. Укажите на рисунке установки направление векторов момента силы и момента импульса во время движения груза вниз.         p L M r F 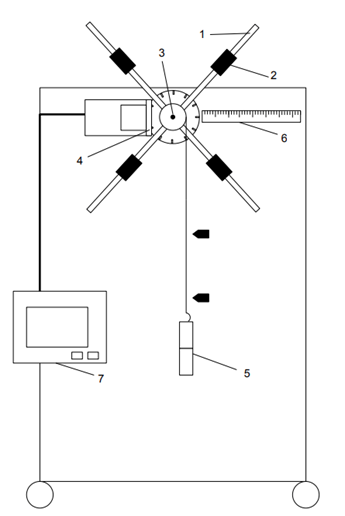 Рисунок 2 — Изображение момента силы и момента импульса на установке Момент силы M материальной точки относительно некоторого начала отсчёта определяется векторным произведением силы и её радиус-вектора до линии действия силы. Момент импульса L материальной точки определяется векторным произведением её радиус-вектора и импульса. Во время движения груза вниз направления векторов силы и импульса будут совпадать, таким образом векторы момента силы и момента импульса будут направлены вдоль оси вращения, а именно (по правилу буравчика) в направлении взгляда на схему на рисунке. Дайте определение момента инерции абсолютно твердого тела относительно некоторой оси. Как связан момент инерции с моментом импульса? Момент инерции – скалярная физическая величина, мера инертности во вращательном движении вокруг оси, равная сумме произведений масс всех материальных точек системы на квадраты их расстояний до оси. Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела 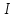 на угловую скорость на угловую скорость 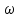 его вращения: его вращения: 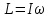 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

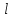 , см
, см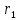 , см
, см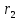 , см
, см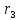 , см
, см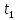 , с
, с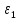 , с-2
, с-2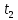 , с
, с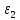 , с-2
, с-2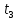 , с
, с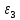 , с-2
, с-2