динамика. Динамика. Решение Момент инерции всего маятника Обербека равен сумме моментов инерции крестовины и всех четырёх грузов на спицах
 Скачать 61.06 Kb. Скачать 61.06 Kb.
|
|
6.46. Маятник Обербека состоит из крестовины, которая может вращаться вокруг горизонтальной оси. Крестовина имеет шкив, радиусом 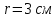 , на который наматывается нить. На спицах крестовины на расстоянии , на который наматывается нить. На спицах крестовины на расстоянии  от оси прикреплены четыре одинаковых груза, массой от оси прикреплены четыре одинаковых груза, массой  каждый. Определить момент инерции каждый. Определить момент инерции  крестовины, если груз массой крестовины, если груз массой 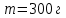 , привязанный к нити, опускается с высоты , привязанный к нити, опускается с высоты  за время за время  . Грузы считать материальными точками. . Грузы считать материальными точками.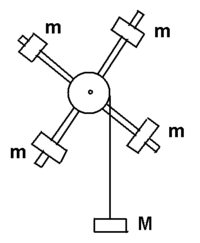
На шкив радиусом  действует момент силы натяжения нити действует момент силы натяжения нити 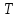 , плечо которой равно радиусу шкива, т.к. сила натяжения направлена по касательной к шкиву. , плечо которой равно радиусу шкива, т.к. сила натяжения направлена по касательной к шкиву. 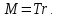 Момент силы натяжения нити сообщает всему маятнику некоторое угловое ускорение 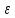 (второй закон Ньютона для вращательного движения маятника). (второй закон Ньютона для вращательного движения маятника).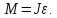 Натяжение нити создаётся весом груза 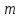 , привязанного к нити. По второму закону Ньютона для груза , привязанного к нити. По второму закону Ньютона для груза 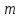 на нити, движущегося с ускорением на нити, движущегося с ускорением 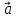 , на который по направлению движения действует сила тяжести , на который по направлению движения действует сила тяжести  , а против направления движения – сила натяжения нити , а против направления движения – сила натяжения нити 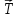 , в проекции на вертикаль: , в проекции на вертикаль: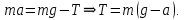 Ускорение  движения груза, равное тангенциальному ускорению движения точки касания нити к шкиву, пропорционально угловому ускорению маятника. движения груза, равное тангенциальному ускорению движения точки касания нити к шкиву, пропорционально угловому ускорению маятника.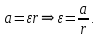 Второй закон Ньютона для вращательного движения маятника примет вид:  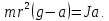 Груз на нити движется равноускоренно, проходимый им путь можно найти по формуле  Зная время движения и путь, можем найти ускорение груза. 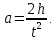 Тогда момент инерции маятника  Момент инерции крестовины 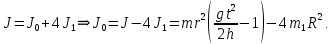 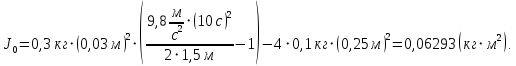 Ответ:  . .6.45. На барабан радиусом  намотан шнур, к концу которого привязан груз массой намотан шнур, к концу которого привязан груз массой 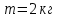 . Найти момент инерции барабана, если известно, что груз опускается с высоты . Найти момент инерции барабана, если известно, что груз опускается с высоты  за за 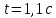 . .
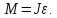 Натяжение нити создаётся весом груза 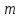 , привязанного к нити. На груз действуют: по направлению движения – сила тяжести , привязанного к нити. На груз действуют: по направлению движения – сила тяжести  , против направления движения – сила натяжения нити , против направления движения – сила натяжения нити 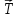 . По второму закону Ньютона для груза в проекции на вертикаль: . По второму закону Ньютона для груза в проекции на вертикаль: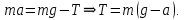 Ускорение  движения груза, равное тангенциальному ускорению движения точек на барабане, пропорционально угловому ускорению барабана. движения груза, равное тангенциальному ускорению движения точек на барабане, пропорционально угловому ускорению барабана.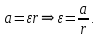 Груз на нити движется равноускоренно, проходимый им путь можно найти по формуле  Зная время движения и путь, можем найти ускорение груза. 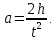 Второй закон Ньютона для вращательного движения барабана примет вид:   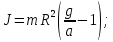  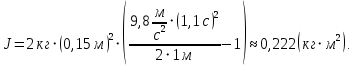 Ответ:  . .6.44. Через блок, массой которого можно пренебречь, перекинута нить, на которой висят две гири с массами 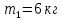 и и 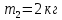 . Найти ускорение, с которым будут двигаться гири, и силу натяжения нити. . Найти ускорение, с которым будут двигаться гири, и силу натяжения нити.
  Сложим оба уравнения системы, чтобы выразить величину ускорения грузов.    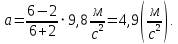 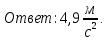 6.43. Маховик радиусом 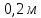 и массой и массой  соединён с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения, соединён с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения, 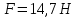 . Какую частоту вращения будет иметь маховик через . Какую частоту вращения будет иметь маховик через 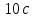 после начала вращения? Маховик считать однородным диском. Трением пренебречь. после начала вращения? Маховик считать однородным диском. Трением пренебречь.
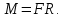 Этот момент силы сообщает маховику угловое ускорение по второму закону Ньютона. 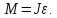 Маховик считаем однородным диском, поэтому его момент инерции 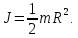 Угловое ускорение маховика  При движении с постоянным угловым ускорением угловая скорость увеличивается пропорционально времени. 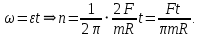 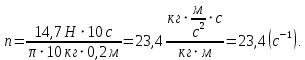 Ответ:  6.42. К ободу однородного диска радиусом 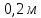 приложена касательная сила приложена касательная сила 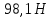 . При вращении на диск действует момент сил трения . При вращении на диск действует момент сил трения  . Найти массу диска, если известно, что диск вращается с угловым ускорением . Найти массу диска, если известно, что диск вращается с угловым ускорением  . .
Выразим массу диска из выражения второго закона Ньютона для диска. 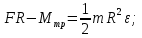  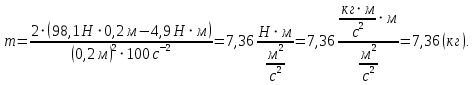 Ответ:  . .6.41. Два шара одинакового радиуса 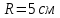 закреплены на концах невесомого стержня. Расстояние между центрами шаров закреплены на концах невесомого стержня. Расстояние между центрами шаров 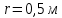 . Масса каждого шара . Масса каждого шара 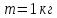 . Найти момент инерции системы относительно оси, проходящей через середину стержня перпендикулярно к нему. Какую ошибку мы допускаем, принимая шары за материальные точки? . Найти момент инерции системы относительно оси, проходящей через середину стержня перпендикулярно к нему. Какую ошибку мы допускаем, принимая шары за материальные точки?
где  – расстояние от оси вращения с известным моментом инерции тела до реального положения оси вращения. – расстояние от оси вращения с известным моментом инерции тела до реального положения оси вращения.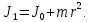 Так как инерцией соединяющего шары стержня можно пренебречь, момент инерции двух одинаковых и симметрично расположенных относительно оси вращения шаров в два раза больше момента инерции одного из них. 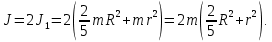  Ответ:  . .6.40. К стальному стержню, модуль упругости которого равен  , длина , длина 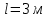 и диаметр и диаметр 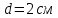 , подвешен груз массой , подвешен груз массой 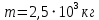 . Определить напряжение . Определить напряжение  в стержне, относительное в стержне, относительное 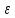 и абсолютное и абсолютное  удлинение. удлинение.
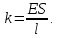 Площадь сечения стержня 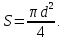 Приложенная к стержню сила равна весу груза, который в состоянии покоя груза равен силе тяжести.  Следовательно, абсолютное удлинение 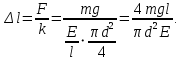   Относительное удлинение стержня  Напряжение  в стержне в стержне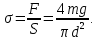  Ответ:  ; ;  ; ;  . .6.39. К проволоке диаметром 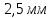 и длиной и длиной 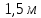 подвесили груз массой подвесили груз массой  . При этом проволока удлинилась на . При этом проволока удлинилась на 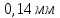 . Определить модуль упругости материала проволоки. Чему равно механическое напряжение в проволоке и её относительное удлинение? . Определить модуль упругости материала проволоки. Чему равно механическое напряжение в проволоке и её относительное удлинение?
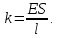 Площадь сечения стержня 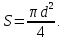 Приложенная к стержню сила равна весу груза, который в состоянии покоя груза равен силе тяжести.  Следовательно, модуль упругости материала проволоки  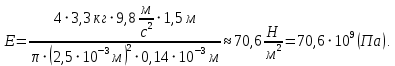 Ответ: 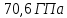 . .6.38. Плоский магнит массой 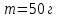 прилип к вертикально расположенной стальной плите. Для равномерного скольжения магнита вниз прикладывают силу прилип к вертикально расположенной стальной плите. Для равномерного скольжения магнита вниз прикладывают силу  . С какой силой магнит прижимается к плите? Какую силу надо приложить, чтобы равномерно перемещать магнит по плите вертикально вверх, если коэффициент трения равен . С какой силой магнит прижимается к плите? Какую силу надо приложить, чтобы равномерно перемещать магнит по плите вертикально вверх, если коэффициент трения равен 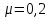 ? ?
При равномерном движении равнодействующая всех сил, действующих на магнит, равна нулю.  При движении вниз на магнит по направлению движения действует силы  и сила тяжести и сила тяжести  , а против движения сила трения , а против движения сила трения 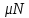 . .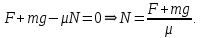  Если же магнит тянут вверх, по направлению движения действует только сила 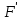 , а против движения действуют сила трения , а против движения действуют сила трения 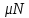 и сила тяжести и сила тяжести  . .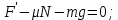 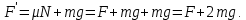 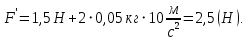 Ответ: 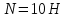 ; ; 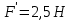 . .6.37. Самолет делает «мёртвую петлю» радиусом 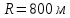 и движется по ней со скоростью и движется по ней со скоростью  . С какой силой тело пилота массой . С какой силой тело пилота массой 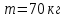 будет давить на сидение самолёта в верхней и нижней точках петли? будет давить на сидение самолёта в верхней и нижней точках петли?
Сила, с которой тело пилота давит на сидение самолёта, равно силе, с которой сидение давит на пилота, сообщая ему такое же центростремительное ускорение как у самолёта. 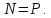 В верхней точке петли центростремительное ускорение направлено вертикально вниз, по направлению силы тяжести  , действующей на пилота. Вертикально вниз в этом случае действует и сила реакции сидения. Второй закон Ньютона в проекции на вертикаль. , действующей на пилота. Вертикально вниз в этом случае действует и сила реакции сидения. Второй закон Ньютона в проекции на вертикаль. 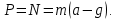 Центростремительное ускорение пропорционально квадрату скорости.  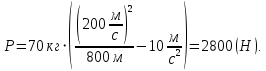 В нижней точке петли, центростремительное ускорение направление вертикально вверх. В этом случае, сила реакции сидения направлена вертикально вверх, а сила тяжести по-прежнему вертикально вниз. 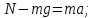  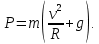  Ответ:  ; ; 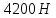 . . |


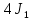 .
.



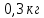
 – ?
– ?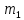 . Запишем второй закон Ньютона для каждого из грузов отдельно в проекции на направление движения.
. Запишем второй закон Ньютона для каждого из грузов отдельно в проекции на направление движения.
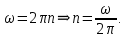
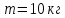
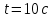
 – ?
– ?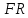 , и силы трения, действующей против движения диска, сообщают диску угловое ускорение.
, и силы трения, действующей против движения диска, сообщают диску угловое ускорение.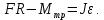
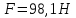

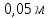
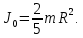
 ,
,
 материала стержня.
материала стержня.
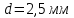
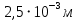


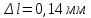

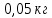
 , с такой же по величине силой плита действует на магнит горизонтально. Сила трения пропорциональна силе реакции плиты и направлена против движения.
, с такой же по величине силой плита действует на магнит горизонтально. Сила трения пропорциональна силе реакции плиты и направлена против движения.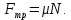

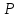 – ?
– ?