медианы. Медианы. Медиана треугольника
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Тема: «Медиана треугольника» Составители: Теоретический материал по теме «Медиана треугольника» Медиана треугольника (лат. mediāna — средняя) – это отрезок соединяющий вершины треугольника с серединой противоположной стороны. 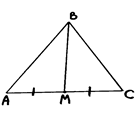 Рис.1.Отрезок ВМ – медиана треугольника АВС. Треугольник имеет три стороны, а значит и медиан у него – три.ВМ, АК, СР – медианы треугольника АВС. 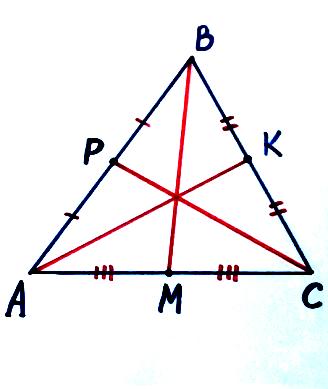 Рис. 2 Свойства медиан: 1 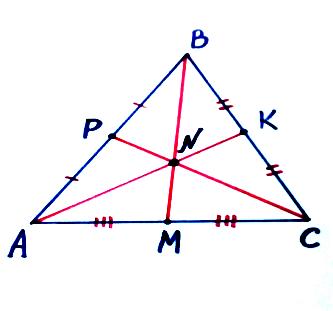 .Три медианы пересекаются в одной точкеи делятся в этой точке в отношении 2:1, считая от вершины( .Три медианы пересекаются в одной точкеи делятся в этой точке в отношении 2:1, считая от вершины(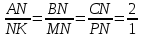 ). ).Рис 3. 2 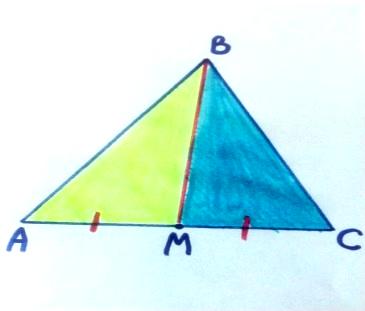 .Медиана делит треугольник на два равновеликих треугольника (SAMB=SMBC). .Медиана делит треугольник на два равновеликих треугольника (SAMB=SMBC).Рис.4 3. Все медианы делят треугольник на шесть равновеликих треугольников (SAPN=SBPN =SBKN=SCKNSCMN=SAMN). 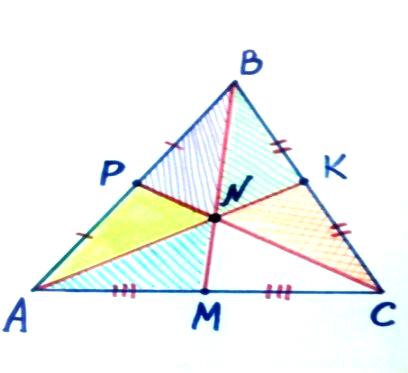 Рис. 5 4.Если точку пересечения медиан треугольника соединить отрезками с вершинами треугольника, то треугольник разделится на три равновеликих (SABN=SBCN =SACN). 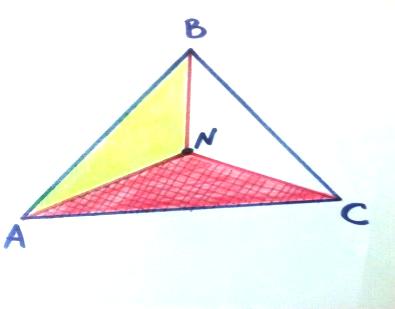 Рис.6 5.Если a, b,c – длины сторон треугольника АВС, то длины его медиан ma, mb, mcможно вычислить по формулам: 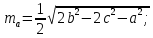 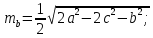 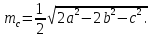 6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна половине гипотенузы и является радиусом окружности, описанной около этого треугольника (ОА=ОВ=ОС=R). Рис. 7. 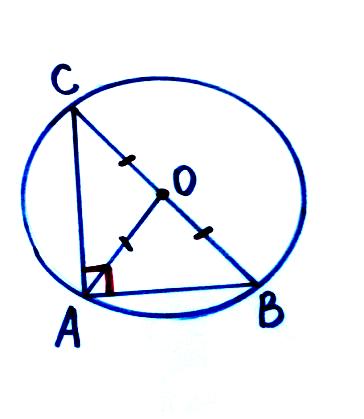 7. В равнобедренном треугольнике медиана, проведенная к основанию, является и высотой и биссектрисой (ВD - медиана, высота, биссектриса). Рис.8 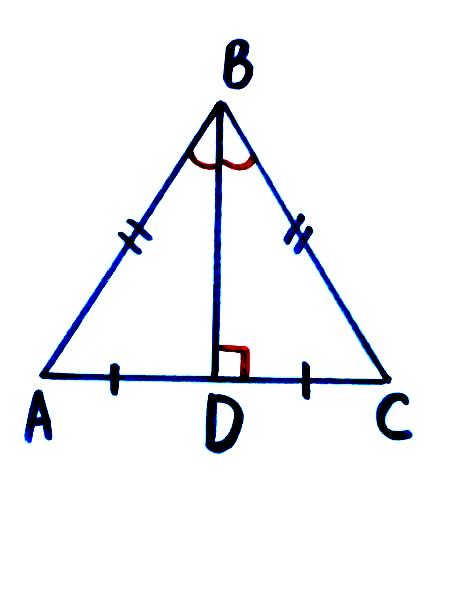 Опорные задачи Задача №1. Доказать, что медиана разбивает треугольник на два равновеликих. 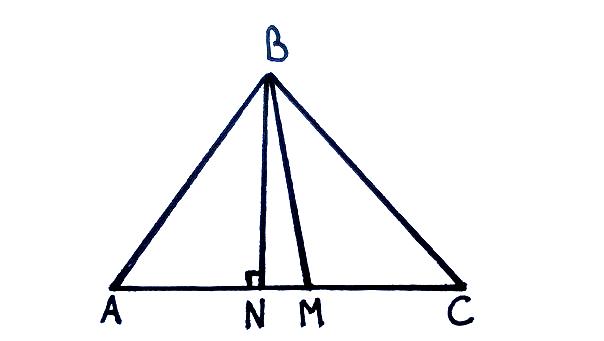 Доказательство. Рассмотрим произвольный треугольник ABC. Проведём в нём медиану BM. Треугольник разбился медианой на два треугольникаABM и CBM, имеющих равные основания AM и CM. Так как у этих треугольников общая высота BN, то SABM =½AM× BN = ½CM×BN = SCBM. Что и требовалось доказать. З 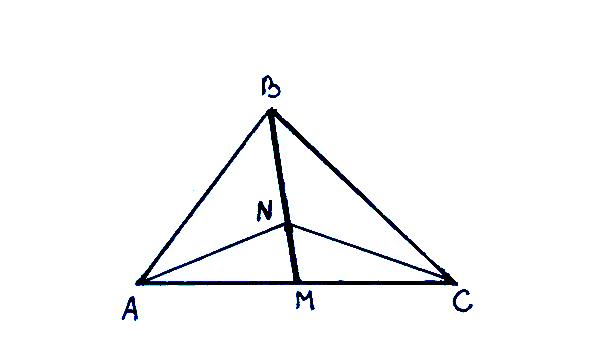 адача№ 2. Точку пересечения медиан треугольника соединили с его вершинами. Доказать, что площади образовавшихся треугольников равны. адача№ 2. Точку пересечения медиан треугольника соединили с его вершинами. Доказать, что площади образовавшихся треугольников равны.Доказательство:Пусть N - точка пересечения медиан треугольника ABC , M – середина стороны AC. Тогда MN – медиана треугольника ANC и треугольники ANM и СNM равновелики (смотри задачу №1). Поскольку BM - медиана треугольника ABC , то равновелики и треугольники ABM и CBM. Следовательно, площади треугольников ABN и СBN равны. Аналогично доказывается , что равны площади треугольников ABN и CAN . Из сказанного следует , что равны площади треугольников SABN=SBCN =SACN . Что и требовалось доказать. Задача3. Доказать что медианы треугольника, пересекаясь делят его на шесть равновеликих треугольников. Д 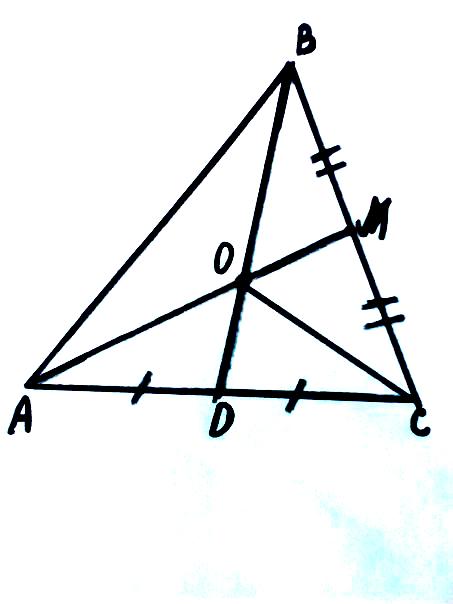 оказательство: оказательство:Для доказательства этого факта воспользуемся уже доказанными в задачах №1 и №2 фактами: SВОС = ⅓ SАВС, SОМВ= SОМС = ½ SВОС, из чего и следует, что SОМВ = SОМС = 1/6 SАВС, что и требовалось доказать. Задача 4. Доказать, что все медианы треугольника пересекаются в одной точке и делятся в этой точке в отношении 2:1. Доказательство: 1 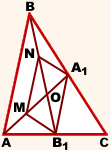 ) Пусть дан ) Пусть дан ABC, AA1, BB1, CC1 — медианы треугольника, ABC, AA1, BB1, CC1 — медианы треугольника,M — середина отрезка AO, N — середина BO (то есть AM=OM, BN=ON). 2) Соединим точки M, N, A1 и B1 отрезками. Тогда MN — средняя линия треугольника AOB и 3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC. Следовательно, A1B1 — средняя линия треугольника ABC и 4) Имеем: Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку параллелограмма). По свойству диагоналей параллелограмма Таким образом, из чего следует, что 5) Докажем теперь, что все медианы треугольника пересекаются в одной точке ( методом от противного). Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O. Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию. Таким образом, Что и требовалось доказать. З 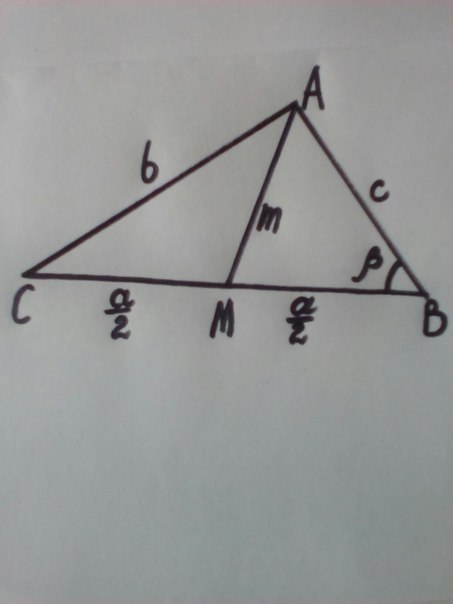 адача 5. Вывести формулу длины медианы треугольника через длины его сторон адача 5. Вывести формулу длины медианы треугольника через длины его сторон Решение. П 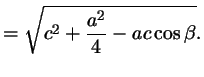 усть стороны треугольника равны усть стороны треугольника равны
С другой стороны, по теореме косинусов уже для всего треугольника 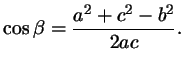 Подставляя это в предыдущую формулу, получим (после упрощений) вот что: В треугольнике со сторонами У этой задачи есть и другой, ещё более простой способ решения. Надо достроить треугольник до параллелограмма, и воспользоваться тем, что в параллелограмме сумма квадратов длин его всех сторон равна сумме квадратов его диагоналей. 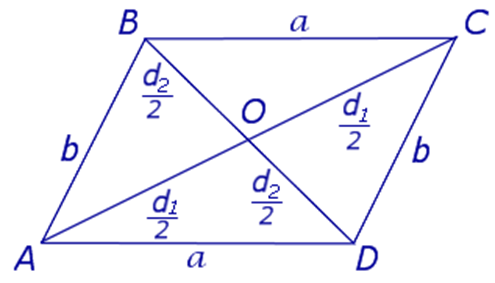 Ответ: 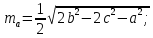 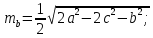 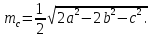 Задача 6. Доказать, что медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. Доказательство. 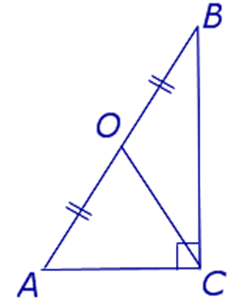 Доказательство. Продолжим медиану CO за точку O до точки D так, чтобы было выполнено равенство CO = OD, и соединим полученную точку D с точками A и B. 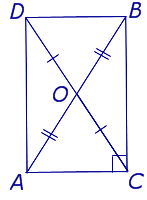 Получим четырехугольник ADBC, диагонали которого в точке пересечения делятся пополам. В силу признака параллелограмма заключаем, что четырехугольник ADBC является параллелограммом, а поскольку полученный параллелограмм содержит прямой угол C, то и все его углы прямые, следовательно, четырехугольник ADBC – прямоугольник. Поскольку диагонали прямоугольника равны, получаем равенства: что и требовалось доказать. 1) Центром окружности описанной около прямоугольного треугольника, является середина гипотенузы. 2) Радиус окружности, описанной около прямоугольного треугольника равен половине гипотенузы. Эти самые первые задачи – теоремы темы в своем решении опираются либо на предыдущие из данной темы, либо на теоремы, которые нам уже известны.На знании таких опорных задач, базируется решение многих других. Уровень 1. Вариант 1. Задача 1. Медиана равностороннего треугольника равна 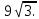 Найти сторону этого треугольника. Найти сторону этого треугольника.Ответ: 18. Задача 2. В треугольнике ABC известно, что AC=54, BM–медиана, BM=43. Найти AM. Ответ: 27. Задача 3. В треугольнике MEN известно, что EF=18, MK=15. Найти NK. 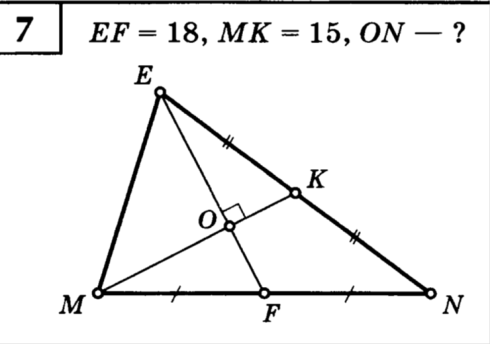 Ответ: 13. Задача 4. В треугольнике BKM известно, QM=9, BT=12. Найти площадь треугольника BOQ. 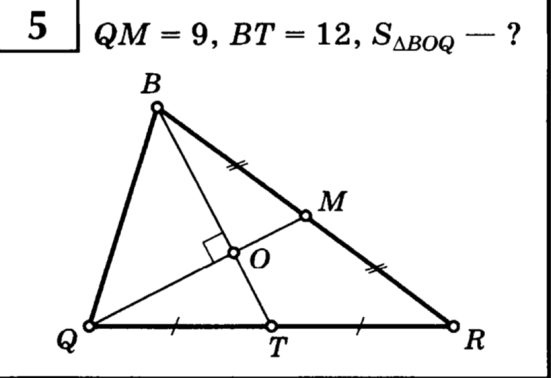 Ответ: 24. Задача 5. В треугольнике RMN известно, что RK=12, MN=20, MF=FB=RE=EN. Найти площадь треугольника MRN. 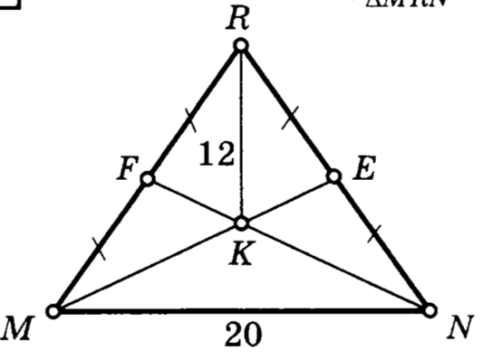 Ответ: 180. Задача 6. В треугольнике ABC известно, что AA1=12, BB1=9. Найти AB. 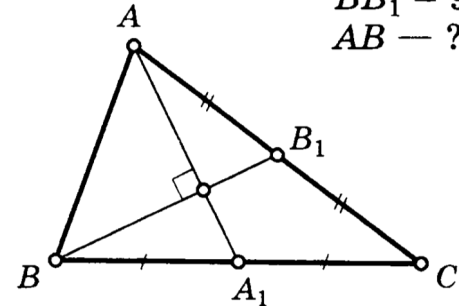 Ответ: 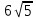 . .Вариант 2. Задача 1. Медиана равностороннего треугольника равна 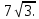 Найти сторону этого треугольника. Найти сторону этого треугольника.Ответ: 14. Задача 2. В треугольнике ABC известно, что AC=64, BM–медиана, BM=53. Найти AM. Ответ: 32. Задача 3. В треугольнике MEN известно, что EF=12, MK=9. Найти NK.  Ответ: 10. Задача 4. В треугольнике BKM известно, QM=18, BT=15. Найти площадь треугольника BOQ.  Ответ: 30. Задача 5. В треугольнике RMN известно, что RK=16, MN=20, MF=FB=RE=EN. Найти площадь треугольника MRN.  Ответ: 240. Задача 6. В треугольнике ABC известно, что AA1=12, BB1=9. Найти BC.  Ответ: 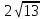 . .Уровень 2. Вариант 1. Задача 1. В треугольнике АВС АВ=4, ВС=5, АС=6. Найти длину медианы АМ. Ответ: 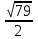 . .Задача 2. Медианы CM и BN прямоугольного треугольника АВС ( С= 900), перпендикулярны. Найти катеты, если гипотенуза равна с. Ответ: 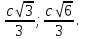 Задача 3. В прямоугольном треугольнике медианы, проведенные к катетам равны 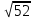 и. и.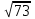 Найти длину гипотенузы. Найти длину гипотенузы.Ответ:10. Задача 4. Две стороны треугольника равны 6см и 8 см. Медианы, проведенные к этим сторонам, пересекаются под прямым углом. Найти третью сторону треугольника. Ответ: 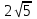 см. см.Вариант 2. Задача 1. В треугольнике АВС АВ=3, ВС=5, АС=7. Найти длину медианы АМ. Ответ: 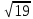 . .Задача 2.Медианы треугольника ABC пересекаются в точке M.Найдите длину медианы, проведенной к стороне BC, если угол BAC равен 470, угол BMC равен 1330, BC= 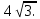 Ответ:6 Задача 3. ПрямаяAD, перпендикулярная медиане BM треугольника ABC, делит её пополам. Найдите сторону AC, если сторона ABравна 4. (Комментарий: определение медианы, свойства равнобедренного треугольника) Ответ:8. Задача 4. Две стороны треугольника равны 6см и 8 см. Медианы, проведенные к этим сторонам, пересекаются под прямым углом. Найти третью сторону треугольника. Ответ: 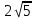 . .Задачи для самостоятельного решения 1. В равнобедренном треугольнике основание равно 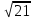 , угол при основании 30 , угол при основании 30 . Найти длину медианы, проведенной к боковой стороне. . Найти длину медианы, проведенной к боковой стороне.Ответ: 3,5. 2. Основание АС равнобедренного треугольника АВС равно 6 см, боковые стороны АВ и ВС равны 5 см. Найти расстояние между точкой пересечения медиан и точкой пересечения биссектрис треугольника. Ответ: 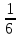 см. см.3. Медиана, проведенная к одной из боковых сторон равнобедренного треугольника, делит периметр треугольника на две части длиной 15см и 6 см. Найти длины сторон треугольника. Ответ:10 см; 10 см; 1 см. 4. В прямоугольном треугольнике медианы, проведенные к катетам равны 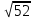 и и 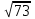 . Найти длину гипотенузы этого треугольника. . Найти длину гипотенузы этого треугольника.Ответ: 10. 5. Медиана прямоугольного треугольника, проведенная к гипотенузе, разбивает его на два треугольника с периметрами 16 и 18. Тогда длина гипотенузы равна… Ответ: 10. 6. Основание треугольника равно 26. Медианы боковых сторон равны 30 39. Площадь этого треугольника равна… Ответ:720. 7. Боковая сторона равнобедренного треугольника равна 4, медиана, проведенная к боковой стороне, равна 3. Основание этого треугольника равно… Ответ: 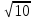 . .8. В треугольнике АВС медиана АD и биссектриса ВЕ перпендикулярны и пересекаются в точке F, известно что площадь треугольника DEF равна 5. Тогда площадь треугольника АВС равна… Ответ: 60. 9. В треугольнике АВК точки К и N – середины сторон АВ и АС соответственно. Через вершину В проведена прямая, которая пересекает сторону Ас в точке F, а отрезок КN в точке L так, что KN:LN=3:2. Определить площадь четырехугольника AKLF,если площадь треугольника АВС равна 40. Ответ: 9. 10. Стороны треугольника равны 3, 4 и 5. Определить площади треугольников, на которые разбивается данный треугольник высотой и медианой, проведенными к большей по величине стороне. Ответ: 2, 16; 3; 0,84 11. На медиане ВD треугольника АВС, площадь которого равна S, взята точка Е так, что 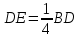 . Через точку Е проведена прямая АЕ, пересекающая сторону ВС в точке Р. Найти площадь треугольника АРС. . Через точку Е проведена прямая АЕ, пересекающая сторону ВС в точке Р. Найти площадь треугольника АРС.Ответ: 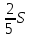 . . |
