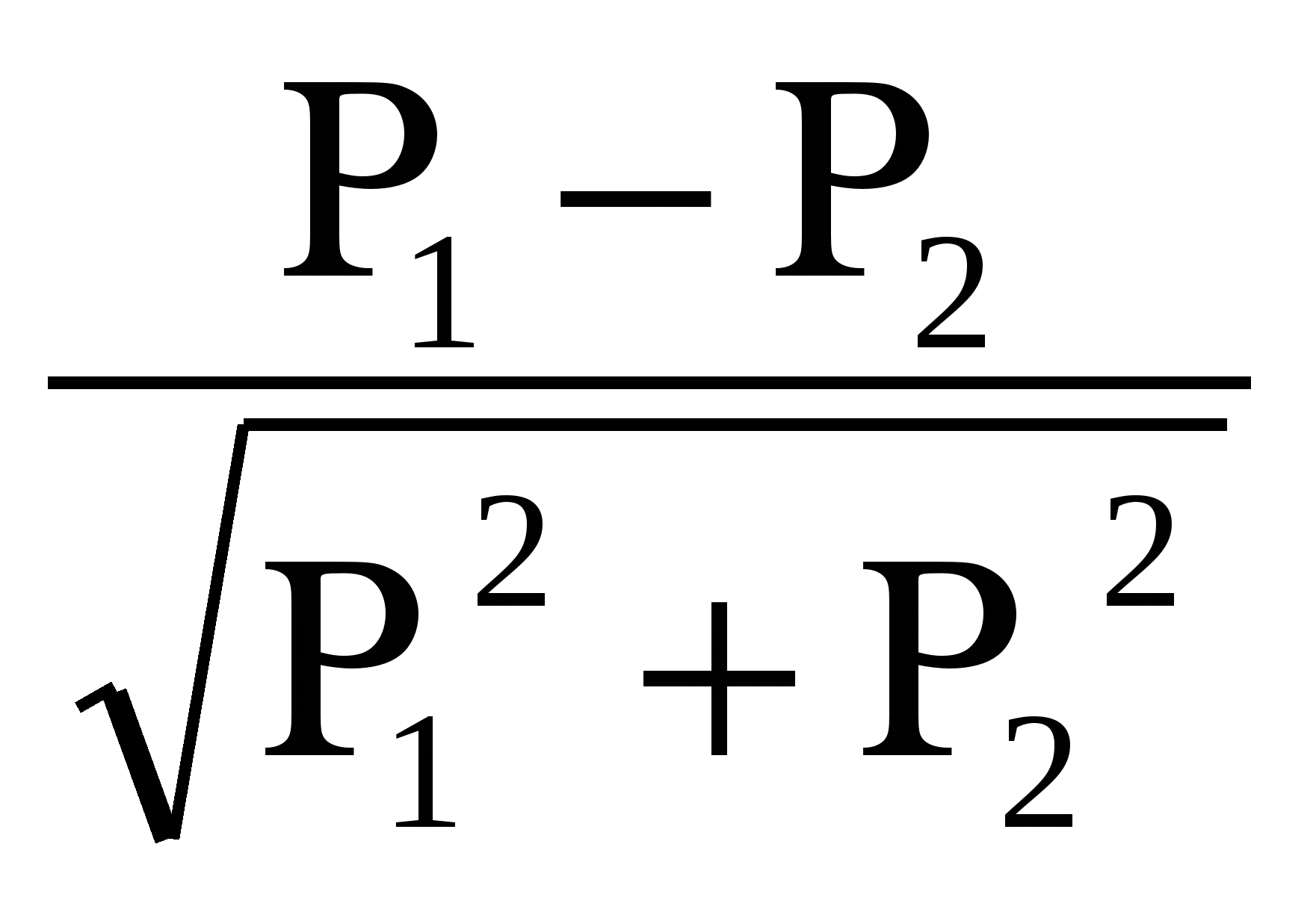Testy ОЗиЗ. Медицинская статистика
 Скачать 1.96 Mb. Скачать 1.96 Mb.
|
Методы изучения корреляционных связейДОПОЛНИТЕ: 241. Наиболее простым методом определения силы связи между признаками является метод ________ корреляции. 242. Наиболее точным методом определения силы связи между признаками является метод ________. 243. Корреляционная связь может быть прямой и ________. 244. Коэффициент корреляции, равный нулю, свидетельствует об ________ связи между явлениями. 245. Коэффициент корреляции, равный единице, свидетельствует о ________ связи между явлениями. 246. Коэффициент ранговой корреляции рассчитывается при числе коррелируемых пар не менее ________. 247. Связь между признаками считается статистически значимой, если величина коэффициента корреляции больше или равна табличной величине при р = ________. 248. Связь между признаками считается статистически значимой, если коэффициент корреляции превышает свою ошибку в ________ раза и более 249. Коэффициент регрессии показывает изменение величины одного признака при изменении величины второго на ________. ВЫБЕРИТЕ ПРАВИЛЬНЫЙ ОТВЕТ: 250. Корреляционная связь характеризуется соответствием 1) одного значения факторного признака нескольким значениям результативного признака 2) нескольких значений факторного признака нескольким значениям результативного признака 3) одного значения факторного признака строго определенному значению результативного признака 251. Практическое использование корреляционного анализа 1) расчет обобщающих коэффициентов, характеризующих различные стороны каждого из изучаемых признаков 2) сравнение степени однородности исследуемых совокупностей 3) определение пределов возможных колебаний совокупностей 4) выявление взаимодействия факторов, определение силы и направления влияния одних факторов на другие 252. Корреляционный анализ используется для 1) расчета обобщающих коэффициентов, характеризующих различные стороны каждого из изучаемых признаков 2) сравнения степени однородности исследуемых совокупностей 3) установления пределов возможных колебаний выборочных показателей при данном числе наблюдений 4) выявления взаимодействия факторов, определения силы и направленности связи 253. Корреляционной называется связь 1) характеризующая совокупность по ее гомогенности и распределение двух сравниваемых признаков 2) при которой значению каждой величины одного признака соответствует несколько значений другого взаимосвязанного с ним признака 3) при которой любому значению одного из признаков соответствует строго определенное значение другого взаимосвязанного с ним признака 254. Функциональной называется связь 1) при которой каждому значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака 2) характеризующая совокупность по ее гомогенности и распределение двух сравниваемых признаков 3) при которой любому значению одного из признаков соответствует строго определенное значение другого взаимосвязанного с ним признака 255. Расчет коэффициента ранговой корреляции используется для 1) определения взаимосвязи между двумя меняющимися признаками 2) установления взаимосвязи между двумя количественными признаками, один из которых выражен в виде интервалов значений 3) оценки достоверности различия двух величин 256. Формула для расчета коэффициента ранговой корреляции 1) 2) 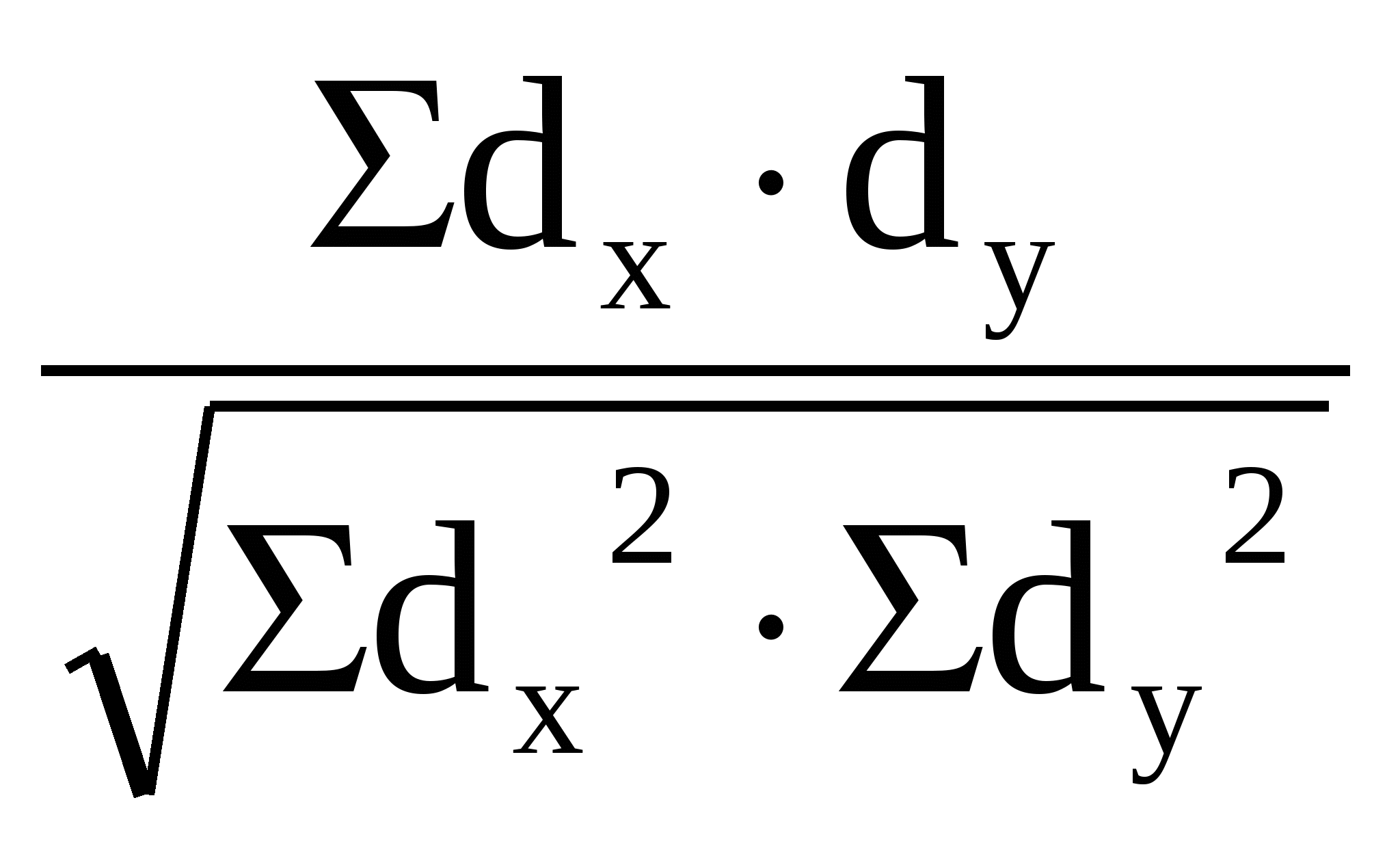 4) 4) 257. Расчет ρху используется для 1) определения достоверности различия между несколькими совокупностями по распределению в них какого-либо признака 2) оценки достоверности различия двух средних величин 3) определения взаимосвязи между двумя количественными признаками, один из которых представлен в виде интервалов значений 258. Формула для расчета коэффициента линейной корреляции (Пирсона) 1) 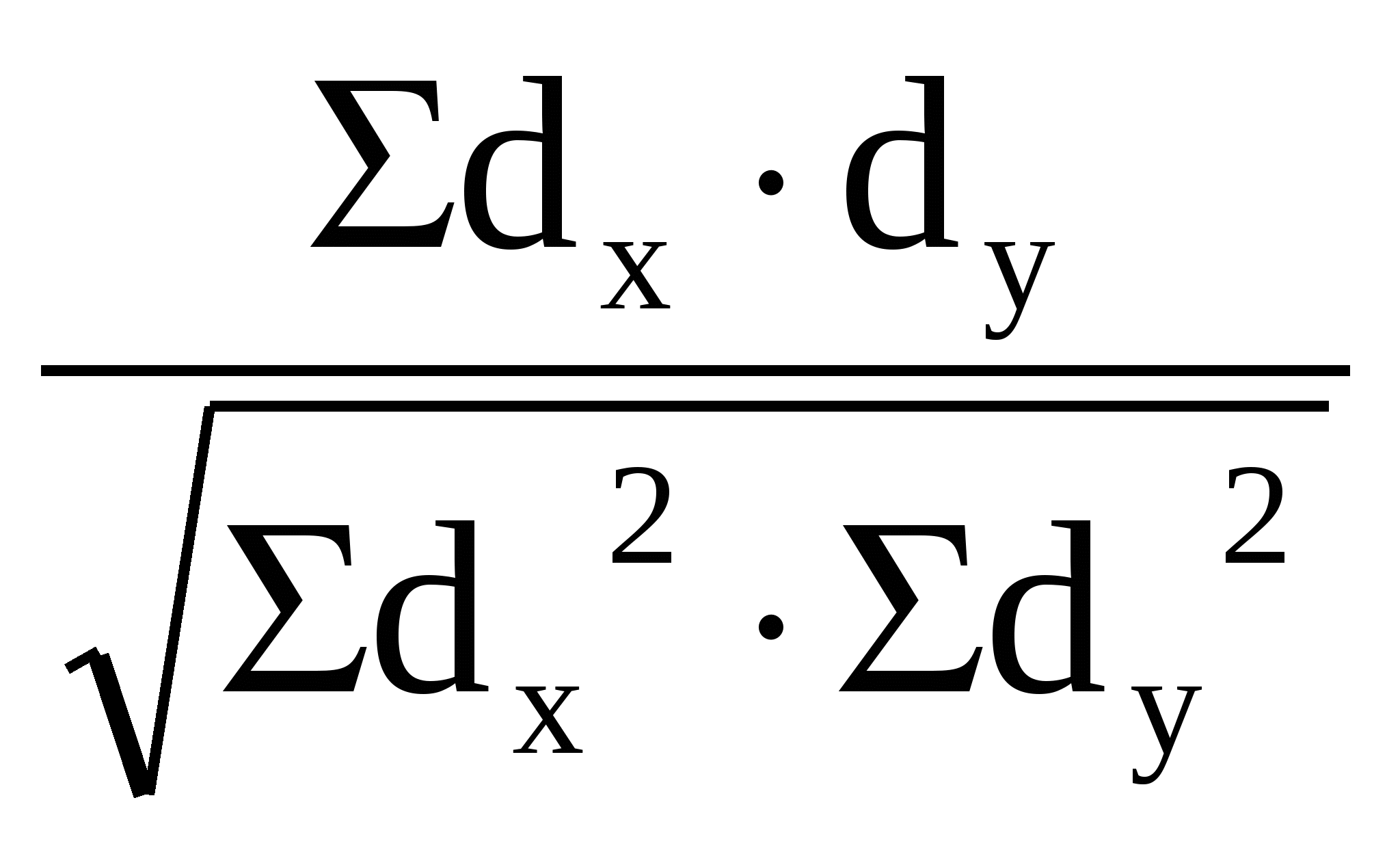 3) 3) 259. Значение коэффициента корреляции, превышающее табличное значение при р = 95%, подтверждает статистическую 1) достоверность взаимосвязи 2) достоверность различия 3) недостоверность взаимосвязи 4) недостоверность различия 260. Коэффициент регрессии на практике применяется для расчета 1) ориентировочных данных об уровне силы связи 2) точных данных об уровне силы связи 3) силы связи между количественными признаками. 4) изменения величины одного признака при изменении величины другого признака на единицу 261. Укажите минимальное число наблюдений при малой выборке 1) 20 наблюдений 2) 30 наблюдений 3) 50 наблюдений 4) 100 наблюдений 5) при использовании различных статистических методов максимальное число наблюдений варьирует 262. В каких пределах может колебаться значение коэффициента корреляции? 1) от 0 до 1 4) от –1 до +1 2) от 0 до 2 5) от –10% до +10% 3) от 0,5 до 1 УСТАНОВИТЕ СООТВЕТСТВИЕ
УСТАНОВИТЕ ПОСЛЕДОВАТЕЛЬНОСТЬ: 274. Расчет коэффициента корреляции по методу Пирсона: 1) расчет квадратов отклонений dх2 и dу2 и суммирование их произведений 2) оценка достоверности значения rху по специальной таблице 3) расчет средней арифметической для ряда х и ряда у 4) суммирование произведений dх и dу 5) нахождение отклонений dх и dу от средней арифметической этих рядов 6) расчет коэффициента по формуле | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||