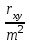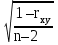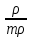озз. ОЗИЗ - тест. Медицинская статистика
 Скачать 364.51 Kb. Скачать 364.51 Kb.
|
Оценка достоверности результатов исследованияДОПОЛНИТЕ 180. Достоверность результатов исследования зависит от РЕПРЕЗЕНТАТИВНОСТИ статистической совокупности. 181. Свойство репрезентативности присуще ВЫБОРОЧНОЙ совокупности. 182. При вероятности безошибочного прогноза, равной 95%, коэффициент Стьюдента (t) равен 2. 183. Критический уровень вероятности безошибочного прогноза в медицинских исследованиях равен 95% 184. Доверительный интервал тем больше, чем больше ___средняя ошибка(m) при неизменной величине критерия Стьюдента. 185. Доверительные границы – это границы, в пределах которых будет находиться средняя или относительная величина в ГЕНЕРАЛЬНОЙ совокупности. 186. С увеличением числа наблюдений средняя ошибка средней арифметической величины УМЕНЬШАЕТСЯ. 187. Разность между результатами двух исследований, выраженных средними или относительными величинами, достоверна при t = 2. 188. При критическом уровне вероятности безошибочного прогноза (95%) коэффициент Стьюдента равен 2. 189. Ошибка расчетной статистической величины выборочной совокупности уменьшается при УВЕЛИЧЕНИИ числа наблюдений. 190. Уменьшение числа наблюдений в выборочной совокупности приводит к УВЕЛИЧЕНИЮ ошибки средней арифметической. ВЫБЕРИТЕ ПРАВИЛЬНЫЙ ОТВЕТ: 191. При вероятности безошибочного прогноза Р = 87% результаты медико-биологических исследований 1) достоверны 2) не достоверны 3) относительно достоверны 192. К критериям оценки достоверности относятся 1) лимит и ошибка репрезентативности 2) ошибка репрезентативности и доверительные границы 3) доверительные границы и коэффициент вариации 193. Критерий Стьюдента, равный 3.4, свидетельствует о статистической 1) достоверности различия двух статистических величин 2) недостоверности различия двух относительных величин 3) недостоверности различия двух средних величин ?194. Критерий Стьюдента, равный 1,5, свидетельствует о 1) достоверности результатов исследования ?2) недостоверности результатов исследования 3) относительной достоверности результатов исследования 195. При вероятности безошибочного прогноза Р = 97% медико-биологические исследования статистически 1) достоверны 2) относительно достоверны 3) не достоверны 196. При вероятности безошибочного прогноза Р = 95% результаты медико-биологических исследований статистически 1) достоверны 2) не достоверны 3) ошибочны ?197. При вероятности ошибки р = 3% результаты медико-биологических исследований 1) достоверны ?2) не достоверны 3) относительно достоверны 198. При вероятности ошибки р = 6% результаты медико-биологических исследований 1) достоверны 2) не достоверны 3) относительно достоверны 199. Формула m = ± 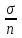 используется для расчета используется для расчета1) доверительных границ 2) ошибки репрезентативности относительной величины 3) ошибки репрезентативности средней величины 4) среднего квадратического отклонения 200. Формула М ± tm используется для определения 1) средней квадратической величины 2) оценки достоверности различий 3) коэффициента корреляции 4) доверительного интервала 201. Критерий Стьюдента используется для 1) определения взаимосвязи между двумя меняющимися признаками 2) оценки достоверности различия двух относительных величин 3) сравнения двух и более относительных величин, полученных на неоднородных совокупностях 4) оценки достоверности различия двух и более относительных величин ?202. Разница между двумя относительными показателями считается достоверной, если превышает свою ошибку 1) в 2 и более раза 2) менее чем в 2 раза 3) в 3 и более раза 203. В каких границах возможны случайные колебания средней величины с вероятностью 95,5% 1) M±m 2) M±2m 3) M±3m 204. Какой степени вероятности соответствует доверительный интервал Р±2m 1) вероятности 68,3% 3) вероятности 97,7% 2) вероятности 95,5% 205. Какой степени вероятности соответствует доверительный интервал М±3m 1) вероятности 68,3% 2) вероятности 95,5% 3) вероятности 97,7% 206. Разница между средними величинами считается достоверной, если 1) t = 1 2) t = 2 и больше 3) t = 3 и больше 207. Минимальное значение вероятности в медицинских исследованиях должно составлять 1) 68,3% 2) 74,6% 3) 95,5% 208. Формула для расчета достоверности различий средних величин по t-критерию 1) 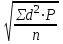 4) А + 4) А + 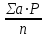 2) 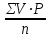 5) 5) 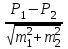 +3) 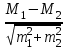 УСТАНОВИТЕ СООТВЕТСТВИЕ:
Коэффициент согласия 2ДОПОЛНИТЕ: 210. Для определения достоверности различия между явлениями при сравнении двух групп и более используется критерий х2. 211. Используемые для вычисления χ2 частоты должны быть выражены в АБСОЛЮТНЫХ величинах. 212. При вычислении χ2 в группе должно быть не менее 5 наблюдений. 213. Коэффициент критерия χ2 разработал ПИРСОН. 214. Достоверность полученного значения χ2 оценивают по таблице. 215. Существуют 2 метода расчета критерия χ2. 216. Упрощенный способ расчета χ2 используется только при числе степеней свободы, равном 1. 217. Различие признаков считается достоверным, если χ2 больше или равен табличному значению с вероятностью ошибки 0,05. 218. Если ожидаемые и фактические данные равны, то χ2 равен 0. ВЫБЕРИТЕ ПРАВИЛЬНЫЙ ОТВЕТ: 219. Критерий согласия является критерием 1) параметрическим 2) непараметрическим 220. «Нулевая» и «рабочая» гипотезы при определении χ2 1) идентичны 2) альтернативны 3) дополняют друг друга 221. Достоверность различия между сравниваемыми совокупностями тем больше, чем величина χ2 1) больше 2) меньше 222. При числе степеней свободы, равном 1 для расчета критерия согласия применяется 1) 1 способ 2) 2 способа 3) 3 способа 223. При числе степеней свободы, равном 3 для расчета критерия согласия используется 1) 1 способ 3) 3 способа 2) 2 способа 4) 4 способа 224. Критерий χ2 применяется для оценки 1) достоверности доверительных границ признака 2) разнообразия признаков вариационных рядов 3) достоверности различия между двумя совокупностями и более 4) однородности исследуемых совокупностей 225. Критерий χ2 используется для 1) сравнения двух и более относительных величин, полученных на неоднородных совокупностях 2) оценки достоверности различия двух средних величин 3) определения взаимосвязи между двумя меняющимися количественными признаками 4) определения достоверности различия между несколькими совокупностями по распределению в них атрибутивного признака 226. Критерий χ2 применяется для оценки 1) колеблемости вариационных рядов 2) достоверности взаимосвязи между двумя совокупностями и более 3) достоверности доверительных границ признака 4) пределов возможных колебаний выборочных показателей 227. В основе расчета критерия χ2 лежит 1) числовое соотношение одноименных относительных показателей структуры, рассчитанных на двух разных совокупностях 2) определение объема наблюдений для получения достоверных статистических показателей 3) установление соответствия или несоответствия между фактическими и ожидаемыми частотами распределения сравниваемых признаков 228. Формула 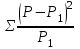 используется для определения используется для определения1) достоверности двух средних величин 2) корреляции 3) достоверности двух относительных величин 4) вариабельности признака 5) достоверности различия нескольких сравниваемых совокупностей 229. Формула для расчета критерия согласия χ2 1) 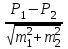 3) rxy 3) rxy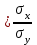 5) A + 5) A +  2)  +4) +4)  230. Показатель соответствия вычисляется по формуле +1)  3) 3)  2)  4) 4)  231. Критерий χ2 используется для 1) сравнения двух и более относительных величин, полученных на неоднородных совокупностях 2) определения взаимосвязи между двумя меняющимися количественными признаками 3) определения достоверности различия нескольких совокупностей по распределению в них атрибутивного признака 4) оценки достоверности различия двух средних величин 232. При оценке достоверности с помощью χ2 учитывается число 1) изучаемых групп 3) степеней свободы 2) пар сравниваемых признаков 4) наблюдений 233. Значение χ2 меньше, чем табличное значение при р = 0,05, подтверждает статистическую 1) недостоверность 2) достоверность результата 3) достоверность различия 234. Число степеней свободы определяется по формуле 1) K = (s – 1) (r – 1) 3) K = (s – 1) (r +1) 2) K = (s – 1) : (r – 1) 4) K = (s + 1) : ( r – 1) 235. На основании нижеприведенных данных требуется оценить зависимость между патогенностью микроорганизмов и их устойчивостью к сульфаниламидным препаратам
Укажите, какой из нижеприведенных коэффициентов позволит ответить на поставленный вопрос? 1) коэффициенты стандартизации 2) критерий соответствия 3) критерий Фишера 236. На основании нижеприведенных данных требуется определить влияние вакцинации на заболеваемость туберкулезом
Укажите, какой из нижеприведенных данных методов позволит ответить на поставленный вопрос 1) обратный метод стандартизации 3) корреляционный анализ 2) расчет критерия соответствия УСТАНОВИТЕ СООТВЕТСТВИЕ:
УСТАНОВИТЕ ПОСЛЕДОВАТЕЛЬНОСТЬ: 240. Этапы расчета критерия χ2. 2-1-4-5-3-6 1) определение ожидаемых чисел (Р1) 2) распределение фактических данных (Р) по всем группам, суммирование итогов и расчет общих показателей 3) деление квадрата разности на ожидаемое число 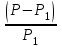 2 24) определение разностей (Р – Р1) по всем группам 5) определение квадрата разностей (Р – Р1)2 6) суммирование предыдущих результатов вычислений по всем группам Методы изучения корреляционных связейДОПОЛНИТЕ: 241. Наиболее простым методом определения силы связи между признаками является метод РАНГОВОЙ корреляции. 242. Наиболее точным методом определения силы связи между признаками является метод Пирсона. 243. Корреляционная связь может быть прямой и ОБРАТНОЙ. 244. Коэффициент корреляции, равный нулю, свидетельствует об ОТСУТСТВИИ связи между явлениями. 245. Коэффициент корреляции, равный единице, свидетельствует о ФУНКЦИОНАЛЬНОЙ связи между явлениями. 246. Коэффициент ранговой корреляции рассчитывается при числе коррелируемых пар не менее 5. 247. Связь между признаками считается статистически значимой, если величина коэффициента корреляции больше или равна табличной величине при р = 0,05. 248. Связь между признаками считается статистически значимой, если коэффициент корреляции превышает свою ошибку в 3 раза и более 249. Коэффициент регрессии показывает изменение величины одного признака при изменении величины второго на 1. ВЫБЕРИТЕ ПРАВИЛЬНЫЙ ОТВЕТ: 250. Корреляционная связь характеризуется соответствием 1)одного значения факторного признака нескольким значениям результативного признака 2) нескольких значений факторного признака нескольким значениям результативного признака 3) одного значения факторного признака строго определенному значению результативного признака 251. Практическое использование корреляционного анализа 1) расчет обобщающих коэффициентов, характеризующих различные стороны каждого из изучаемых признаков 2) сравнение степени однородности исследуемых совокупностей 3) определение пределов возможных колебаний совокупностей 4) выявление взаимодействия факторов, определение силы и направления влияния одних факторов на другие 252. Корреляционный анализ используется для 1) расчета обобщающих коэффициентов, характеризующих различные стороны каждого из изучаемых признаков 2) сравнения степени однородности исследуемых совокупностей 3) установления пределов возможных колебаний выборочных показателей при данном числе наблюдений 4) выявления взаимодействия факторов, определения силы и направленности связи 253. Корреляционной называется связь 1) характеризующая совокупность по ее гомогенности и распределение двух сравниваемых признаков 2) при которой значению каждой величины одного признака соответствует несколько значений другого взаимосвязанного с ним признака 3) при которой любому значению одного из признаков соответствует строго определенное значение другого взаимосвязанного с ним признака 254. Функциональной называется связь 1) при которой каждому значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака 2) характеризующая совокупность по ее гомогенности и распределение двух сравниваемых признаков 3) при которой любому значению одного из признаков соответствует строго определенное значение другого взаимосвязанного с ним признака 255. Расчет коэффициента ранговой корреляции используется для 1) определения взаимосвязи между двумя меняющимися признаками 2) установления взаимосвязи между двумя количественными признаками, один из которых выражен в виде интервалов значений 3) оценки достоверности различия двух величин 256. Формула для расчета коэффициента ранговой корреляции +1)  3) 3)  2)  4) 4)  257. Расчет ρху используется для 1) определения достоверности различия между несколькими совокупностями по распределению в них какого-либо признака 2) оценки достоверности различия двух средних величин 3) определения взаимосвязи между двумя количественными признаками, один из которых представлен в виде интервалов значений 258. Формула для расчета коэффициента линейной корреляции (Пирсона) 1) 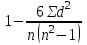 +2) +2) 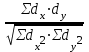 3) 3) 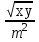 259. Значение коэффициента корреляции, превышающее табличное значение при р = 95%, подтверждает статистическую 1) достоверность взаимосвязи 2) достоверность различия 3) недостоверность взаимосвязи 4) недостоверность различия 260. Коэффициент регрессии на практике применяется для расчета 1) ориентировочных данных об уровне силы связи 2) точных данных об уровне силы связи 3) силы связи между количественными признаками. 4) изменения величины одного признака при изменении величины другого признака на единицу 261. Укажите минимальное число наблюдений при малой выборке 1) 20 наблюдений 2) 30 наблюдений 3) 50 наблюдений 4) 100 наблюдений 5) при использовании различных статистических методов максимальное число наблюдений варьирует 262. В каких пределах может колебаться значение коэффициента корреляции? 1) от 0 до 1 4) от –1 до +1 2) от 0 до 2 5) от –10% до +10% 3) от 0,5 до 1 УСТАНОВИТЕ СООТВЕТСТВИЕ
УСТАНОВИТЕ ПОСЛЕДОВАТЕЛЬНОСТЬ: 274. Расчет коэффициента корреляции по методу Пирсона:3-5-4-1-6-2 1) расчет квадратов отклонений dх2 и dу2 и суммирование их произведений 2) оценка достоверности значения rху по специальной таблице 3) расчет средней арифметической для ряда х и ряда у 4) суммирование произведений dх и dу 5) нахождение отклонений dх и dу от средней арифметической этих рядов 6) расчет коэффициента по формуле Использование методов стандартизации в | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 298. | КОЭЭФИЦИЕНТЫ: | ПРИМЕНЕНИЕ: | |
| | 1) стандартизованные в 2) корреляции б 3) наглядности е | А. Определение достоверности различия сравниваемых показателей | |
| | | Б. Определение характера и силы связи между явлениями | |
| | | В. Сравнение интенсивных показателей, полученных на неоднородных по возрасту совокупностях | |
| | | Г. Определение достоверности средних величин | |
| | | Д. Вычисление достоверности различия показателей | |
| | Ответ: 1 – __; 2 – __; 3 __. | Е. Оценка динамики смертности за 10 лет | |
УСТАНОВИТЕ ПОСЛЕДОВАТЕЛЬНОСТЬ:2-3-1-4
299. Вычисление стандартизованных показателей (прямой метод):
1) расчет условных показателей в каждой группе стандарта
2) расчет интенсивных показателей в сравниваемых группах
3) выбор стандарта
4) расчет общих стандартизованных показателей

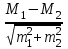
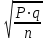
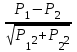
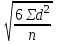
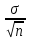
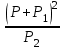 Г.
Г.