Физика - Колебания и волны. Механические колебания и волны
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
II семестр Механические колебания и волны Общая черта колебательных процессов – высокая степень повторяемости процесса. Колебания подразделяются:
Механические колебания Колебательные системы Колебания – физические процессы, которые происходят с определённой повторяемостью во времени. Периодические колебания – колебания, при которых значения характерных параметров системы повторяются через равные промежутки времени. Полное колебание – процесс, проходящие в системе за период. Период – минимальный период времени, через который все параметры системы повторяются. Частота – число полных колебаний, происходящих в единицу времени. Циклическая частота – число полных колебаний за Гармонические колебания – колебания, происходящие по закону изменения гармонических функций. Линейные колебания – колебания, возникающие в линейных системах. Линейная система – система, реакция которой линейно зависит от воздействия. Свободные (собственные) колебания – колебания, которые происходят в отсутствие внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы из состояния её устойчивого равновесия под действием внутренних сил системы. Вынужденные колебания – колебания, возникающие в какой-либо системе под влиянием переменного внешнего воздействия. Равновесие в механических системах и возникновение колебаний Условие равновесия точечного тела: Характерным свойством колебательной системы является наличие возвращающей (квазиупругой) силы. Свободные незатухающие колебания у Пружинный маятник: Математический маятник: Физический маятник: Приведённая длина физического маятника – длина математического маятника, период колебаний которого равен периоду колебаний физического маятника, Центр качания – математическая точка, отстоящая от точки подвеса на приведённую длину и лежащая на маятнике. Если физический и математический маятники с приведённой длиной колеблются около одной оси, то материальная точка математического и центр качания физического маятника движутся синхронно, если вначале их отклонили на одинаковый угол и одновременно отпустили. Точка подвеса и центр качания обратимы (можно подвесить за любую из них, период колебаний будет одинаков). Уравнение колебаний Все системы описываются уравнением Переменная колебаний – параметр, характеризующий отклонение системы от положения равновесия. (x). Решение уравнения колебаний. Линейный гармонический осциллятор – любая колебательная система, в которой возникают малые линейные гармонические колебания. Основные характеристики гармонических колебаний Амплитуда – максимальное значение переменной колебания (максимальное отклонение системы от положения равновесия). Амплитуда всегда положительна. Фаза – параметр, характеризующий относительное значения отклонения системы от положения равновесия ( Начальная фаза – значение фазы в начальный момент времени ( Период: Свойства гармонических колебаний:
Скорость и ускорение при колебаниях: Пусть Начальные условие – задание смещение и скорости в начальный момент времени.
Задание начальных условий определяет амплитуду и начальную фазу. Кинетическая и потенциальная энергия системы: Э 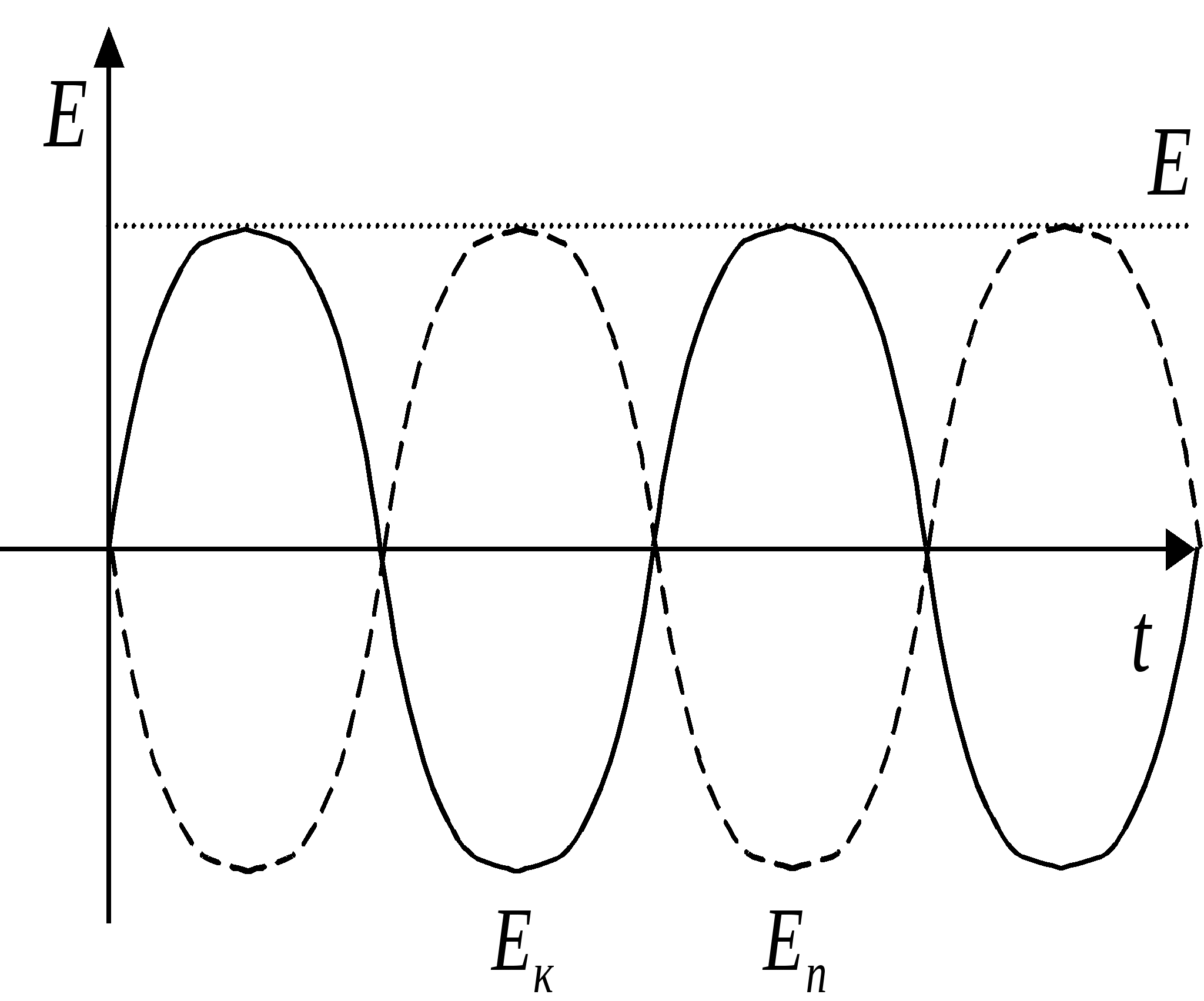 нергия и вычисление периода колебаний: нергия и вычисление периода колебаний:
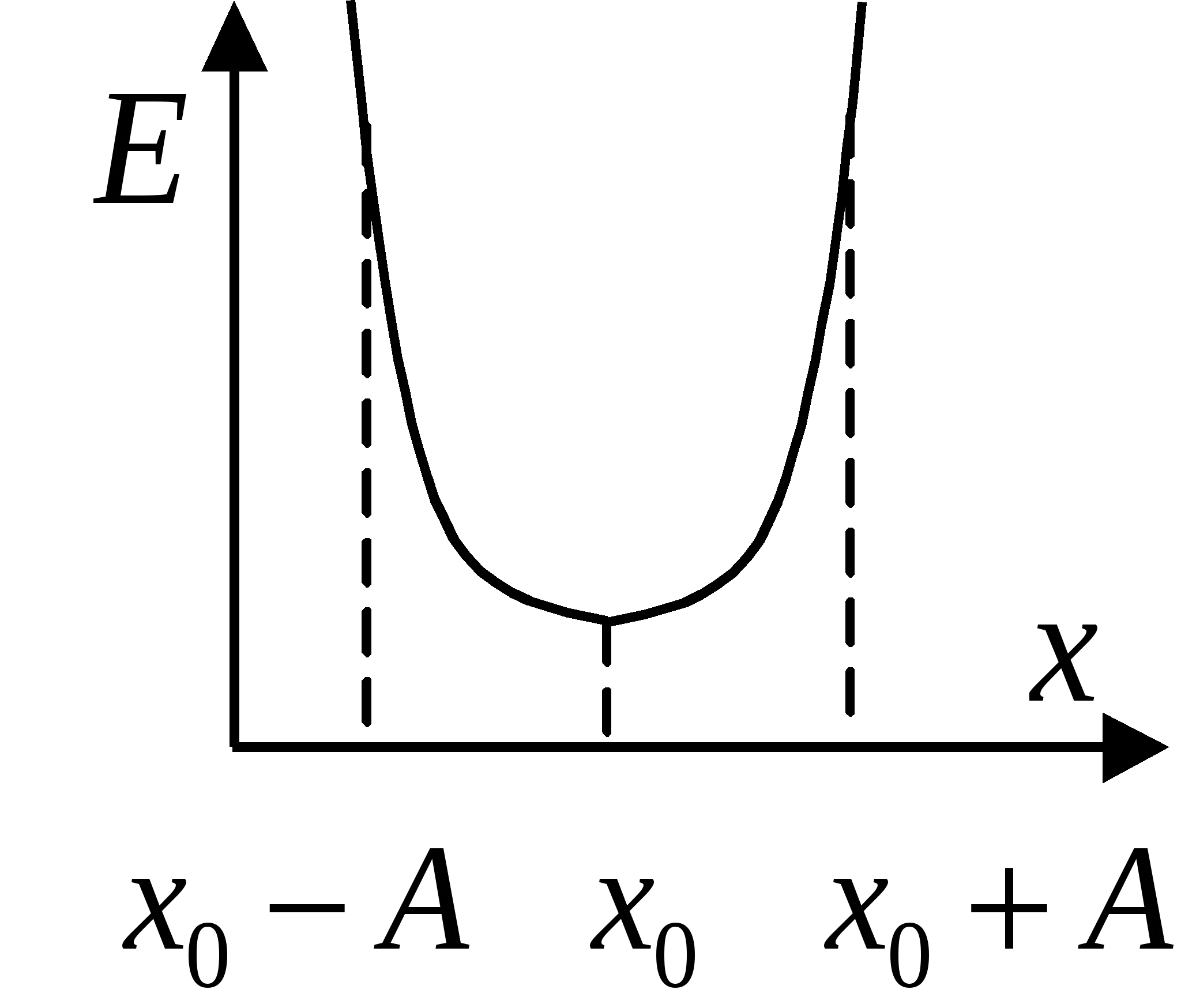
Представление колебаний с помощью векторных диаграмм и комплексных чисел. П 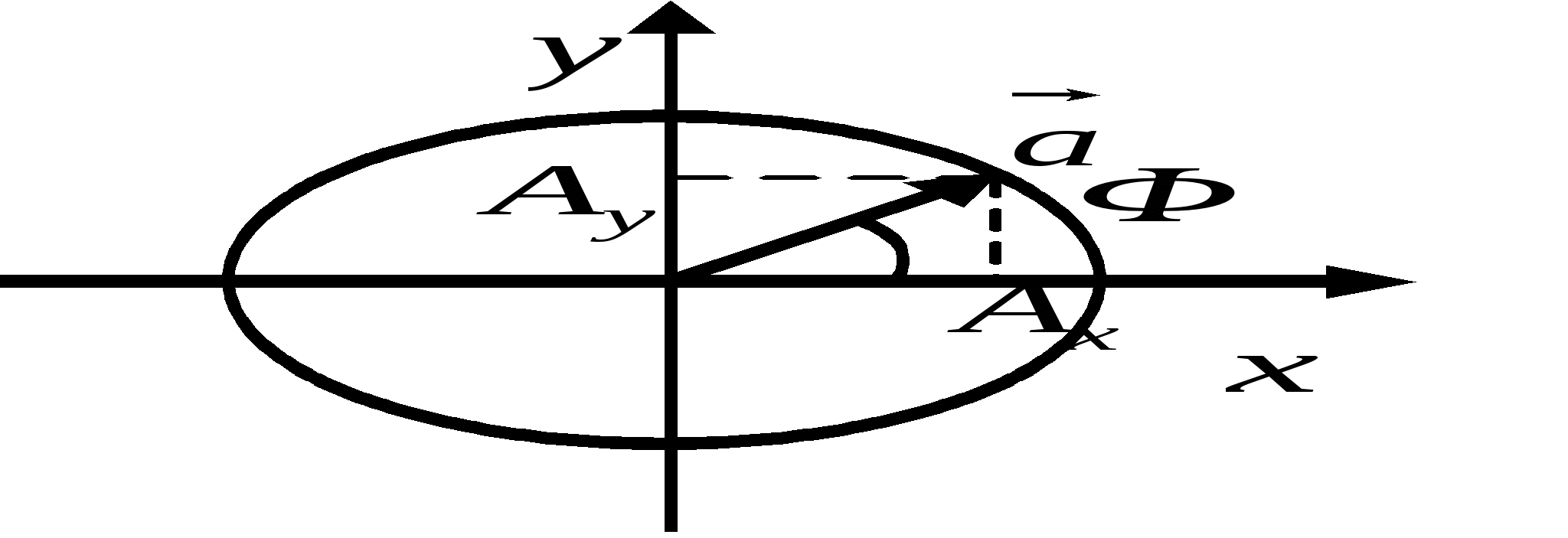 усть усть Фазовая плоскость (пространство) – геометрический образ, представимый множеством состояний системы Фазовая точка – точка фазовой плоскости, определяемая скоростью и координатой и соответствующая определённому состоянию системы. Фазовая траектория – линия, которую описывает точка на фазовой плоскости при изменении состояния системы. Фазовый портрет маятника – фазовая траектория маятника: Ф 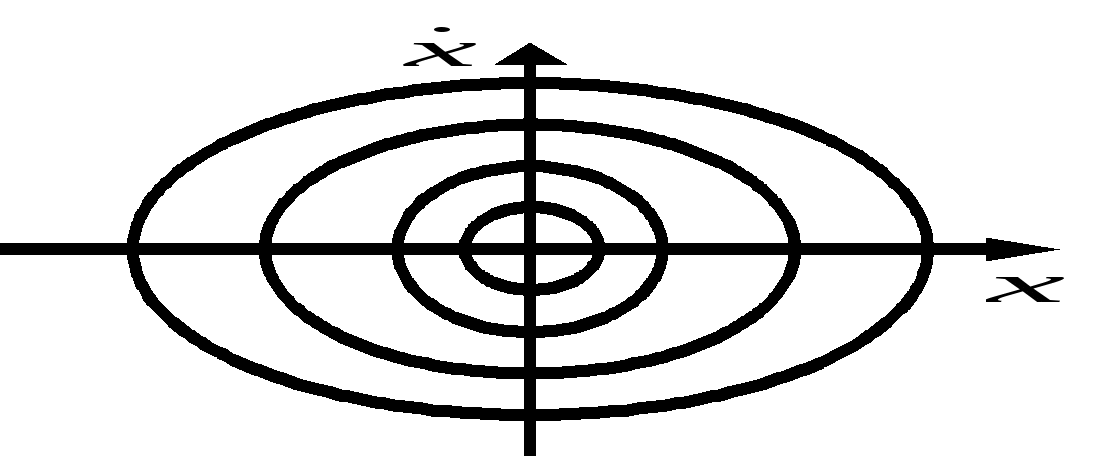 азовый портрет для гармонических колебаний: азовый портрет для гармонических колебаний: Свободные затухающие колебания Пружинный маятник: Математический маятник: Решение уравнения свободных затухающих колебаний: Предположим, что Если трение мало Основные характеристики затухающих колебаний. В 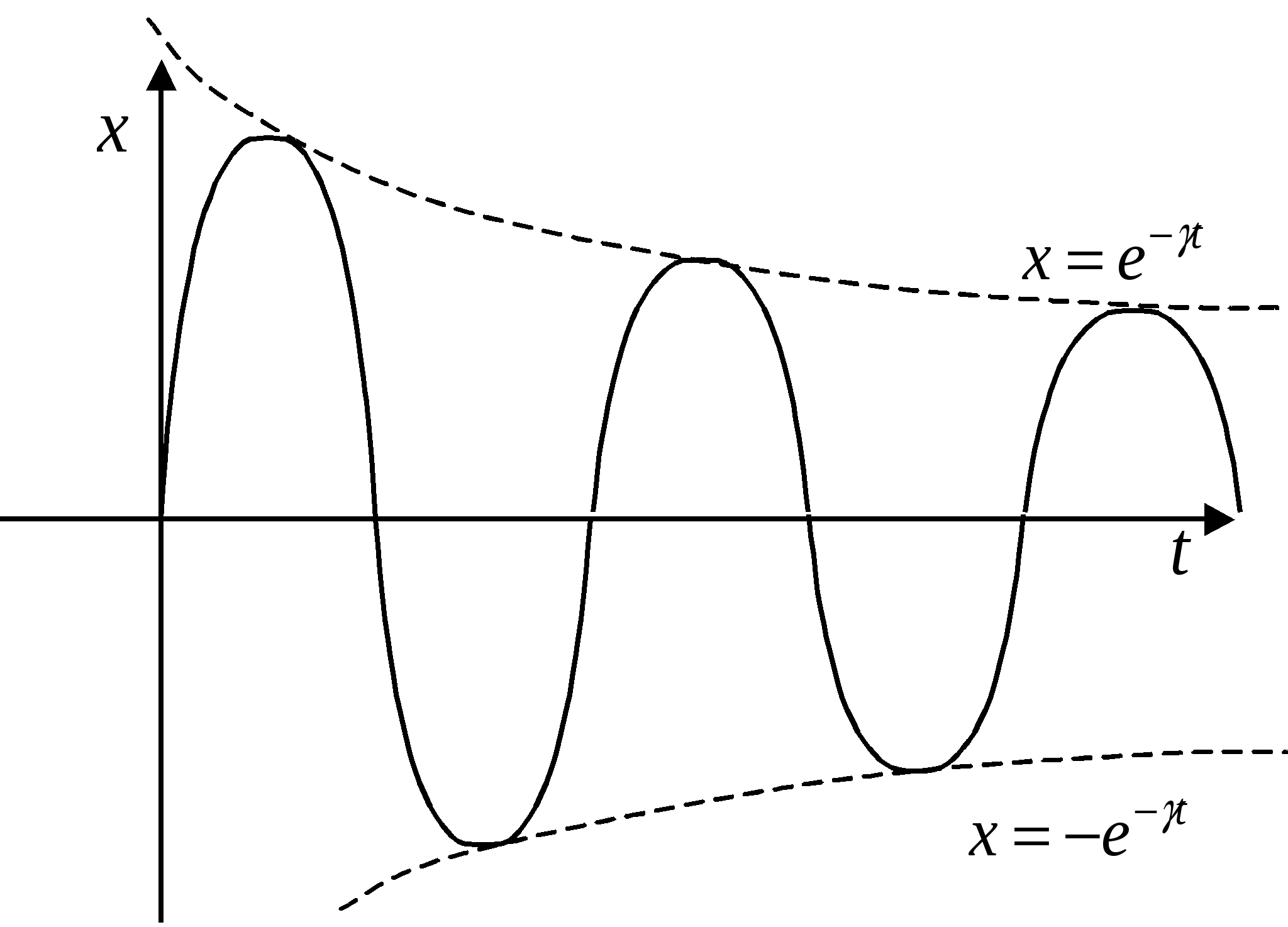 ремя релаксации – время, в течение которого значение параметра убывает в e раз: ремя релаксации – время, в течение которого значение параметра убывает в e раз: Декремент затухания характеризует, во сколько раз амплитуда колебаний убывает за один период: Логарифмический декремент затухания характеризует, во сколько раз изменяется логарифм убывания амплитуды: Пусть Скорость и ускорение затухающих колебаний: Добротность системы Э 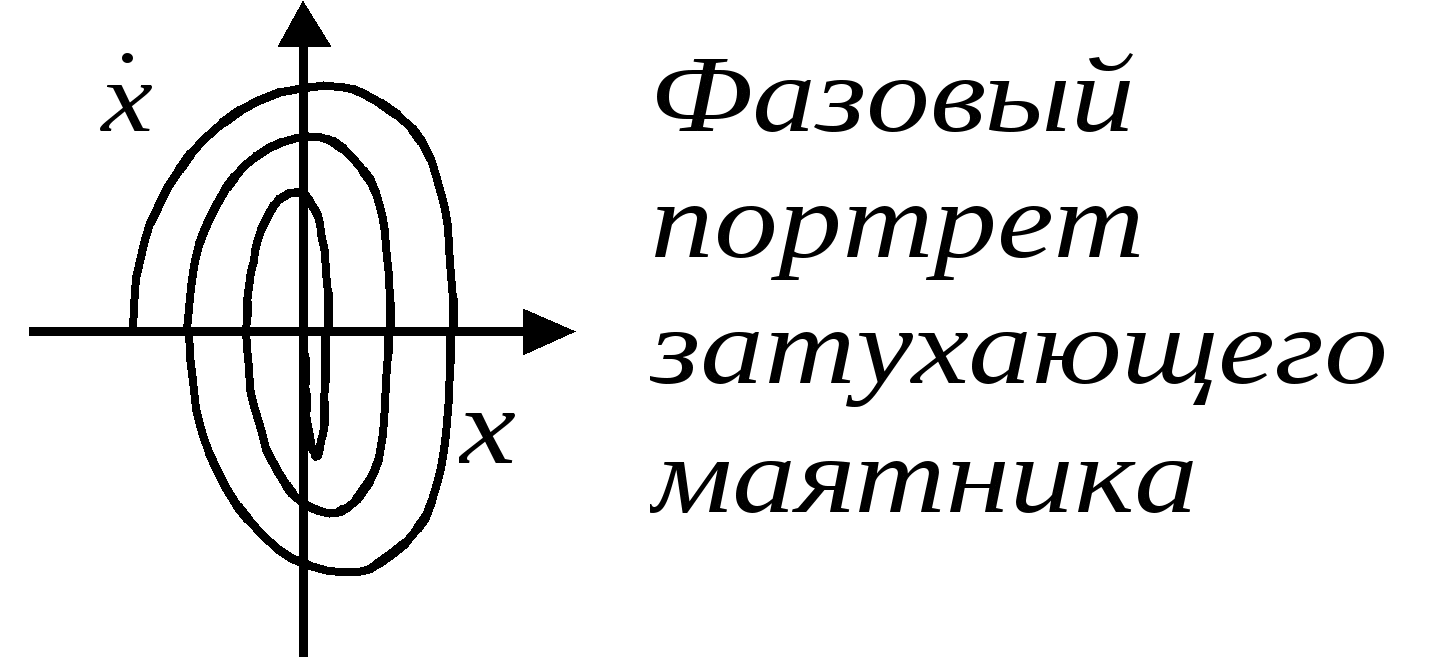 нергия нергия Вынужденные колебания Д  ля пружинного маятника: ля пружинного маятника: Для математического маятника: Длительность переходного режима совпадает со временем релаксации. Общее уравнение: 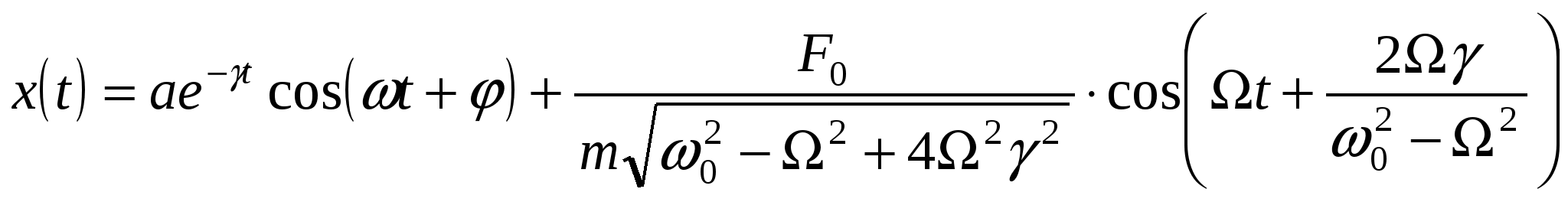 , где первое слагаемое представляет собой начальное колебаний системы, которое из-за затухания постепенно сходит на нет, а второе – установившийся режим вынужденных колебаний. , где первое слагаемое представляет собой начальное колебаний системы, которое из-за затухания постепенно сходит на нет, а второе – установившийся режим вынужденных колебаний.Резонанс. Н 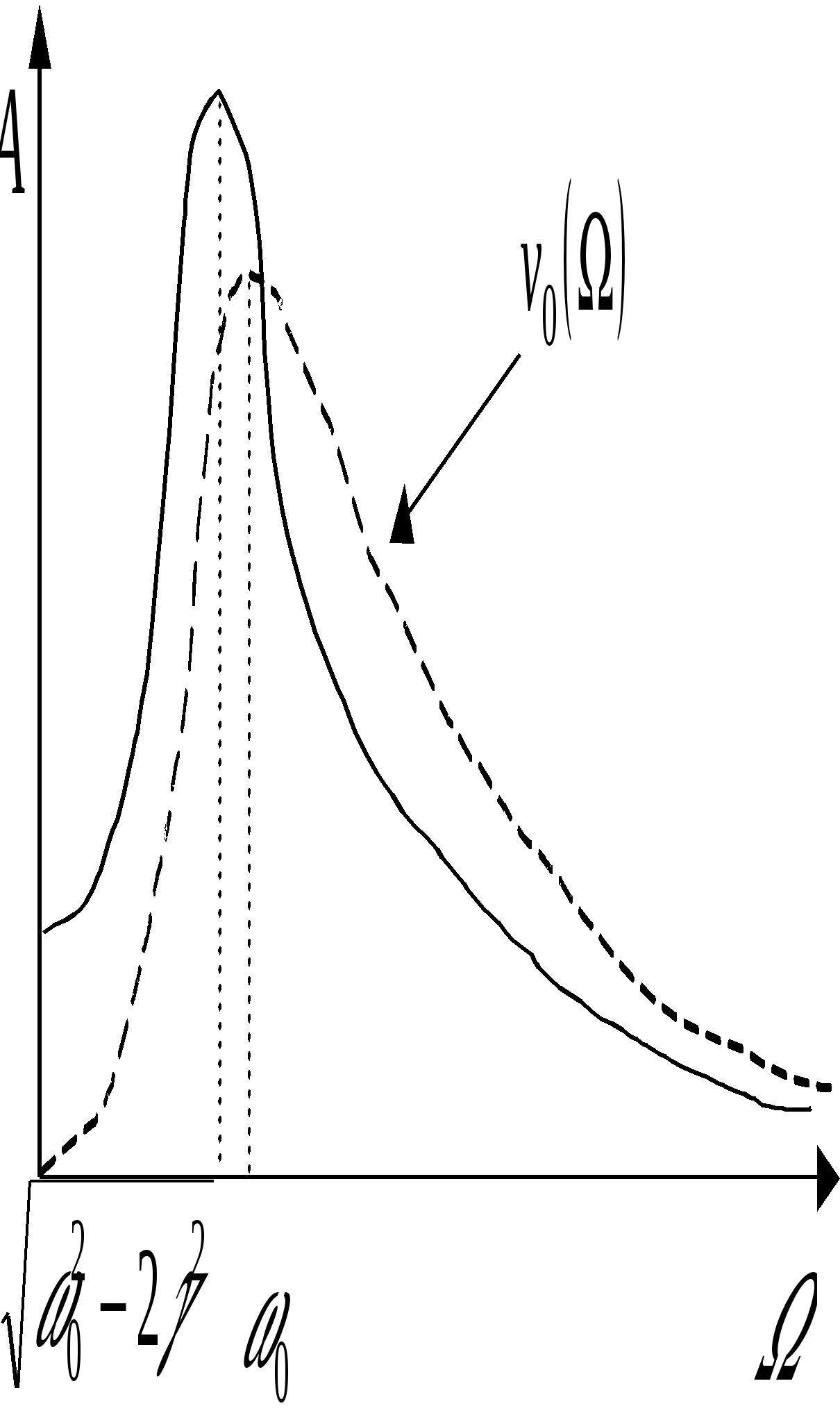 айдём максимум амплитуды колебаний в зависимости от частоты воздействующей силы. Для этого решим уравнение айдём максимум амплитуды колебаний в зависимости от частоты воздействующей силы. Для этого решим уравнение Резонанс – явление резкого возрастания (убывания) амплитуды вынужденных колебаний при стремлении частоты воздействия внешней силы к частоте собственных колебаний (точнее, к величине Резонансная частота – частота внешней возбуждающей силы, при которой достигается максимум амплитуды вынужденных колебаний. Наложение колебаний Сложение колебаний одного направления Пусть Векторная диаграмма:  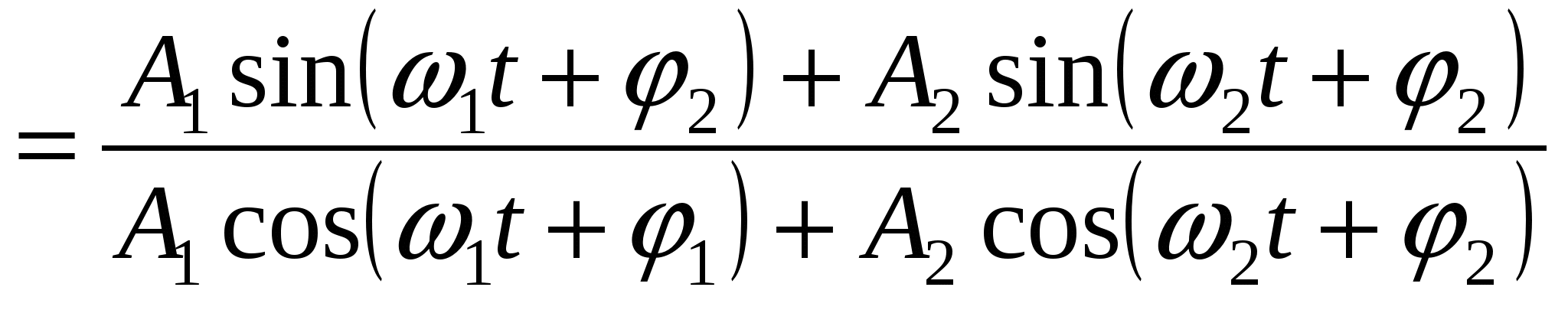 , , Таким образом, Б  иения: Рассмотри два колебания: иения: Рассмотри два колебания: Частота биения: Взаимно перпендикулярные колебания Рассмотрим два колебания, происходящие во взаимно перпендикулярных направлениях:
Фигура Лиссажу - эта линия, которую описывает тело, одновременно колеблющееся в двух взаимно перпендикулярных направлениях. Свойства фигур Лиссажу:
Механические волны Распространение волн в упругой среде Волны – процесс распространения колебаний в пространстве с течением времени. Упругие волны – волны, распространяющиеся в упругой среде. Волновая поверхность – геометрическое место точек среды, колеблющихся в одной фазе. Волновой фронт – поверхность, разделяющая возмущённую и невозмущённую части среды. Виды волн:
В газообразной и жидкой среде колеблется плотность или, что то же, давление. В твёрдой среде и на границе раздела фаз – деформация или, что то же, механическое напряжение. Волновое уравнение И 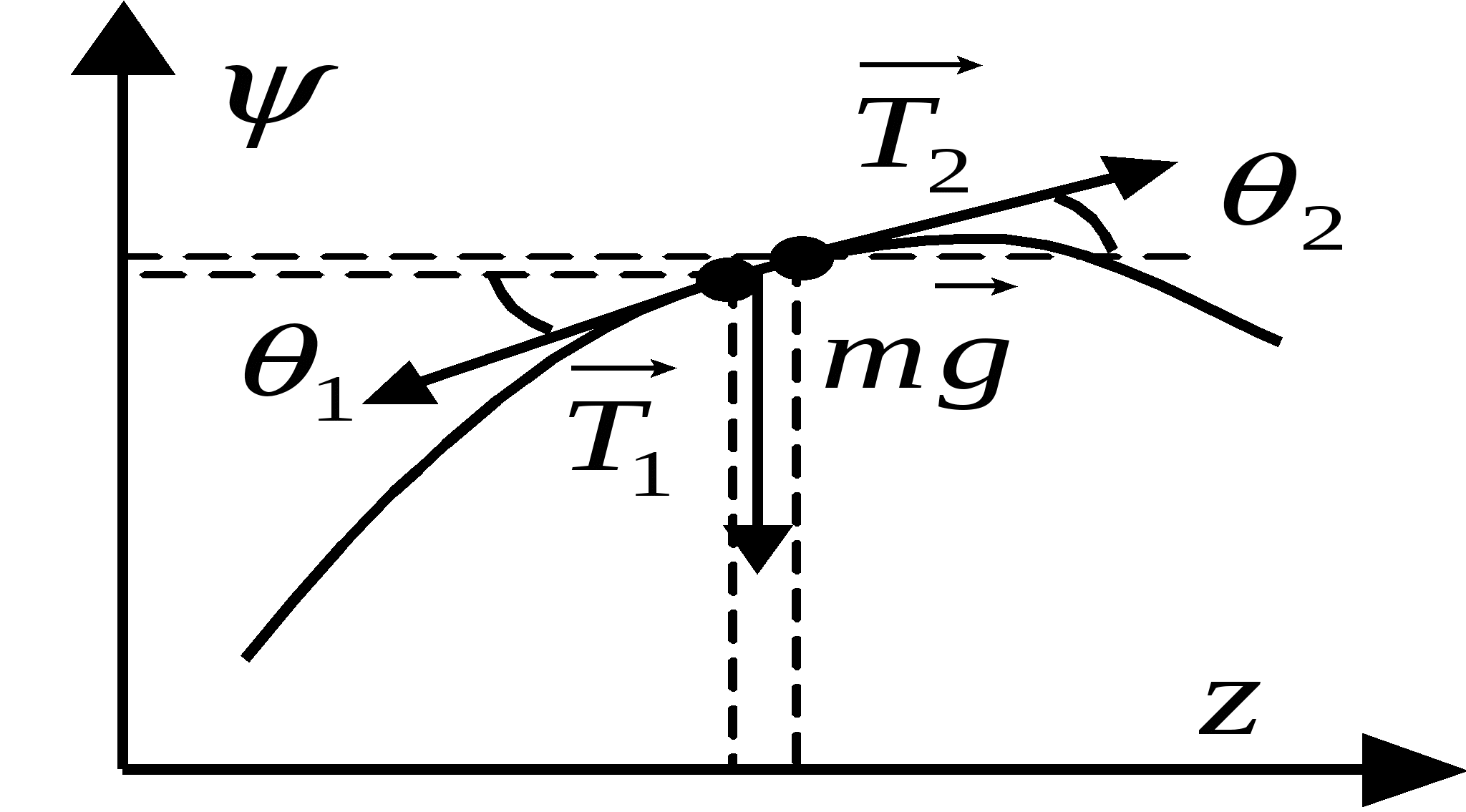 сследуем колебания струны. Пусть в какой-то момент времени струна деформирована так, как показано на рисунке. Тогда уравнение движения для этой струны выглядит так: сследуем колебания струны. Пусть в какой-то момент времени струна деформирована так, как показано на рисунке. Тогда уравнение движения для этой струны выглядит так: Волновое уравнение для продольной волны выглядит так: Анализ механических волн Пусть 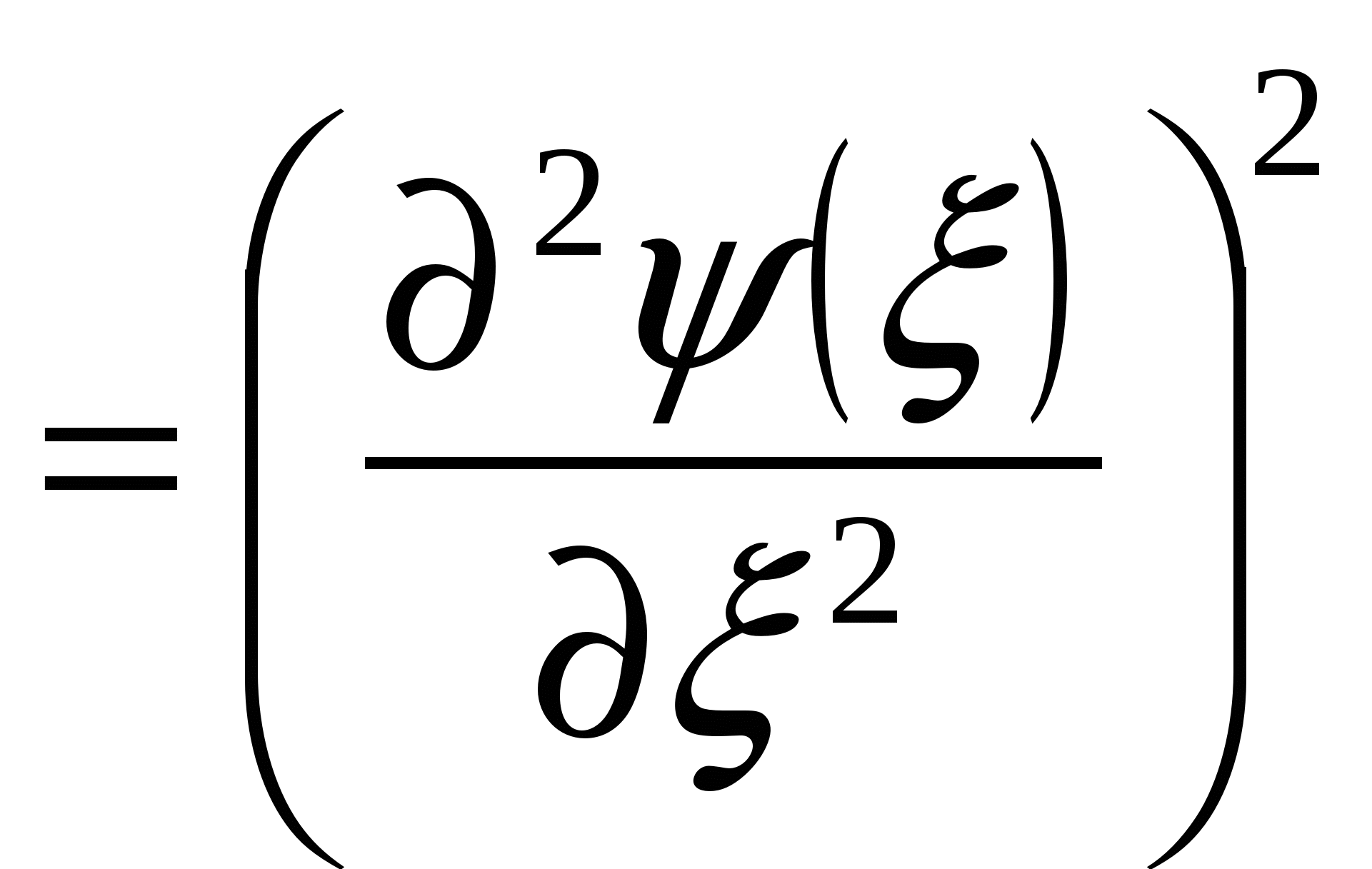 . .Общее решение волнового уравнения: Гармоническое решение волнового уравнения: Период волны Длина волны – расстояние, на которое распространяется волна за один период, Волновое число Волновой вектор: Фазовая скорость волны – скорость, с которой движутся точки волны, колеблющиеся в одной фазе. Геометрические свойства волн Для трёхмерного случая выражение Плоские, цилиндрические и сферические волны – волны, волновой фронт которых представляет собой соответственно плоскость, цилиндр и сферу. В случае плоской волны в волновом уравнении достаточно заменить Для цилиндрической волны Уравнение сферической волны: Бегущие и стоячие волны Если Рассмотрим сложение двух одинаковых волн, двигающихся навстречу друг другу. Т.е. пусть Узлы – это точки, амплитуда колебаний которых равна 0 (т.е. Пучности – это точки, амплитуда колебаний которых максимальна (т.е. Длина стоячей волны Граничные условия для стоячих волн:
Стоячие волны возбуждаются на струне или в акустической трубе только при соблюдении одного из этих условий. Основной тон – колебание с максимальной длиной волны: Энергия механической волны Скорость точек волны Рассмотрим волны на струне. Согласно закону Гука, Пусть Потоком энергии через поверхность называется энергия волны, проходящая через единицу времени через единичную поверхность, перпендикулярную вектору скорости волны: Интенсивность волны Эффект Доплера в акустике Эффект изменения частоты или длины волны, регистрируемой приёмником волн в сравнении с частотой или длиной волн, испущенной источником вследствие относительного движение приёмника и источника, называется эффектом Доплера. Пусть источник испускает волны с частотой
В общем случае 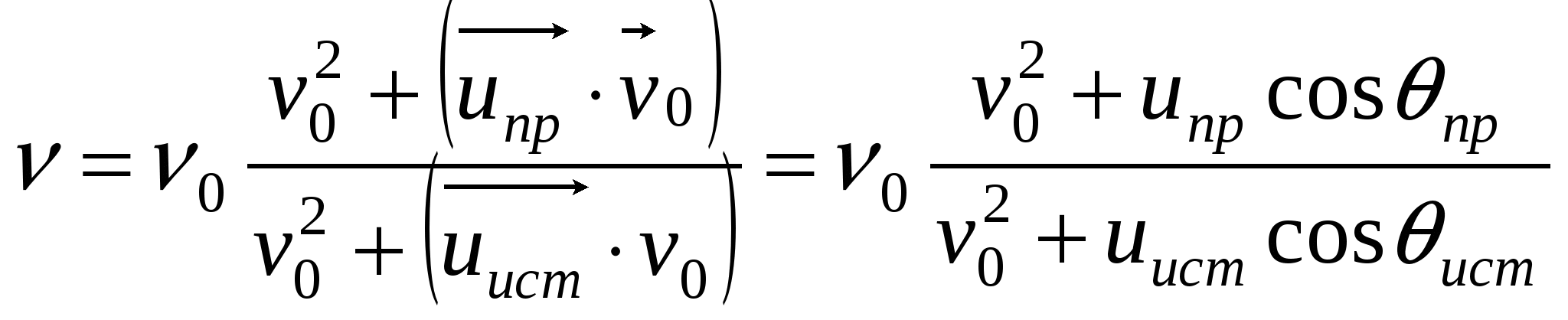 . . |

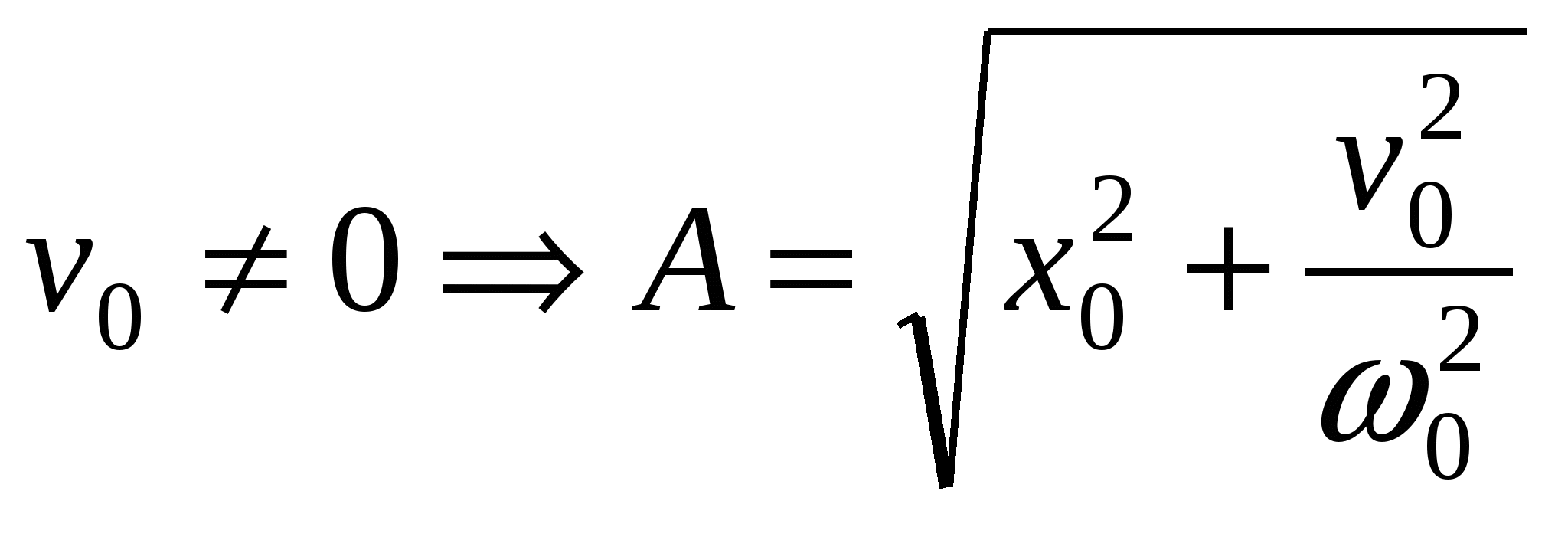 ,
, 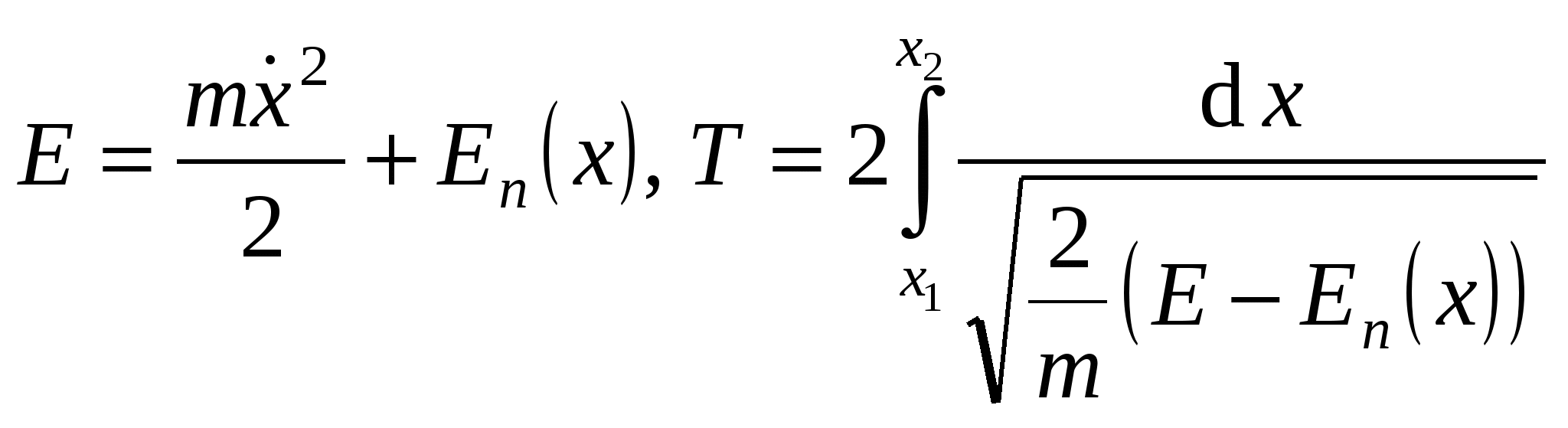 .
.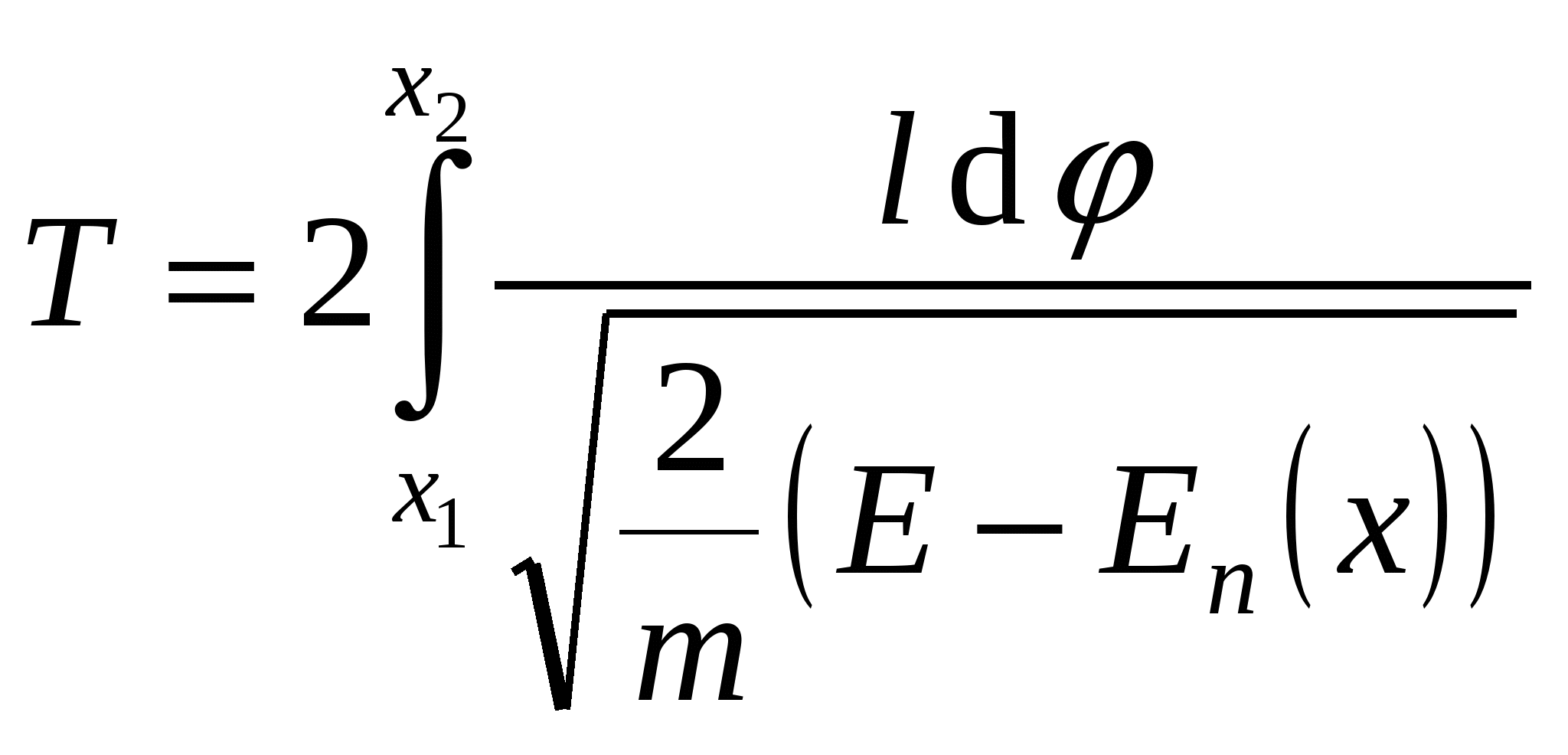 /
/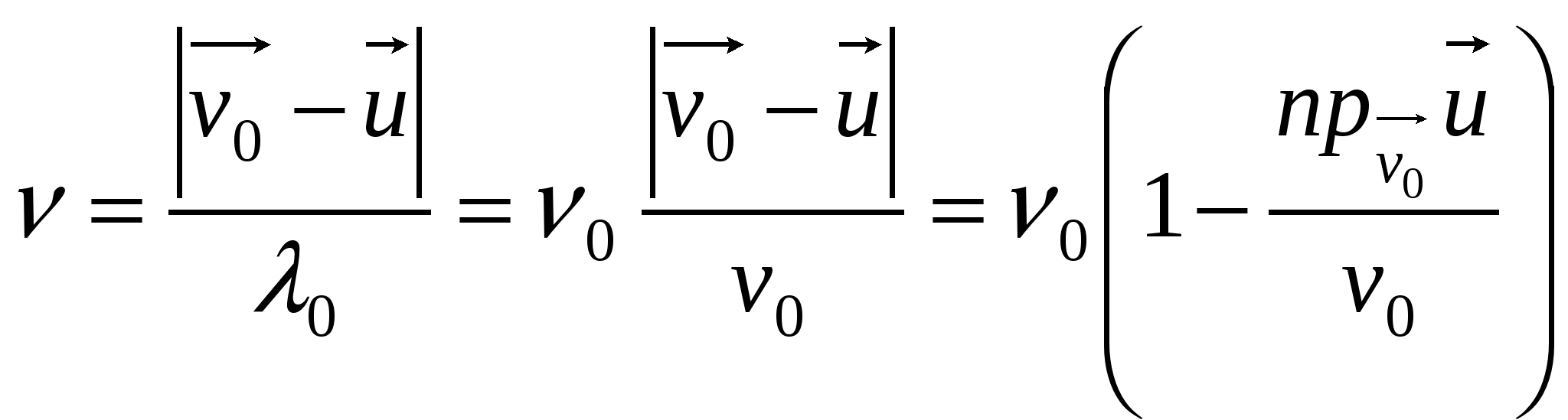 ,
, 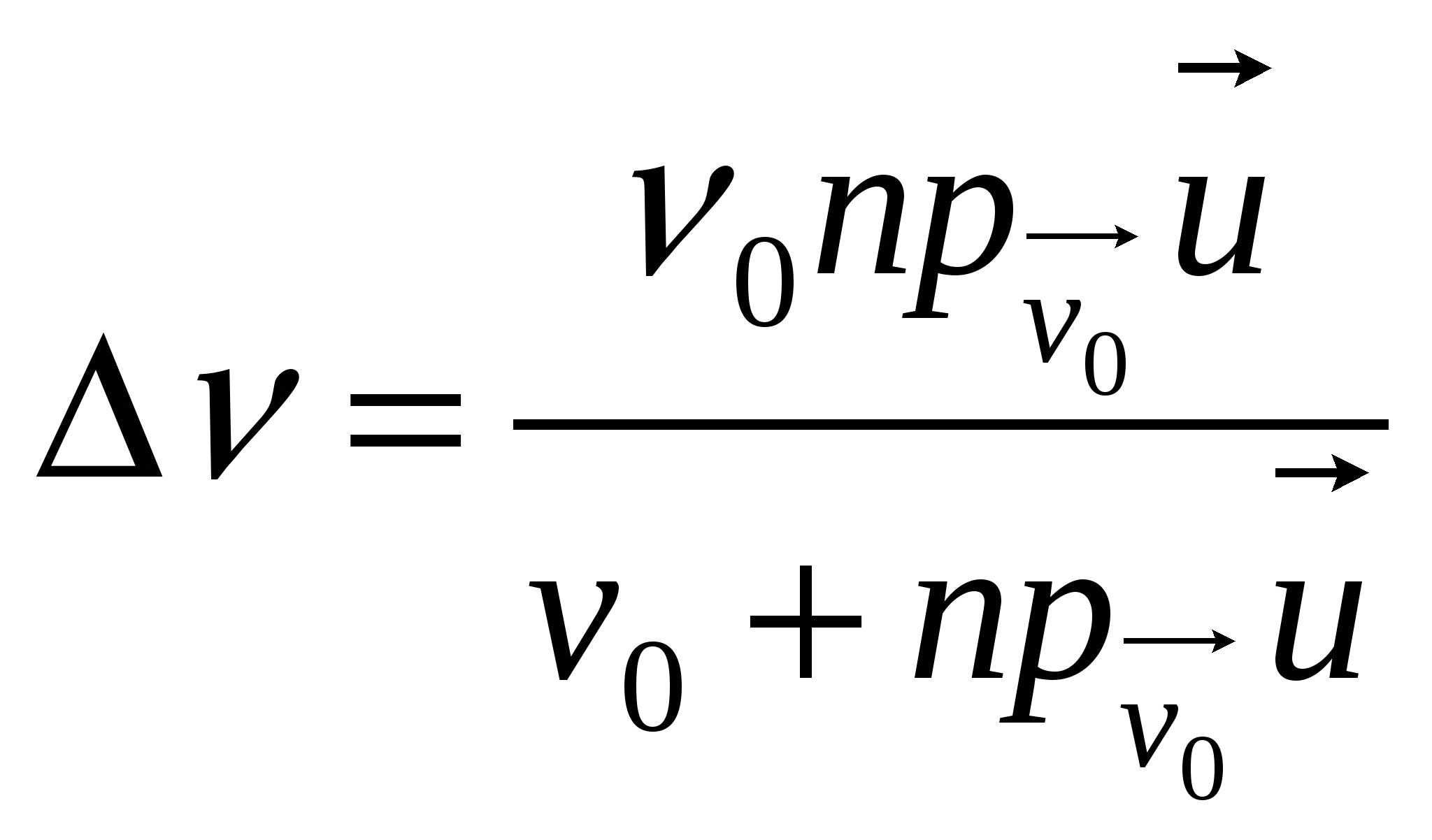 .
.