Математика. Мустакил иш copy. Механические приложения определенного интеграла. Интегрирование рациональных дробей
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ «МЭИ» в г. ТАШКЕНТЕ  Тема: Механические приложения определенного интеграла. Интегрирование рациональных дробей. студента группы 20-21 УТС Собировой Хадичабону Принял: ______________ ст.преп. 2022 Тема: Механические приложения определенного интеграла. Интегрирование рациональных дробей. План: Введение Работа переменной силы, Путь, пройденный телом. Вычисление статических моментов и координат центра тяжести плоской кривой. Вычисление статических моментов и координат центра тяжести плоской фигуры Интегрирование рациональных дробей. Заключение Литература Введение Нахождение производной f’(x) или дифференциала df=f’(x)dx функции f(x) является основной задачей дифференциального исчисления. В интегральном исчислении решается обратная задача: по заданной функции f(x) требуется найти такую функцию F(x), что F’(х)=f(x) или F(x)=F’(x)dx=f(x)dx.. Таким образом, основной задачей интегрального исчисления является восстановление функции F(x) по известной производной (дифференциалу) этой функции. Интегральное исчисление имеет многочисленные приложения в геометрии, механике, физике и технике. Оно дает общий метод нахождения площадей, объемов, центров тяжести и т. д. Задача о нахождении площади Определить площадь P криволинейной трапеции ABCD (рис 1)  Рис 1 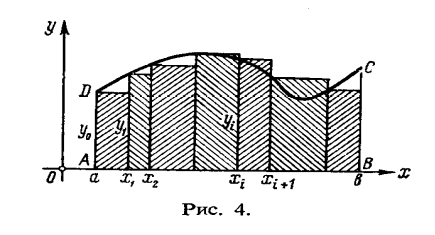 Разделим основание АВ нашей фигуры произвольным образом на части и проведем ординаты, соответствующие точкам деления; тогда криволинейная трапеция разобьется на ряд полосок. Заменим теперь приближенно каждую полоску некоторым прямоугольником, основание которого то же, что и у полоски, а высота совпадает с одной из ординат полоски, скажем с крайней слева. Таким образом, криволинейная фигура заменится некоторой ступенчатой фигурой, составленной из отдельных прямоугольников. Обозначим абсциссы точек деления через  X X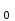  = a < X = a < X < X < X < … < X < … < X < X < X < … < X < … < X = b. = b.Основание i – го прямоугольника равно разности X  - X - X (ΔX (ΔX ). Высота равна y ). Высота равна y = f (X = f (X ). Поэтому площадь i – го прямоугольника будет y ). Поэтому площадь i – го прямоугольника будет y ΔX ΔX = f (X = f (X ) ΔX ) ΔX . .Просуммировав площади всех прямоугольников, получим приближенное значение площади P криволинейной трапеции P=  y y ΔX ΔX или P= или P= f (X f (X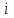 ) ΔX ) ΔX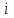 . .Погрешность этого равенства при безграничном убывании всех ΔX 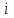 стремится к нулю. Точное значение площади P получится как предел: стремится к нулю. Точное значение площади P получится как предел:P=Lim 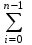 y y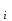 ΔX ΔX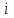 или P=Lim или P=Lim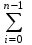 f (X f (X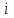 ) ΔX ) ΔX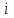 , ,В предположении, что все ΔX 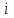 одновременно стремятся к 0. одновременно стремятся к 0.Для обозначения предельного значения суммы 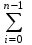 y ΔX Лейбниц и ввел символ ∫ ydx, где ydx напоминает типичное слагаемое суммы, а ∫ есть стилизованная буква S - начальная буква латинского слова “Summa”. Так как площадь, представляющая это предельное значение, в то же время является первообразной для функции у, то тот же символ сохранился и для обозначения первообразной функции. Впоследствии, с введением функционального обозначения, стали писать y ΔX Лейбниц и ввел символ ∫ ydx, где ydx напоминает типичное слагаемое суммы, а ∫ есть стилизованная буква S - начальная буква латинского слова “Summa”. Так как площадь, представляющая это предельное значение, в то же время является первообразной для функции у, то тот же символ сохранился и для обозначения первообразной функции. Впоследствии, с введением функционального обозначения, стали писать∫ f(x)dx, если речь идет о переменной площади, и 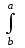 f(x)dx, f(x)dx,- в случае площади фиксированной фигуры ABCD, отвечающей изменению х от а до b. Определение. Пусть функция f (X  ) задана в некотором промежутке [a, b].Разобьем этот промежуток произвольным образом на части, вставив между aи bточки деления. Наибольшую из разностей ΔX ) задана в некотором промежутке [a, b].Разобьем этот промежуток произвольным образом на части, вставив между aи bточки деления. Наибольшую из разностей ΔX = X = X - X - X (i = 0, 1,2, . ..,n-1) обозначим через λ. (i = 0, 1,2, . ..,n-1) обозначим через λ.Возьмем в каждом из частичных промежутков [X  , X , X ] по произволу точку X = ξ ] по произволу точку X = ξ X  ≤ξ ≤ξ ≤ X ≤ X (i = 0, 1, … , n-1) (i = 0, 1, … , n-1)и составим сумму σ =  f(ξ f(ξ ) ΔX ) ΔX Пусть I конечный предел данной суммы I =  σ. σ.Конечный предел I суммы σ при  называется определенным интегралом функции f(x) в промежутке от a до b и обозначается символом называется определенным интегралом функции f(x) в промежутке от a до b и обозначается символом I =  f(x)dx f(x)dxВ случе существования такого предела функция f(x) называется интегрируемой в промежутке [a, b]. Числа a и b носят название, соответственно, нижнего и верхнего пределов интеграла. При постоянных пределах определенный интеграл представляет собой постоянное число. Приведенное определение принадлежит Риману (B.Riemann), коорый впервые высказал его в общей форме и исследовал область его применения.[7] Механические приложение определенного интеграла Работа переменной силы Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F = F(х), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (а <bЬ), находится по формуле A = 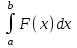 Пример. Какую работу нужно затратить, чтобы растянуть пру-'—' жину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?[5] Решение: По закону Гука упругая сила, растягивающая пружину, пропорциональна этому растяжению х, т. е. F = kх, где k— коэффициент пропорциональности. Согласно условию задачи, сила F = 100 Н растягивает пружину на х = 0,01 м; следовательно, 100 = k 0,01, откуда k = 10000; следовательно, F =10000х. Искомая работа на основании формулы A = 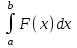 равна A =  П  ример.Найти работу, которую необходимо затратить, чтобы выкачать через край жидкость из вертикального цилиндрического резервуара высоты Н м и радиусом основания Rм (рис 13).[5] ример.Найти работу, которую необходимо затратить, чтобы выкачать через край жидкость из вертикального цилиндрического резервуара высоты Н м и радиусом основания Rм (рис 13).[5] Рис 13 Решение: Работа, затрачиваемая на поднятие тела весом р на высоту h, равна р • Н. Но различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия (до края резервуара) различных слоев не одинакова. Для решения поставленной задачи применим схему II (метод дифференциала). Введем систему координат. 1. Работа, затрачиваемая на выкачивание из резервуара слоя жидкости толщиной х (0 ≤ х ≤ Н), есть функция от х, т. е. А = А(х), где (0 ≤ х ≤ Н)( A(0) = 0, A(H) = А0). 2. Находим главную часть приращения ΔA при изменении х на величину Δх = dx, т. е. находим дифференциал dА функции А(х). Ввиду малости dх считаем, что “элементарный” слой жидкости находится на одной глубине х (от края резервуара). Тогда dА = dрх, где dр — вес этого слоя; он равен g 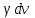 АV, где g — ускорение свободногопадения, АV, где g — ускорение свободногопадения, 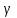 — плотность жидкости, dv— объем “элементарного” слоя жидкости (на рисунке он выделен), т. е. dр = g — плотность жидкости, dv— объем “элементарного” слоя жидкости (на рисунке он выделен), т. е. dр = g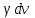 . Объем указанного слоя жидкости, очевидно, равен . Объем указанного слоя жидкости, очевидно, равен 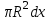 , где dx— высота цилиндра (слоя), , где dx— высота цилиндра (слоя),  — площадь его основания, т. е. dv= — площадь его основания, т. е. dv=  . .Таким образом, dр =  .и .и  3) Интегрируя полученное равенство в пределах от х = 0 до х = Н, находим A 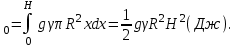 Путь, пройденный телом Пусть материальная точка перемещается по прямой с переменной скоростью v=v(t). Найдем путь S, пройденный ею за промежуток времени от t 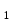 до t2. до t2. Решение: Из физического смысла производной известно, что при движении точки в одном направлении “скорость прямолинейного движения равна производной от пути по времени”, т. е. v(t) = 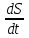 . Отсюда следует, что dS = v(t)dt. Интегрируя полученное равенство в пределах от t . Отсюда следует, что dS = v(t)dt. Интегрируя полученное равенство в пределах от t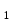 до t до t , ,получаем S =  Пример.Найти путь, пройденный телом за 4 секунды от начала движения, если скорость тела v(t)= 10t + 2 (м/с).[5] Решение: Если v(t) = 10t + 2 (м/с), то путь, пройденный телом от начала движения (t = 0) до конца 4-й секунды, равен S =  Давление жидкости на вертикальную пластинку По закону Паскаля давление жидкости на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием пластинку, а высотой — глубину ее погружения от свободной поверхности жидкости, т. е. Р =g  , где g — ускорение свободного падения, , где g — ускорение свободного падения,  — плотность жидкости, S — площадь пластинки, h — глубина ее погружения. — плотность жидкости, S — площадь пластинки, h — глубина ее погружения.По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах. Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, y  и y и y . Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала). . Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала). 1. Пусть часть искомой величины Р есть функция от х: р = р(х), т. е. р = р(х) — давление на часть пластины, соответствующее отрезку [а; b]значений переменной х, где х 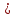 [a; b] (р(a) = 0, р(b) = Р). [a; b] (р(a) = 0, р(b) = Р). Рис 14 2. Дадим аргументу х приращение Δx = dх. Функция р(х) получит приращение Δр (на рисунке — полоска-слой толщины dх). Найдем дифференциал dр этой функции. Ввиду малости dх будем приближенно считать полоску прямоугольником, все точки которого находятся на одной глубине х, т. е. пластинка эта — горизонтальная. Тогда по закону Паскаля dр = 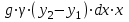 . .3. Интегрируя полученное равенство в пределах от х = а до х = b, получим P = 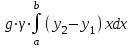 или P = или P = 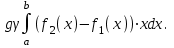 Пример. Определить величину давления воды на полукруг, вертикально погруженный в жидкость, если его радиус R, а центр О находится на свободной поверхности воды (рис 15).[5] Решение: Воспользуемся полученной формулой для нахождения давления жидкости на вертикальную пластинку. В данном случае пластинка ограничена линиями у 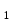 = - = -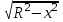 , y , y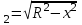 , x = 0, x = R. , x = 0, x = R. P 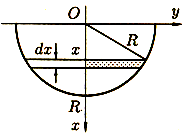 = =     Рис 15  Вычисление статических моментов и координат центра тяжести плоской кривой Пусть на плоскости Оху задана система материальных точек М 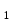 (х (х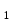 ;у ;у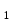 ), М2(х2;y ), М2(х2;y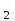 ), … , M ), … , M (x (x ;y ;y ) соответственное массами m ) соответственное массами m ,m ,m , … , m„. , … , m„.Статическим моментом SХсистемы материальных точек относительно оси Ох называется сумма произведений масс этих точек на их ординаты (т. е. на расстояния этих точек от оси Ох):  Аналогично определяется статистический момент S  этой системы относительно оси Oy: S этой системы относительно оси Oy: S = = 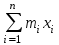 . .Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование. Пусть у =f/(х) (a ≤ х ≤ b) — это уравнение материальной кривой АВ. Будем считать ее однородной с постоянной линейной плотностью 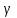 ( (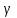 = const). = const).Для произвольного х 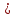 [а;b]на кривой АВ найдется точка с координатами (х; у). Выделим на кривой элементарный участок длины dl, содержащий точку (х;у). Тогда масса этого участка равна [а;b]на кривой АВ найдется точка с координатами (х; у). Выделим на кривой элементарный участок длины dl, содержащий точку (х;у). Тогда масса этого участка равна  . Примем этот участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у. Тогда дифференциал статического момента dS . Примем этот участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у. Тогда дифференциал статического момента dS (“элементарный момент”) будет равен (“элементарный момент”) будет равен  , т.е. , т.е.  . .Отсюда следует, что статический момент SХкривой АВ относительно оси Ох равен  Аналогично находим S  : : Статические моменты SХи SУкривой позволяют легко установить положение ее центра тяжести (центра масс). Центром тяжести материальной плоской кривой у = f(х), х 6 [а; b] называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу т заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой у = f(х) относительно той же оси. Обозначим через С(хс;ус) центр тяжести кривой АВ. Из определения центра тяжести следуют равенства  и и  или или  и и  . Отсюда . Отсюда  , ,  или    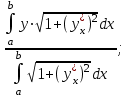 Пример.Найти центр тяжести однородной дуги окружности x 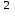 + y + y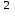 =R2, расположенной в первой координатной четверти (рис 16).[5] =R2, расположенной в первой координатной четверти (рис 16).[5] Рис 16 Р 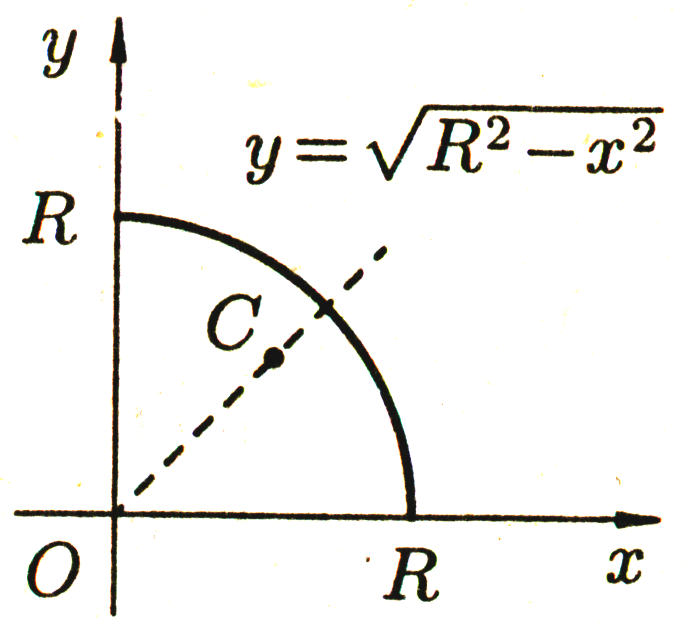 ешение: Очевидно, длина указанной окружности равна ешение: Очевидно, длина указанной окружности равна  , т.е. , т.е.  . Найдем статистический момент ее относительно оси Ох. Так как уравнение дуги есть . Найдем статистический момент ее относительно оси Ох. Так как уравнение дуги есть  и и  , то ( , то ( ) )  . .Стало быть,  Так как данная дуга симметрична относительно биссектрисы первого координатного угла, то хс = ус =  Итак, центр тяжести имеет координаты ( Итак, центр тяжести имеет координаты ( ; ; ). ).Вычисление статических моментов и координат центра т  яжести плоской фигуры яжести плоской фигурыПусть дана материальная плоская фигура (пластинка), ограниченн кривой у = f(х) ≥ 0 и прямыми у = 0, х = а, х = b) (рис 17). Будем считать, что поверхностная плотность пластинки постоянна ( 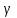 = const). Тогда масса всей пластинки равна = const). Тогда масса всей пластинки равна 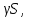 т. е. т. е. 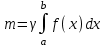 . Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником. . Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.Тогда масса его равна 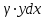 . Центр тяжести . Центр тяжести 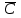 прямоугольника лежит на пересечении диагоналей прямоугольника. Эта точка прямоугольника лежит на пересечении диагоналей прямоугольника. Эта точка 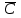 отстоит от оси Ох на ½y, а от оси Оу на x (приближенно; точнее на расстоянии х+ ½Δx). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения отстоит от оси Ох на ½y, а от оси Оу на x (приближенно; точнее на расстоянии х+ ½Δx). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения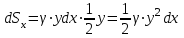 и и 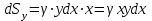 Следовательно, 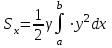 , , 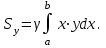 По аналогии с плоской кривой получаем, обозначив координаты центра тяжести плоской фигуры (пластинки) через С(x 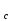 ;y ;y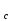 ), что ), что 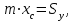 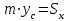 . .Отсюда 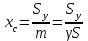 и и 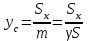 или x 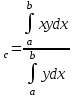 , ,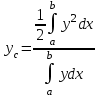 . .П 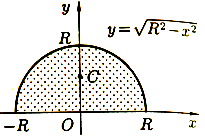 ример. Найдем координаты центра тяжести полукруга ример. Найдем координаты центра тяжести полукруга 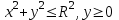 ( ( = const) (рис 18). = const) (рис 18).  Рис 18  [5] [5]Решение: Очевидно (ввиду симметрии фигуры относительно оси Oy), что  . Площадь полукруга равна . Площадь полукруга равна  . Находим Sx: . Находим Sx:  Стало быть,  Итак, центр тяжести имеет координаты С(0;  ) )Интегрирование рациональных дробей Рациональной дробью называется отношение двух многочленов  . .Рациональная дробь называется правильной, если степень многочлена  ниже степени многочлена ниже степени многочлена  ; в противном случае дробь называется неправильной. ; в противном случае дробь называется неправильной.Если дробь неправильная, то следует выделить целую часть, т.е. представить ее в виде суммы многочлена и правильной дроби. Простейшими дробями называют правильные дроби четырех видов:  В случаях III и IV квадратный трехчлен не имеет действительных корней.   Интегрированию дробей III типа посвящен предыдущий пункт. Любую правильную дробь можно разложить на сумму простейших дробей. Для этого знаменатель раскладывают на линейные и квадратичные множители так, чтобы квадратичные не имели вещественных корней. Рассмотрим три важных случая. 1.  раскладывается на линейные различные множители. Дробь представима в виде суммы n простейших дробей 1 типа. раскладывается на линейные различные множители. Дробь представима в виде суммы n простейших дробей 1 типа.  2. Каждому линейному множителю кратности k, соответствует (k-1) дробей 2 типа и одна дробь 1 типа  3. Каждому квадратичному множителю  соответствует дробь III типа соответствует дробь III типа Коэффициенты Случай, когда знаменатель содержит квадратичные кратные множители, мы не рассматриваем. Пример 1. Найти интеграл  Решение. Под знаком интеграла неправильная дробь. Выделим целую часть, разделив числитель дроби на знаменатель:       Следовательно, Следовательно,   – – Пример 2. Найти интеграл  Решение. Подынтегральная функция – правильная дробь. Представим ее в виде суммы простейших дробей   Найдем коэффициенты разложения методом частных значений. Полагая в полученном тождестве вместо  Подставив в равенство (1) найденные значения коэффициентов, имеем:   Пример 3. Найти интеграл  Решение.     Приравнивая коэффициенты при  получаем: получаем:  Пример 4. Найти интеграл  Решение.  . .Приводя правую часть к общему знаменателю и приравнивая числители, получим:  . .Комбинируя методы частных значений и сравнивая коэффициенты, найдем: 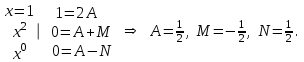 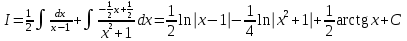 . .Заключение Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости. Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности. Так в процессе выполнения курсовой работы нами были рассмотрены примеры практических задач в области физики, геометрии, механики, биологии и экономики. Конечно, это еще далеко не исчерпывающий список наук, которые используют интегральный метод для поиска устанавливаемой величины при решении конкретной задачи, и установлении теоретических фактов. Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл - это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения. Из всего выше сказанного понятно, почему знакомство с определенным интегралом происходит еще в рамках средней общеобразовательной школы, где ученики изучают не только понятие интеграла и его свойства, но и некоторые его приложения. Дальнейшая наша работа над данной темой планируется именно в направлении рассмотрения методики и линий изучения определенного интеграла в школе. Литература Баврин И.И. Высшая математика – М.: Просвещение, 1993. – 319. Бермантт А.Ф. , Араманович И.Г. Краткий курс математического анализа для втузов - М.: Наука, 1971 . - 736с. Красс М.C Основы математики и ее приложения в экономическом образовании Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, Том 2 -М. :Наука, 1985.-560с. Письменный Д.Т. Конспект лекций по высшей математике – M.: Айрис – пресс, 2003. – 288 c. Солодовников А.С., Бабайцев В.А Математика в экономики – M.: Финансы и статистика, 2005. – 560c. Фихтенгольц Том 2 Шипачёв В.С. Высшая математика - М: Наука, 2003 – 684c. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах - ч.I, II – М.: Высшая школа, 1986. Кузнецов Л.А. Сборник задач по высшей математике (типовые расчеты) – М.: Высшая школа, 1983. Шипачев В.С. Высшая математика. М.: Высшая школа, 1990. |
