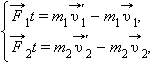билеты по физике. Механическое движение
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
|
БИЛЕТ 8 1) работа силы- мера действия силы при превращении механического движения в другую форму движения. A=F*Scosa примеры формул работы сил: работа силы тяжести: A=mgh Работа силы тяжести по наклонной поверхности: A=mgscosa Работа силы упругости: A=kx^2/2 A=k/2 (x1^2-x2^2) Работа силы трения: A=-|F(вектор)|s Консервативными называются силы, работа которых не зависит от формы траектории. Определяется только положеним начальных и конечных точек. К калссу консервативных сил относят гравитационные силы, упругие и силы электростатического взаимодействия. Существуют силы, работа которых зависит от формы пути. То есть работа по замкнутой траектории не равна 0, например сила трения. Такие силы называются неконсервативными. В этом случае работа не идет на увеличение потенциальной энергии, а идет на увеличение кинетической энергии молекул тела( на нагревание. Потенциальная энергия – скалярная физическая величина, равная работе, совершаемой потенциальной силой при перемещении тела из данной точки в точку, потенциальная энергия которой принято за ноль. Eп=mgh – потенциальная энергия взаимодействия тела и земли Eп=-G*Mm/r - Потенциальная энергия тел, взаимодействующих по средствам гравитационных сил. Eп= (kx^2)/2- Потенциальная энергия упруго деформированного тела. Работа силы упругости. Связь потенциальной энергии с силой взаимодейстия: F=-grad*Eп Градиент – вектор показывающий направление наибыстрейшего изменения функции. 2) Интерференция света – устойчивое во времени усиление интенсивности света в одних точках пространства, ослабление – в других, наблюдаемое при наложении когерентных волн. Когерентные волны – разность фаз колебаний, возбуждаемых ими в какой либо точке, остается постоянной во времени, одиннаковая частота колебаний, колебание кетора E вдоль одной одной прямой или вдоль параллельных прямых ( могут быть только монохроматические волны) Монохроматическая волна – волна одной определенной и строго постоянной частоты. к-волновое число, показывающее чему равна разность фаз точек, находящихся на расстоянии 1м. r – расстояние до точки E1=E01sin(омегаt-k1r1) E2=E02sin(омегаt-k2r2) K1=2Pi/лямбда1 K2=2Pi/лямбда2 d<<L В точке M складываются два колебания одной частоты и одного направления. E0^2(результ)=E01^2+E02^2+2E01E02cosdeltaфи deltaфи = k1r1-k2r2 лямбда=VT = cT/n1=лямбданулевое/n1 Vср= c/n n- коэф преломления. Deltaфи= 2Pi*deltaб/лямбда нулевое (б- сигма маленькая, только в другую сторону) лямбданулевое - длина волны в вакууме. б=nr – оптическая длина пути deltaб=n1r1-n2r2 – разность оптических путей – связь разности оптических длин путей волн с разностью фаз колебаний, вызываемых волнами. Оптическая длина пути между двумя точками среды — расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения между этими точками. Условия максимумов и минимумов амплитуды при интерференции двух волн. E0^2(результ)=E01^2+E02^2+2E01E02cosdeltaфи Iрезультирующее = I1+I2+2sqrt(I1*I2) cosфи delta фи = const – когерентные волны deltaфи не равно const – не когерентные волны, косинус фи =0 Iрезульт = I1+I2 – интерференции не будет. Cosdeltaфи=1 deltaфи=+-2PiN, где n=1 2 3 …. Deltaфи= (2Pi/лямбданулевое)*deltaб условие максимум: deltaб=+-Nлямбданулевое Амплитуда результирующего колебания будет максимальной и равной E01+E02, если разность оптических путей волн равна целому числу длин волн в вакууме. Cosфи=-1 deltaфи= +-(2N+1)Pi, N = 0 1 2 3 ….. Условие минимума: deltaб=+-(2N+1) лямбданулевое/2 Амплитуда результирующего колебания будет минимальной и равной разности амплитуд, если разность оптических путей равна полуцелому числу длин волн. Интерференционные полосы и интерференционная картина на плоском экране при освещении двух узких длинных параллельных щелей. А)красным светом Б) белым светом. Опыт Юнга а) если используется монохроматический свет, то на экране увидим чередование светлых и темных полос данного цвета. С увеличением порядка кольца интенсивность уменьшается. Полосы тусклеют. Б) если источник дает белый свет, то на экране в области светлых полос наблюдается радужные полосы. Радужность объясняется тем, что условия максимумов и минимумов зависит от длины волны. 3) Тепловое излучение, его энергетические характеристики. Тепловое излучение – электромагнитное излучение, испускаемое телом за счет его внутренней энергии, присущей всем телам при всех температурах. С увеличением температуры: 1)увеличивается интенсивность излучения. 2) максимум излучения смещается в сторону более коротких длин волн. 3) температура тела понижается, пока не наступит термодинамическое равновесие. Энергетические характреистики теплового излучения. 1) поток энергии( мощность излучения) Ф=dW/dt (Вт) dW – энергия теплового излучения всех длин волн испускаемого за время dt. 2) Энергетическая светимость: M=dФ/dS (Вт/м^2), где М – энергетическая светимость. М= потоку энергии всех длин волн, которые испускаются единицей поверхности. M=W/St , где М численно равна энергии всех длин волн, излучаемых телом с единицы площади за единицу времени. М=f(t) - хар. Интенсивность излучения при данной t 3) cпектральная плотность энергетической светимости. Mλ = dM/d λ Mν=dM/dν ….. Mλ численно равна энергии электромагнитных волн с длинами от лямбда до лямбда +dлямбда испускаемых с единицы площади за единицу времени и отнесенной к ширине интервала dлямбда. Mλ=f(T, λ) - характеризует интенсивтность телпового излучения для данных Т и лямбда. M= интеграл от нуля до бесконечности Mλdλ 4) Коэффициент поглощения ( поглощательная способность) αλ=dФ(погл) λ/dФ(падающего) λ, где αλ<=1 Альфалямбда показывает какая часть энергии падающего потока данной длины волны поглощается поверхностью тела. альфалямбда=1 – абсолютно черное тело. ЗАКОНЫ кирхгофа: Mλ1/ αλ1= Mλ2/ αλ2=…….= Mλ0. Mλ0=f(лямбда, T) - функция кирхгофа.(спектральная плотность энергетичской светимости абсолютно черного тела. Отношение мпектральной плотности энергетической светимости тела к его коэфу поглощения одиннаково для всех тел и равно спектральной плотности энергетической светимости абсолютно черного тела при той же температуре. ЗАКОН стефана- больцмана: M0=сигма T^4 сигма=5,7*10^-8 Вт/М^2*k^4 - постоаянная стефана больцмана. Энергетическая светимость абсолютно черого тела пропорциональна четвертой степени температуры на постоянную больцмана Закон смещения Вина. T λmax=b b=2,9*10^-3 мК Длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости абсолютно черного тела обратно пропорциональна его абсолютной температуре. λmax - длина волны на которую приходится максимум излучения!!!!!1 Постулат Планка 1) излучение электромагнитных волн атомами происходит отдельными порциями – квантами. Энергия кванта равна Э(эдс)=h НЮ h=6,62*10^-34 Дж*с – постоянная Планка M0лямбда=(2Pi*h*c^2/лямбда^5)*1/e^(hc/kTлямбда)-1 h- постоянная планка С- скорость света в вакууме k=1,38*10^-23 Дж/К - постоянная больцмана Абсолютно чёрное тело — физическое тело, которое при любой температуре поглощает всё падающее на него электромагнитное излучение во всех диапазонах. ... Спектр излучения абсолютно чёрного тела определяется только его температурой. 9 БИЛЕТ 1) третий закон ньютона. два тела взаимодействующие между собой всегда действуют на друг друга силами, векторы которых равны по модулю, противоположны по направлению и лежат на одной прямой. Примеры: 1) делая шаг мы действуем на землю силой, направленной вниз. От действия нашей силы участок земли под ступней деформируется, и возникающие в результате этого, упругие силы земли действуют на ступню вверх. Закон сохранения импульса: в замкнутой системе векторная сумма импульсов всех тел, входящих в систему остается постоянной при любых взаимодействиях тел этой системы между собой.
|