Механика. МЕХАНИКА. Механика механическое движение простейшая форма движения материи. Пространство и время. Система отсчета
 Скачать 27.56 Kb. Скачать 27.56 Kb.
|
|
МЕХАНИКА 1. Механическое движение – простейшая форма движения материи. Пространство и время. Система отсчета. Преставления о формах пространства и времени, лежащие в основе классической механики. Границы применимости классической механики. Простейшей формой движения материи является механическое движение, которое состоит в перемещении тел или их частей друг относительно друга. Совокупность тел, выделенная для рассмотрения, называется механической системой. Какие тела следует включить в систему, зависит от характера решаемой задачи. Если мы собираемся изучать движение какого-либо тела, то обязательно нужно указать, по отношению к каким другим телам происходит данное движение. Движение происходит как в пространстве, так и во времени (пространство и время — неотъемлемые формы существования материи). Поэтому для описания движения необходимо также определять время. Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образует систему отсчета. Описать движение тела означает указать для каждого момента времени положение в пространстве и скорость тела. Для того чтобы задать состояние механической системы, нужно указать положения и скорости всех тел, образующих систему. Тело, размерами которого в условиях данной задачи, можно пренебречь, называется материальной точкой. Абсолютно твердым телом называется тело, деформациями которого можно в условиях данной задачи пренебречь. Всякое движение твердого тела можно разложить на два основных вида движения — поступательное и вращательное. Пространство и время. Пространство — форма бытия материи (атрибут) со свойством протяжённости всех взаимодействующих во времени компонентов. (Компонент может являть собой как отдельный предмет (тело), так структуру и даже систему, в зависимости от функционального подхода к пространству.) Время. — форма бытия материи (атрибут) со свойствами длительности и последовательности смены состояний в пространстве. Все свойства пространства и времени неразрывны, взаимосвязаны с материальными образованиями (телами, предметами, структурами, системами), внутри и между которыми пребывают и развиваются те или иные формы движения. Существуют общие, а также особенные свойства пространства и времени. Общие свойства пространства: - объективность; - бесконечность; - взаимосвязь со временем и с движением; - зависимость от структурных характеристик материальных систем; - протяжённость; - единство прерывности и непрерывности: прерывность относительна по отношению к двум (или нескольким) взаимодействующим системам в пространстве; непрерывность — абсолютна, потому как пространство обладает связностью, в нём не может быть дискретности. Общие свойства времени: - объективность; - вечность; - взаимосвязь с пространством и с движением; - зависимость от структурных характеристик материальных систем; - единство прерывности и непрерывности: у времени нет естественных объективных перерывов, оно всеобъемлюще и течёт даже там, где могут образовываться пространственные пустоты, поэтому связный подход характерен для всех процессов и явлений во времени, так как они взаимосвязаны между собою потенциально и актуально: прошлое — настоящее — будущее. Особенные свойства пространства и времени: - для пространства — трёхмерность (высота-ширина-длина), симметрия и асимметрия, формы и размеры, местоположение, расстояние между предметами, распределение вещества, поля и космического вакуума; - для времени — одномерность, асимметричность, необратимость, то есть направленность всегда от прошлого к будущему, ритм процессов, скорость изменения состояния, неповторяемость, длительность. Система отсчета. Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которой рассматривается движение каких-либо тел. Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями: 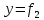 (t),z= (t),z=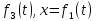 (1) (1)Где t – координаты определяющие положение тела x,у,z – декартовые координаты В современной физике любое движение считается относительным, и движение тела следует рассматривать лишь по отношению к какому-либо другому телу (телу отсчёта) или системе тел. Нельзя указать, например, как движется Луна вообще, можно лишь определить её движение, например, по отношению к Земле, Солнцу, звёздам и т. п. 2. Понятие материальной точки. Траектория, длина пути, вектор перемещения. Уравнение траектории. Материальная точка (частица) — простейшая физическая модель в механике — обладающее массой тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки. В классической механике масса материальной точки полагается постоянной во времени и не зависящей от каких-либо особенностей её движения и взаимодействия с другими телами. При аксиоматическом подходе к построению классической механики в качестве одной из аксиом принимается следующее: Материальная точка — геометрическая точка, которой поставлен в соответствие скаляр, называемый массой(r,m),r- вектор в евклидовом пространстве, отнесённом к какой-либо декартовой системе координат. Масса полагается постоянной, не зависящей ни от положения точки в пространстве, ни от времени. Траектория, длина пути, вектор перемещения. Число независимых координат, полностью определяющих положение точки в пространстве, называется число степеней свободы. Траектория – кривая, которую описывает радиус вектор материальной точки при её движении. В зависимости от формы траектории движение разделяется на - прямолинейное, - криволинейное. Расстояние, отсчитанное вдоль траектории, (длина участка траектории) называется длиной пути.S(t) - скалярная функция. Направленный отрезок прямой (вектор), соединяющий начальную и конечную точки траектории называется вектором перемещения (перемещением). При прямолинейном движении 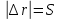 Если движение происходит в течение бесконечно малого времени Δt → 0, то по модулю путь равен перемещению dS= 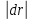 Уравнение траектории. Уравнение траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми. При движении точки с постоянным ускорением, которое описывает уравнение: r¯(t)=r¯0+v¯0t+a¯t2 (2) где r¯(t) - радиус-вектор точки в момент времени t; v¯0 - начальная скорость движения точки; a¯ - ускорение точки, траектория движения представляет собой плоскую кривую, что означает все точки этой кривой находятся в одной плоскости. Положение этой плоскости в пространстве задают векторы ускорения и начальной скорости. Ориентацию координатных осей чаще всего выбирают так, чтобы плоскость движения совпадала с одной из координатных плоскостей. В этом случае векторное уравнение (1) можно свести к двум скалярным уравнениям. Кинематическое описание движения материальной точки. Линия, которую описывает движущаяся материальная точка в пространстве, называют траекторией. В зависимости от формы траектории движения бывают прямолинейными и криволинейными. (Движение по окружности или по дуге окружности является простейшим случаем криволинейного движения.) Следует знать и помнить, что форма траектории данного движения материальной точки зависит от выбора системы отсчета и в этом смысле оказывается относительной. 3. Закон движения. Поступательное и вращательное движение – основные виды движений. Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки. В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида 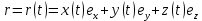 (3) (3)где r – радиус-вектор , характеризующий положение точки в момент времени t=0, v — вектор скорости материальной точки. Закон движения может быть найден, в зависимости от задачи, либо из дифференциальных законов механики (см. Законы Ньютона), либо из интегральных (см. Закон сохранения энергии, Закон сохранения импульса), либо из так называемых вариационных принципов. Поступательное и вращательное движение – основные виды движений. Поступательное движение — это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Сложное движение тела, состоящее из поступательного и вращательного движений. 4. Скорость и ускорение при криволинейном движении. Рассматривая криволинейное движение тела, мы увидим, что его скорость в разные моменты различна. Даже в том случае, когда модуль скорости не меняется, все же имеет место изменение направления скорости. В общем случае меняются и модуль и направление скорости. Таким образом, при криволинейном движении скорость непрерывно изменяется, так что это движение происходит с ускорением. Для определения этого ускорения (по модулю и направлению) требуется найти изменение скорости как вектора, т. е. найти приращение модуля скорости и изменение ее направления. 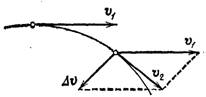 Рис. 1. Изменение скорости при криволинейном движении Пусть, например, точка, двигаясь криволинейно (рис.1), имела в некоторый момент скорость 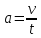 (4) (4)Где а- ускорение v— скорость тела t – время прошедшее с начала движения. По направлению Выбирая 5. Угловая скорость и угловое ускорение. Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Для вращения в двухмерном пространстве угловая скорость выражается числом, в трёхмерном пространстве представляется псевдовектором (аксиальным вектором), а в общем случае — кососимметрическим тензором. Угловая скорость характеризует скорость вращения тела и измеряется в радианах за секунду. 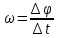 (5) (5)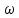 -угловая скорость -угловая скорость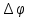 - угол поворота радиус-вектора - угол поворота радиус-вектора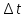 - промежуток времени - промежуток времениУгловое ускорение - псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени 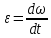 (6) (6)Где 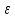 - ускорение - ускорение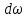 - псевдовекторная угловая скорость - псевдовекторная угловая скорость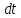 - псевдовектор времени - псевдовектор времениУгловое ускорение характеризует интенсивность изменения модуля и направления угловой скорости при движении твёрдого тела. |
